ДВИГАТЕЛИ

ВНУТРЕННЕГО

СГОРАНИЯ

Динамика

и конструирование

Под редакцией члена-корресповдента РАН, профессора, доктора технических наук В. Н. Луканина

Рекомендовано Государстве аным комитетом Российской Федерации по высшему образованию в качестве учебника для студентов высших учебных заведений, обучающихся по направлению «Наземные транспортные системы» и специальностям «Автомобиле- и тракторостроение», «Машины инженерного вооружения»

Москва «Высшая школа» 1995

Б1.К И. 365

Д23 УДК 621.43

Издание выпущено в свет при содействии Комитета РФ по печати

В. Н. Лукашш, И. В. Алексеев,

М. Г. Шатров, А. В. Павлов , Ю. В. Горшков,

Н. И. Назаров, С. П. Ежов, Л. М. Манохин, В. В. Сннявскин

Рецензенты:

кафедра «Поршневые и комбинированные двигатели» МГТУ им. Н. Э. Ба­умана (зав. кафедрой — д-р техн. наук, проф. Н. А. Иващенко); д-р техн.

наук, заслуженный деятель науки и техники РФ, проф. В. И. Крутов

Двигатели внутреннего сгорания. В 3 кн. Кн. 2. Дииами- Д23 ка и конструирование: Учеб./В. Н. Лукаяин, И. В. Алексеев, М. Г..Шатров и др.; Под ред. В. Н. Луканина. — М.: Высш. шт., 1995 — 319 с.: нл.

ISBN 5-06-003298-1

ISBN 5-06-003296-5 (Кн. 2)

В книге содержатся сведения по кинематике и динамике кривошипно- шатунного механизма, излагаются вопросы уравновешивания, колебаний, шу- ма и ввбраши ДВС и их элементов; проведен анализ условий работы, особен- ностей конструкции, расчета деталей и систем ДВС; рассмотрены основы проектирования ДВС с использованием ЭВМ.

Для студентов технических вузов и специалистов.

2203050000—090

Д ■ 82—95

001(01)—«5

ББК 31.363 6П2.24

ISBN 5-06-003298-1 ISBN 5-06-003296-5 (Кн. 2)

© Коллектив авторов, 1993

ПРЕДИСЛОВИЕ

Настоящая книга является второй частью учебника do двига­телям внутреннего сгорания, включающей разделы, касающиеся кинематики, динамики, основ конструирования и расчета элементов и систем ДВС.

Основу приведенного в книге учебного материала составляют лекционные курсы, читаемые членами авторского коллектива в МА- ДИ (ТУ) для студентов, обучающихся по направлению «Наземные транспортные системы», и по объему и содержанию соответст­вующие их учебным планам и программам.

Учебник может быть использован также студентами высших учебных заведений, обучающихся по направлению «Энергомашино­строение», специальности «Двигатели внутреннего сгорания»; по направлению «Технологические машины и оборудование», специ­альности «Подъемно-транспортные, строительные, дорожные ма­шины и оборудование»; по направлению «Эксплуатация транспорт-. ных средств» и специальностям «Организация дорожного движе­ния», «Сервис и техническая эксплуатация транспортных и тех­нологических машин и оборудования» (автомобильный транспорт; строительное, дорожное и коммунальное машиностроение); по на­правлению «Наземные транспортные системы» и специальностям «Автомобиле- и тракторостроение», «Автомобили и автомобильное хозяйство», «Машины инженерного вооружения».

Методика изложения материала отдельных разделов максима­льно адаптирована к современным способам анализа работоспособ­ности, а также термической и динамической нагруженности элемен­тов двигателя с использованием ЭВМ.

В учебный материал включены новейшие достижения в констру­ировании двигателей, используемых в средствах наземного транспо­рта, нх элементов и систем, а также описаны современные тех­нологии их производства, эксплуатации и ремонта.

Отдельные разделы написали:

В. Н. Луканин - предисловие, § 1.3, гл. 16 (совместно с А. В. Павловым); И. В. Алексеев — гл. 2, 8; М. Г. Шатров — § 1.1, 1.2, гл. 4, 5, § 9.3; А. В. Павлов — гл. 7, 10, 14; Ю. В. Горш­ков — гл. 6, 11, § 9.1, 9.2; Н. И. Назаров — гл. 3,15; С. П. Ежов — § 12.1, 13.1; Л. М. Матюхмн — § 13.2; В. В. Синявский — § 12.2.

з

Авторский коллектив выражает искреннюю благодарность ре­цензентам д-ру техн. наук, проф. В. И. Крутову и коллективу кафе­дры «Поршневые и комбинированные двигатели» МГТУ им.

Н. Э. Баумана (зав. кафедрой — д-р техн. наук, проф. Н. А. Ива­щенко) за принципиальное и доброжелательное рецензирование ру­кописи. Их замечания во многом способствовали улучшению каче­ства учебника.

Авторы

Глава 1 кинематика и динамика кривошипно-шатунного механизма

1. КИНЕМАТИКА KIUM

В автотракторных ДВС в основном используются следующие три типа кривошипно-шатунного механизма (КШМ): центральный (аксиальный), смещенный (дезаксиальный) и механизм с прицепным шатуном (рис. 1.1). Комбинируя данные схемы, можно сформиро­вать КШМ как линейного, так и многорядного многоцилиндрового

Реализация смещенного (цезаксиального) механизма возможна в двух вариантах. В первом случае ось цилиндра не пересекает ось коленчатого вала ДВС, а во втором — ось поршневого пальца смещается относительно оси цилиндра.

КШМ с прицепным шатуном отличается от других схем наличи­ем прицепного шатуна, соединенного пальцем с главным шатуном в его кривошипной головке. Необходимо отметить, что кинематика механизма главного шатуна не отличается от кинематики централь­ного и смещенного КШМ.

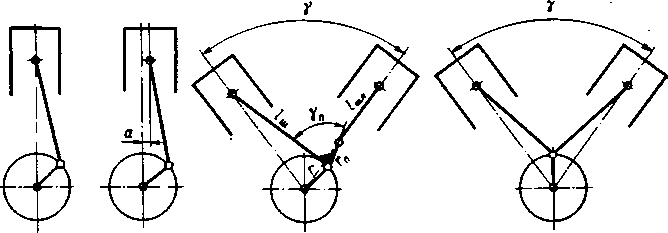
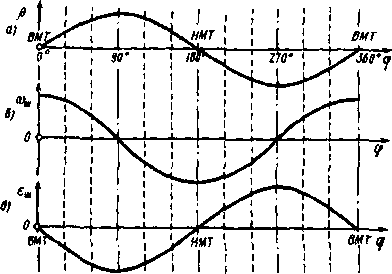
Рис. 1.1. Кинематические схемы КШМ: а — цевтральвм линейная. 6 — смешанная линейная, « — прицепная, г — цмтряльвм

V-образвая

две.

в)

5

Изучение законов движения деталей КШМ проводится с учетом только его структуры и геометрических соотношений между звенья- ми механизма независимо от сил, вызывающих его движение, и сил трения, при отсутствии зазоров между сопряженными элементами и постоянной угловой скорости кривошипа.

При работе ДВС основные элементы КШМ совершают различ- ные виды перемещений.

Поршень движется возвратно-поступательно. Шатун совершает сложное шюскопараллельное движение в плоскости его качания. Кривошип коленчатого вала совершает вращательное движение относительно его оси.

1. КИНЕМАТИКА ЦЕНТРАЛЬНОГО КРИВОШИПНО-ШАТУННОГО;

МЕХАНИЗМА

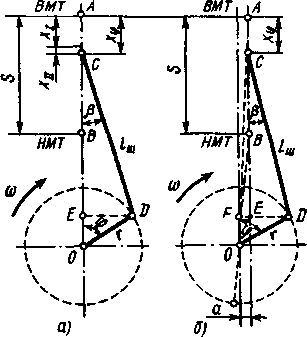
Расчетная кинематическая схема КШМ представлена на рис. 1.2.

Основными геометрическими параметрами, определяющими за- коны движения элементов центрального КШМ, являются: г — радиус кривошипа коленчатого вала, /_ш — длина шатуна.

Параметр А=г//_Ш является критерием кинематического подобия центрального механизма. При этом для КШМ различных размеров, но с одинаковыми Я законы движения аналогичных элементов по- добны. В автотракторных ДВС применяют КШМ с А = 0,24...0,31.

В смещенных (дезаксиальных) КШМ имеется еще один геомет- рический параметр, влияющий на его кинематику, — величина сме- щения оси цилиндра (пальца) относительно оси коленчатого вала (а). При этом относительное смещение k = ajr является дополни-

тельным к А критерием кинемати- ческого подобия смещенных КШМ. Таким образом, подобные смещенные КШМ имеют одина- ковые Ли к, где к изменяется в пределах 0,02...0,1.

Как следует из схемы (рис. 1.2), кинематика КШМ полно- стью описывается, если известны законы изменения по времени следующих параметров:

ф перемещения поршня (*)■ Начало отсчета (л = 0) — положе- ние поршня в ВМТ; положитель- ное направление отсчета принято при его движении от ВМТ к НМТ при вращении кривошипа по ча- совой стрелке;

0 угла поворота кривошипа

Рис. 1.2. Расчетные схемы КШМ: а — певтральвого, 6 — смещенного

6

(<р). Начало отсчета — положение кривошипа при нахождении поршня в ВМТ;

ф угла отклонения шатуна (fi) от оси цилиндра (/5 = 0 при <р = 0).

Л Кинематика кривошипа. Вращательное движение кривошипа коленчатого вала определено, если известны зависимости угла по- ворота (q>), угловой скорости (ю) и ускорения (е) от времени (*)■

При кинематическом анализе КШМ принято делать допущение о постоянстве угловой скорости (частоты вращения) коленчатого вала (ш). Тогда ш —const и е = 0. Угловая скорость и частота

вращения кривошипа (и) коленчатого вала связаны соотношением ш=лп/ЗО. Данное допущение позволяет изучать законы движения элементов КШМ в более простом виде в функции угла поворота кривошипа, переходя при необходимости к временной форме, ис- пользуя линейную связь между <р и I.

А Кинематика поршня. Кинематика возвратно-поступательно движущегося поршня описывается зависимостями его перемещения (хД скорости (v_v) и ускорения (j_v) в функции угла поворота криво- шипа (<р).

• Перемещение поршня при повороте кривошипа на угол <р определяется как сумма его смещений от поворота кривошипа на угол <р (Х)) и от отклонения шатуна на угол fi (дс_а):

х=г+1_ш—г со$<р — /_ш cosjJ, или окончательно с учетом X = г\1_ш

x—t [(1—cos <р)+(1/А) (1—cos/?)]. (1.1)

Связь между углами <р и fi определяется по общей стороне DE треугольников ODE и CDE (рис. 1.2, а), откуда для центрального механизма г sin <р = /_ш sin fi или A sin <р = sin fi, а для смещенного, опре- делив DE как г sin (р—а — l_m sin fi, X (sin <р — к) = sin fi. Используя дан- ное соотношение, а также учитывая, что соsfi — ^l —sin² fi, получим зависимость перемещения поршня от угла поворота кривошипа.

Для центрального КШМ это

x = r [(l-cos<p) + (l/X) {\-yJ\-X²sia²(p)l (1.2)

В смещенном КШМ

I

х—

cos б—cos©

X

(1.3)

С целью упрощения расчетных зависимостей для центрального КШМ разложим в ряд по формуле бинома Ньютона радикал

у/\ — A² sin² <р:

1

•y/l — Я ² sin²<p= 1 — - (Яsin<p)² — - (Asin^j)*—- (Asinp)* —

2. 8 16

—— Usin<j[>)⁸ + ... .

128

При Я = 0,25 амплитуды при гармонических членах разложения соотносятся как 1; 0,031:0,000488:0,000015, а при Я = 0,30 — как 1:0,045:0,001012:0,000046. С учетом этого с достаточной для прак- тики точностью можно ограничиться двумя первыми членами раз- ложения и полагать

-t/l — A²sin²9«l— ^ A²sin²<p= 1—^ к^гcos2<p.

Тогда

x^r [(1— cos^) + (A/4) (1 — cos2ф)] = Х1+^п. (1.4)

Ф Скорость поршня определяется как первая производная от перемещения поршня по времени, т. е.

^7=??' <‘-⁵>

dr d<p d(

что применительно к уравнениям (1.1) и (1.4) дает точную

и приближенную

кт (ю+Д

v^rco—(1.6)

СО$Р

vc*r<o [sin (р + (Я/2) sin 2<р] (1.7)

зависимости скорости поршня от угла поворота кривошипа.

Как видно из (1.6), максимального значения скорость достигает при ф+0 = 9О°, когда sin (<р + /?) = 1. При этом ось шатуна перпен­дикулярна радиусу кривошипа и

v_mu = roi*/l+I*. (1.8)

Широко применяемая для оценки конструкции ДВС средняя ско­рость поршня, которая определяется как c_a=Snj3Q, связана с мак­симальной скоростью поршня соотношением v_mujc₀=*-уЛ +Я² и

для используемых Я равна 1,62... 1,64.

0 Ускорение поршня определяется производной от скорости поршня по времени, что соответствует точно

Гею (р+Д) cos¹ «Л

_;=гш + *—- I (1.9)

[_ cos fi COS³/?J

Рис. 1.3. Кинематические параметры поршня: а — перемещение, 6 — скорость, « —- ускорение

и приближенно

у~гш² (cos gj + Я cos 2<р).

(1.10)

В современных ДВС j=5000...20 000 м/с².

Максимальное значение Ли* = га>² (1+А) имеет место при <р = 0 и 360 град ПКВ. Угол <р= 180 град ПКВ для А<0,25 соответствует минимальному значению ускорения jmu= —го² (1 —А). Если А >0,25,

180° +

то имеется еще два экстремума j'=— rw² ^А+^ при <р’ =

arcco.s _ti л

Графическая интерпретация уравнений перемещения, скорости и ускорения поршня приведены на рис. 1.3.

Для дезаксиального КШМ приближенные значения v и j имеют вид

v~ro) [sin (р + (А/2) sin 2(р — kX cos <f>], j~ra)² (cos (p + X cos 2<p+kX sin a).

Сравнивая эти зависимости, а также (1.3) с аналогичными для центрального КШМ, можно отметить их отличие в добавочном члене, пропорциональном кХ. Так как для современных двигателей £А-0,01...0,05, то его влияние на кинематику механизма невелико и на практике им обычно принебрегают.

А Кинематика шатуна. Сложное плоскопараллельное движение шатуна складывается из движения его верхней головки с кинемати­ческими параметрами поршня и его нижней кривошипной головки с параметрами конца кривошипа.

Кроме того, шатун совершает вращательное (качательное) дви­жение относительно точки сочленения шатуна с поршнем.

9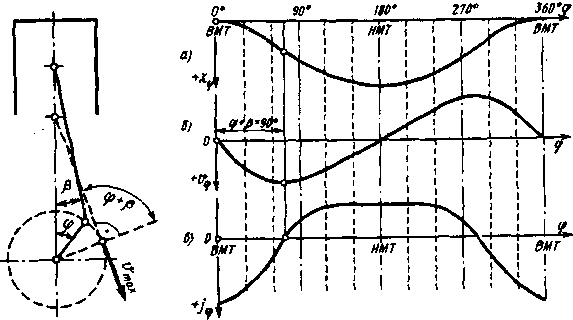

Рис. 1.4. Кинематические параметры шагуяа: а — перемещение, б — скорость, « — ускорение

• Угловое перемещение шатуна /J = arcsin (A sin q>). Экстремальные значения /? = +arcsin А имеют место при <р = 90

и 270 град ПКВ. В автотракторных двигателях 0_т«= ±(12...18°). ф Угловая скорость качания шатуна

dfim 1

ш_ш=-— или <х>_ш = Аш .

4l COSjSm

Экстремальные значения <Ут= ±Аш наблюдаются при и 180 град ПКВ.

• Угловое ускорение шатуна

<3а>_ш di%, d(f> dtu_m , .

е_ш=-—= =а> —= Aar sm <p

d( dip di dtp

A²-I

,3/2

(1 —/1*8Ш^Л 4?)

Экстремальные значения е_ш= ±Aca²/_v/l достигаются при

<р = 90 и 270 град ПКВ.

Изменение кинематических параметров шатуна по углу поворо­та коленчатого вала представлено на рис. 1.4.

2. ДИНАМИКА КШМ

При работе двигателя в КШМ действуют следующие основные силовые факторы: силы давления газов, силы инерции движущихся масс механизма, силы трения и момент полезного сопротивления. При динамическом анализе КШМ силами трения обычно пренеб­регают.

10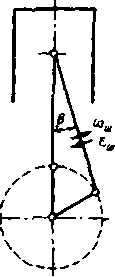

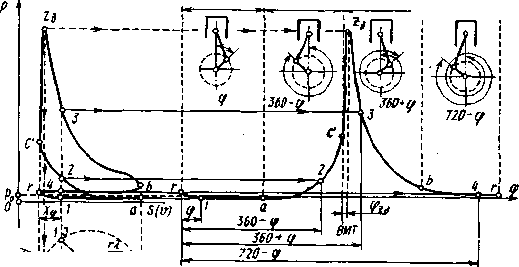
Впуск

C*amut PaceiuptHUt выпуск

— *

t«-

•

^a

ч> .

Z?-“—'

Ряс. 1.5. Перестроение индикаторной диаграммы вз p-V- в р-<р- координа­ты

1. СИЛЫ ДАВЛЕНИЯ ГАЗОВ

Сила давления газов возникает в результате осуществления в ци- линдрах рабочего цикла. Эта сила действует на поршень, и ее значение определяется как произведение перепада давления на по- ршне на его площадь: Р_т—(Рг—Ро) Здесь р_т — давление в цилиндре двигателя над пор- _Р-

Л1к:м, р_а ■ давление в картере, F_u — пло- щадь поршня.

Для оценки динамической нагруженности элементов КШМ важное значение имеет зави- симость силы Р_г от времени. Ее обычно полу- чают перестроением индикаторной диаграм- мы из координат р — V в координаты р — <р посредством определения V_v=x^F_n с исполь- зованием зависимости (1.1) или графических методов (рис. 1.5).

Сила давления газов, действующая на по- ршень, нагружает подвижные элементы КШМ, передается на коренные опоры картера н уравновешивается внутри двигателя за счет упругой деформации несущих элементов блок-картера силой Р_г и /У, действующей на головку цилиндра, как это показано на рис.

1.6. Эти силы не передаются на опоры двига- теля и не вызывают его неуравновешенности.

Рис. 1.6. Воздействие газовых сил на. элемен­ты конструкции КШМ

11

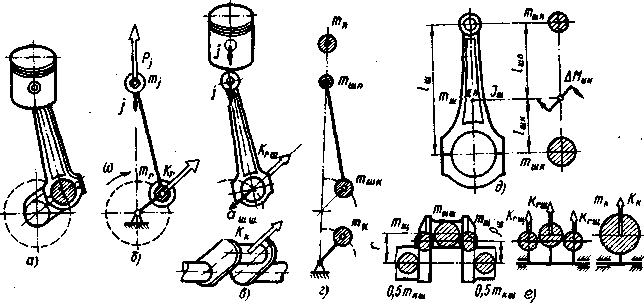
1.2.1 СИЛЫ ИНЕРЦИИ ДВИЖУЩИХСЯ МАСС КШМ

Реальный КШМ в общем случае представляет собой систему с распределенными параметрами, элементы которой движутся нера­вномерно, что приводит к возникновению инерционных нагрузок.

Детальный анализ динамики такой системы принципиально воз­можен, однако сопряжен с большим объемом вычислений.

В связи с этим в инженерной практике для анализа динамики ДВС широко используют модели с сосредоточенными парамет­рами, созданные на основе метода замещающих масс. Они форми­руются из масс, сосредоточенных в выбранных по определенным правилам точхах КШМ, которые связаны между собой абсолютно жесткими безынерционными элементами. Замещающие точки опре­деляют с учетом конфигурации и характера движения отдельных элементов звеньев КШМ н выбираются обычно в местах сопряже­ния кинематических пар. При этом для любого момента времени должна выполняться динамическая эквивалентность модели и рас­сматриваемой реальной системы, что обеспечивается равенством их кинетических энергий.

В ДВС для анализа динамики его КШМ обычно используют двухмассовую модель (рис. 1.7). Первая замещающая масса ntj со­средоточена в точке сопряжения поршня с шатуном и совершает возвратно-поступательное движение с кинематическими парамет­рами поршня, вторая т, располагается в точке сопряжения шатуна с кривошипом и вращается равномерно с угловой частотой со. Вели­чины масс nij и т_г должны выбираться из условия обеспечения эквивалентности модели и замещаемого ею механизма.

• Детали поршневой группы совершают прямолинейное возврат­но-поступательное движение вдоль оси цилиндра. Так как центр

Ряс. 1.7. Формирование двухмассовой динамической модели КШМ: а — КШМ, б — модель КШМ, « — шы в КШМ, г — массы КШМ, д — массы шатуна,

е — массы кривошипа

12

масс поршневой группы практически совпадает с осью поршневого пальца, то для определения силы инерции достаточно знать массу поршневой группы т_ш которую можно сосредоточить в дан­ной точке, и ускорение центра масс /, которое равно ускорению поршня Pja= —mj.

1# Кривошип коленчатого вала совершает равномерное враща­тельное движение. Конструктивно он состоит из совокупности двух половин коренной шейки, двух щек и шатунной шейки. При равно­мерном вращении на каждый из указанных элементов кривошипа действует центробежная сила, пропорциональная его массе и цент­ростремительному ускорению. С учетом того, что центры масс ко­ренных шеек кривошиаа находятся на оси вращения, их центробеж­ные силы инерции равны нулю. Центр масс шатунной шейки рас* положен на ее оси, отстоящей от оси коленчатого вала на рас­стоянии г. Центростремительное ускорение шейки равно a_IBS=m)^z. Полагая массу шатунной шейки сосредоточенной в ее центре масс, получим выражение, определяющее центробежную силу: К_гша= —т_шжгт^г. Аналогично, по известным массе щеки т_щ и рас­стоянию от оси коленчатого вала до центра ее масс р_щ, определяют­ся центростремительное ускорение центра масс а_т=р_ш(о² а соответ­ственно центробежная сила инерции Кгщ= ~тщр_та> .

В эквивалентной модели кривошип заменяют массой от*, отстоя­щей от оси вращения на расстоянии г. Величину массы определя­ют из условия равенства создаваемой его центробежной силы сумме центробежных сил масс элементов кривошипа: Я_Ж = А_ЛИШ+2Х_ГЩ или т_хго)²=т_шшга>¹+2т_шр_ша)², откуда после преобразований получим Гог=Ющш+2т_шр_ш1г.

Ф Элементы шатунной группы совершают сложное плоскопа- раллельное движение. В двухмассовой модели КШМ массу шатун- ной группы разделяют на две замещающие массы: п^ш, сосре­доточенную на оси поршневого пальца, и т^, отнесенную к оси шатунной шейки коленчатого вала. В этом случае для приведения всех ее сил инерции к результирующим силам принципы метода замещающих точек сводятся к выполнению следующих условий:

1. сумма масс, сосредоточенных в замещающих точках модели, должна быть равна массе замещаемого звена КШМ. Применитель­но к группе шатуна т_ши + т_ш = т_ш;

2. положение центра масс элемента реального КШМ и замеща­

ющего его в модели должно быть неизменным. Обозначим рассто­яния от центров поршневой и кривошипной головок шатуна до его центра масс как 4ш и /щ*. Условие неизменности положения центра масс выполняется, если —/Пш,4ш = 0- Из приведенных в п. 1 и

2 соотношений следует, что m_IBn=fnJuJlm и m_aa=m_sJ_aJi_va.

Выполнение первых двух условий обеспечивает статическую эк­вивалентность замещающей системы реальному КШМ;

3. условие динамической эквивалентности замещающей модели

13

обеспечивается при равенстве суммы моментов инерции масс, рас­положенных в характерных точках модели У*,, и момента инерции реального шатуна У_ш относительно оси, проходящей через ценгр масс звена перпендикулярно плоскости его качания. Данное условие для двухмассовых моделей шатунов существующих ДВС обычно не выполняется, что может быть скомпенсировано добавлением к си­стеме инерционного момента ДМ_Ш — 7„~У_Э„.

Статистические данные по рассмотренным параметрам КШМ современных автотракторных двигателей представлены в табл. 1.1 в виде конструктивных масс m'=mJF_a, где — площадь поршня, т — масса соответствующего элемента КШМ.

Окончательно, объединив полученные массы всех звеньев КШМ в замещающих точках динамической модели КШМ, получим:

Ф массу, сосредоточенную на оси пальца и совершающую воз- вратно-поступательное движение вдоль оси цилиндра,

ф массу, расположенную на оси шатунной шейки и соверша­ющую вращательное движение вокруг оси коленчатого вала, т_г=т₁4-т_[ш:. Для V-образных ДВС с двумя шатунами, расположен­ными на одной шатунной шейке коленчатого вала, т,=т_г + 2т_ак.

В соответствии с принятой моделью КШМ первая замещающая масса тр движущаяся неравномерно с кинематическими парамет­рами поршня, вызывает силу инерции Pj= —m_}j, а вторая масса т, вращается равномерно с угловой скоростью кривошипа и создает центробежную силу инерции К_г= —Ощ^Пг.

4

Рис. 1.8. Воздействие сил инерции на опоры двигателя: а — «яя» Pj, 6 — <жл* К,

14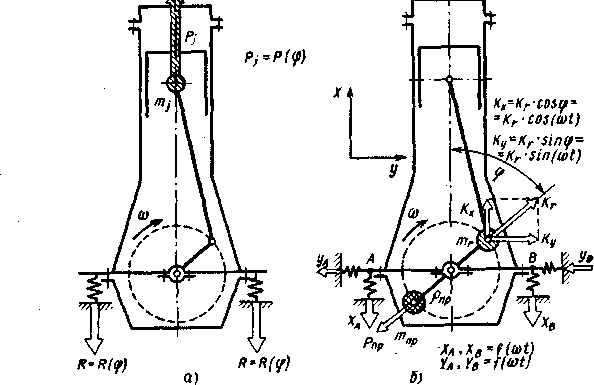

Таблица LI

Тип двигателя	Частота вращения, мин-1	Конструктивная масса т', жг/м1		Отношение Lirllm
		поршневой группы	шатуна	линейные	V-обраэяые
Д^ига- теЛя с ис­кровым зажига­нием	л <4500 я>4500	(1,2...U)Z>* (1,3...1,4) D	М,5...1,6> D (1,9...2,2) D	0,26...0,28 0,26... 0,28	0,28...0,30 0,28...0,30
Дизели автомо- бильяые	жЗООО «>3000	(2,0...2,2) D (1,7...1,9) D	(2,3...2,5) D (1,8...2,1) D	0,2б...0,30 0,22-0,23	0,30...0,34 0,22.-0,23
Дизели трактор­ ные	—	(2,2...2,4) D	(2,5...2,8) D	0,26. ..0,30	0,30—0,34

* D — диаметр цилиндра, мм.

Сила инерции Р_} уравновешивается реакциями опор, на которые установлен двигатель. Будучи переменной по значению и направле­нию, она, если не предусмотреть специальных мероприятий по ее уравновешиванию, может быть причиной внешней неуравновешен­ности двигателя, как это показано на рис. 1.8, а.

При анализе динамики и особенно уравновешенности ДВС с уче­том полученной ранее зависимости ускорения j от угла поворота кривошипа (Ф) Pj представляют в виде суммы сил инерции первого (Р,0 и второго {Pju) порядка:

Pj^ —mjra>^г (cos<p+Хcos2<р) = Ceos<р + ХСcos2(p = Pj\ + Pjv, где С = —ntjro)¹.

Центробежная сила инерции К,= —т/а¹ от вращающихся масс КШМ представляет собой постоянный по величине вектор, направ­ленный по радиусу кривошипа и вращающийся с постоянной уг­ловой частотой (а. Сипа К_г передается на опоры двигателя, вызывая переменные по величине реакции (рис. 1.8, б). Таким образом, сила К_п как и сила Р_ь может являться причиной внешней неуравновешен­ности ДВС.

3. СУММАРНЫЕ СИЛЫ И МОМЕНТЫ, ДЕЙСТВУЮЩИЕ В КШМ

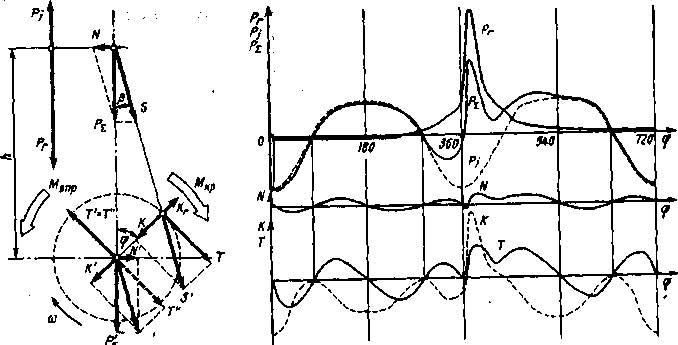
При динамическом анализе КШМ силы Р_г и Pj, имеющие общую точку приложения к системе и единую линию действия, заменяют суммарной силой, являющейся их алгебраической суммой: P_z = = P_T+Pj (рис. 1.9, а).

15

Для анализа действия силы <P_L на элементы КШМ ее расклад*^ вают на две составляющие: S и N. Сила S действует вдоль ом шатуна и вызывает повторно-переменное сжатие — растяжение егс элементов, а сила JV перпендикулярна оси цилиндра и прижимав поршень к его зеркалу. Действие силы S на сопряжение шатун*— кривошип можно оценить, переыеся ее вдоль оси шатуна в точку ш шарнирного сочленения, где она раскладывается на нормаль ну к силу К, направленную по оси кривошипа, и тангенциальную сил/ Т

Силы К и Т передаются на коренные опоры двигателя. Дл* анализа их действия данные силы переносятся в центр коренной опоры, чему соответствуют силы К', Т и V на рис. 1.9, а. Пара сиг Г и Г на плече г создает крутящий момент М^, который дале< передается на маховик, где совершает полезную работу. Сумма сил К' и Т" дает силу S”, которая, в свою очередь, раскладывается га две составляющие: N' и Р_г\ Очевидно, что N= — N' и Pz — Pe- Сили N и N' на плече h создают опрокидывающий момент M_OBV=Nh который далее передается на опоры двигателя и их реакциям* уравновешивается. и вызываемые им реакции опор изменяются по времена и могут быть причиной внешней неуравновешенное™ двигателя.

Основные соотношения для рассмотренных сил и моментов:

Рис. 1.9. Силы в КШМ: а — расчетная схема, 6 — эаявсимосгь сел в КШМ от угла поворота голеичатого вала

PI'S'

а)

16

sin (<p+0) .. _

Г-Л——7-, M^=Tr.

cos p

Mrap= -Nh= (InCOSp+rCOSCp)-

sir. {<p +$)

• —Ptf——~^~= ~Tr= —Мц,

cosp

3. СИЛЫ, ДЕЙСТВУЮЩИЕ НА ШЕЙКИ КОЛЕНЧАТОГО ВАЛА

9 Силы, действующие на шатунную шейку коленча­того вала. На шатунную шейку кривошипа действуют сила S', направленная по оси шатуна, а также центробежная сила К^, действующая по радиусу кривошипа (рис. 1.10). Результирующая сила Ддш, нагружающая шатунную шейку, определяется как век­торная сумма этих двух сил. Ее зависимость от угла поворота коленчатого вала (<р) может быть представлена в виде полярной диаграммы нагрузки на шатунную шейку (ПДНШШ), которая является геометрическим местом точек конца радиуса-вектора Ящш, ориентированного относительно системы координат, связанной с кривошипом. При этом кривошип условно полагается неподвиж­ным, а ось цилиндра вращается в противоположную сторону с той

Рис. 1.10. К расчету сия, нагружающих шатунную шейку: а — рясчетна* схема, б — построение ПДНШШ, * — ПДНШШ, г — теоретическая диа­грамма износа шатунной шебхн

11

же угловой скоростью. Такое представление не изменяет взаимного расположения элементов КШМ и, следовательно, значения и ори­ентацию относительно них действующих сил. Так как при непод­вижном кривошипе ориентация сил К., Т и однозначно н просто

определяется взаимным расположением шатуна и кривошипа,, то процесс построения диаграммы сил R^m в этом случае легко Фор­мализуется и построение векторной диаграммы сил R_uзначитель­но упрощается,

ТТДНТПШ дает наглядное представление о значении и направле­нии действия относительно кривошипа силы, нагружающей в дан­ный момент шатунную шейку, и об условной точке ее приложения.

Зависимость модуля силы Лцщ, от угла поворота, построенная в прямоугольных координатах R^ — <р, далее используется для рас­чета шатунного подшипника.

С учетом изложенного выше метод построения ГГДНШШ сво­дится к следующему. В прямоугольных координатах из полюса О (рис. 1.10,6), который соответствует центру шатунной шейки, для каждого угла поворота до значениям сил К₉ и Т_ф строят силу S_g. Концы этого вектора последовательно соединяют плавной кривои, в результате чего получают полярную диаграмму данной силы. Затем к точке О вдоль оси К прикладывают вектор центробежной силы от части массы шатуна, приведенной к кривошипу К_т. Вектор, проведенный из точки 0_ШЗ представляющей начало вектора в точку, соответствующую концу вектора S, является результиру­ющей силой Лщп. Совокупность этих точек ПДНШШ относительно полюса О_щ позволяет получить значение и ориентацию силы К,™* к поверхности шейки для любого значения угла поворота колен­чатого вала.

ПДИШШ V-образного двигателя определяемся типом соедине­ния шатунов с коленчатым валом. Для двигателя с шатунами, расположенными рядом на одной шатунной шейке, результиру­ющие силы, нагружающие соответствующие участки шейки для каждого из шатунов, определяются отдельно, аналогично тому, как это выполнялось в случае линейного двигателя. В ПДНШШ V- образного двигателя с сочлененными шатунами результирующая сила Лцщ,, нагружающая шатунную шейку, определяется попарным суммированием векторов ЪК и ЪТ, одновременно передаваемым на шейку со стороны цилиндров левого и правого рядов. Здесь = и 2,Т~Т_Л+Т_а. Затем после определения их результирую­

щей они суммируются с вектором

• Силы, нагружающие коренные шейки коленчатого вала. Коренные шейки кривошипа одноцилиндрового двигателя нагружаются силой Дпш = •?+и центробежной силой инерции масс кривошипа (рис. 1.11). Их результирующая сила Д, = л,аш + + £г, действующая на кривошип, воспринимается двумя коренными опорами. Поэтому сила, действующая на каждую коренную шейку, равна

18

Рис. 1.11. Построение полярной диаграммы нагрузки на коренную шейку (шестая коренная шейка шесгицилиндрового четырехтактного двигателя)

половине результирующей силы & и направлена в противополож­ную сторону:

R_tiB=-0,5R,= -0,5 (£+£* + £)= -0,5 (S+R,), где R_r=&*■

Формально нагрузка на коренную шейку в одноцилиндровом двигателе может быть определена для любого значения угла пово­рота кривошипа с использованием ПДНШШ, если ее полюс перене­сти из точки О_т в точку 0_It положение которой определяется ве­личиной отрезка О_тО_х = \К,\. В этом случае отрезок ОО_х представля­ет собой модуль суммы векторов и R_t. Уменьшив масштаб сил в два раза и изменив ориентацию исходной полярной диаграммы R_x на противоположную, получим искомую полярную диаграмму нагрузки на коренную шейку (ПДНКШ).

Влияние противовеса на коренную шейку можно учесть, прило­жив его инерционную результирующую силу Лщ, к точке О,.

Нагрузки на коренную шейку многоцилиндрового двигателя можно получить, представив его в виде совокупности одноцилинд­ровых двигателей, кривошипы которых вращаются синхронно и по­вернуты друг относительно друга на угол 6, определяемый ком­поновочной схемой коленчатого вала. В этом случае резулътирую-

19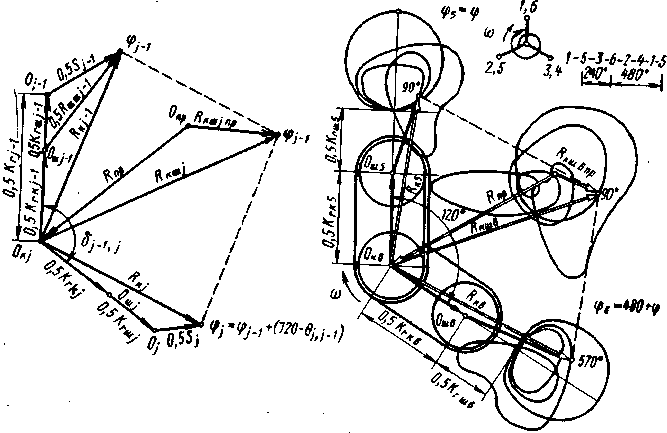

зд lid тта m m да m .. . Лу протвэНеш . ~— £ ярдтиШеСйти

Рис. 1.12.Дяаграмма вагруэож на кореануто шейку

щая сила нагружающая j-ю коренную опору, получается сум­

мированием векторов от двух смежных кривошипов: R*щг= =л"ия>_| +Л'п^, — действующих на коренные шейки в один и тот же момент времени. Идентификация векторов, действующих одно­моментно на отдельных кривошипах, проводится с учетом порядка работы цилиндров. Связь соответствующих углов поворота криво­шипа вычисляется со выражению <р_}~<р^1+(120—в₁₎_₁), где fyj-i — угол запаздывания работы j-го цилиндра относительно (j— 1 )-го.

На рис. 1.11 дан пример построения полярной диаграммы на­грузки на шестую коренную шейку шестицилиндрового линейного двигателя. Для этого ПДНКШ от пятого и шестого кривошипов ориентируют друг относительно друга в соответствии с их взаим­ным расположением на коленчатом валу (в данном случае под уг­лом д—120°). Полюсы О_к обеих диаграмм совмещают. Затем про из- водят попарно геометрическое суммирование векторов и R^f. Отсчет углов в полученной ПДНКШ ведут по левому кривошипу.

Влияние противовесов на нагружениосгь коренной шейки пока­зано на рис. 1.12.

3. ТЕОРЕТИЧЕСКАЯ ДИАГРАММА ИЗНОСА ШЕЕК ВАЛА

С использованием полярных диаграмм строят теоретическую Диаграмму износа шейки вала (ТДИШВ). С ее помощью можно обоснованно наметить место на поверхности шейки, где целесооб­разно расположить выход М поверхность маслоподводящего кана­ла. Построение ТДИШВ ведется при следующих допущениях:

0. величина износа шейки пропорциональна действующей на нее силе;

20

• износ равномерно распределен в обе стороны от условной точки приложения силы на дугах в 60°, что соответствует зоне контакта вала и подшипника в пределах дуги 120°;

• коррозионный и эрозионный износ шеек отсутствует.

Для построения ТДИШВ можно принять такую последователь­ность действий (см. рис. 1.10, в, г).

1. На поверхность шейки, изображенной в произвольном масш­табе, плоскопараллельно с полярной диаграммы переносят силы Лцш,, полученные через равные угловые интервалы поворота колен­чатого вала, кратные 360° (например, 30°), так, чтобы силы были направлены к центру шейки.

2. На шейке выделяют сектор в 120°, ориентированный своей дугой вниз с биссектрисой угла, совпадающей с вертикальной осью кривошипа.

3. Производят суммирование всех сил попавших в данный сехтор. С учетом принятых допущений износ в пределах данного сектора будет равномерным и по величине пропорциональным по­лученной сумме сил.

4. В принятом масштабе (так, чтобы сумма сил для наглядности составляла приблизительно 1 /3 радиуса шейки) на биссектрисе угла сектора откладывают отрезок, пропорциональный износу, от на­ружной поверхности к центру окружности шейки.

5. Затем выделяют следующий сектор, повернутый относитель­но предыдущего на фиксированный угол, соответствующий приня­тому углу дискретизации Диш (в нашем примере 30°), и повторяют операции 3 и 4. Данные действия производят последовательно до тех пор, пока интервал дискретизации не перекроет всю окружиость шейки.

6. Полученные точки, характеризующие износ, соединяют плав­ной кривой.

7. На основании сформированной кривой выбирают ось масло­подводящего канала так, чтобы она находилась в зоне с минималь­ным износом, что соответствует минимальному удельному давле­нию между подшипником и шейкой. Именно в этой зоне возможно наименьшее перекрытие канала поверхностью подшипника. Необ­ходимо отметить, что ТДИШВ позволяет лишь качественно опи­сать характер износа шейки. При выборе рационального места расположения отверстия для масла на шейке следует также учиты­вать и факторы, влияющие на ее прочность.

3. СУММАРНЫЙ КРУТЯЩИЙ МОМЕНТ ДВИГАТЕЛЯ

Ф Моменты, скручивающие коренные шейки многоци­линдрового двигателя. В одноцилиндровом двигателе крутя­щий момент М_1? = Тг. Так как г — величина постоянная, то харак­

21

тер его изменения по углу поворота кривошипа полностью опреде­ляется изменением тангенциальной силы Т.

Представим многоцилиндровый двигатель как совокупность

1. одноцилиндровых, рабочие процессы в которых протекают иден­тично, но сдвинуты друг относительно друга на угловые интервалы в соответствии с принятым порядком работы двигателя. Момгнт, скручивающий коренные шейки, может быть определен как геомет­рическая сумма моментов, действующих на всех кривошипах, пред­шествующих данной шатунной шейке.

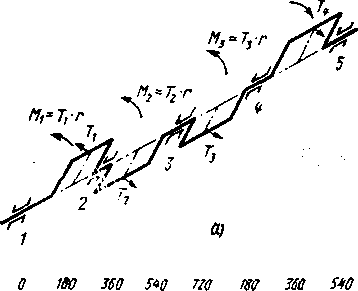
В качестве примера на рис. 1.13 представлена схема формирова­ния крутящих моментов в четырехтактном (г=4) четырехцилинд­ровом (г = 4) линейном двигателе с порядком работы цилиндров 1-3-4-2-1. При равномерном чередовании вспышек для данного дви­гателя угловой сдвиг между последовательными рабочими ходами составит 0 = 72071 = 72074—180°. Тогда с учетом порядка работы

Щядох работы цилимдроб J - 3 ~ 4 - 2 - )

	С?**		_V-s,			/S	z—
	/ч	9ншШ	0	V	ч/		0 л
					0
7S	9И‘18С					0 ^
§,,=	Ш' [\	А	Л	Л	Л	Л	Л
8*18(1* \ Г

в,-: =160'

8м = 720*

S-f

Ь)

Ряс. 1.13. Схема формиро­вания суммарного крутящего момента четырехтактного двигателя:

а — скеш моментов, действую­щих аа отдельных кривошипах; 6 — слеш построения суммарво- го крутящего момента

22

угловой сдвиг момента между первым и третьим цилиндрами со­ставит 180°, между первым и четвертым — 360°, а между лераым и вторым — 540°. Как следует из приведенной схемы, момент, скручивающий любую (r-ю) коренную шейку,

^М^^г I ^т‘-

0. 0

Кривая изменения по углу поворота кривошипа в этом слу­чае определяется суммированием кривых сил Т, действующих на всех I— 1 кривошипах, предшествующих ей.

Момент, скручивающий последнюю коренную шейку, является суммарным крутящим моментом двигателя М_г, который далее передается на трансмиссию. Совершаемая им работа может быть получена интегрированием M_z (<р) по углу поворота кривошипа <р в угловом интервале, соответствующем рабочему циклу двигателя в (в = 120° для четырехтактного двигателя и 6 = 360° для двухтакт­ного):

в

£i=f (<р) d(p, а

Нормирование ее на угловом интервале рабочего цикла дает средний суммарный крутящий момент

1 ^в

(<Р) ^d9>

⁹ о

соответствующий индикаторному моменту М_у развиваемому дви­гателем.

• Моменты, скручивающие шатунные шейки много- цилиндрового двигателя. В одноцилиндровом двигателе в ре­зультате действия суммарных сил на коренных шейках коленчатого вала возникают реакции Л, н Д_т, одна из которых, А, = 0,5Т, дейст­вующая в плоскости, перпендикулярной кривошипу, скручивает ша­тунную шейку. Тогда величина скручивающего момента будет рав­на М_шш = Л_тг=0,5Тг.

Представив миогоцилиндровый двигатель в виде совокупности одноцилиндровых и рассматривая только воздействие на кривоши­пы тангенциальных сил, получим момент, скручивающий г-ю ша­тунную шейку:

i⁼j^-!^-Rjт ⁼ Л/щ f-J-0,5Tj т,

где М_ш f — момент на i-й коренной шейке.

Момент Мцщ,) в функции угла поворота кривошипа называется «набегающим» на i-ю шатунную шейку.

23

1.2.7. ВЛИЯНИЕ КОНСТРУКТИВНЫХ СООТНОШЕНИЙ В КШМ НА ПАРАМЕТРЫ ДВИГАТЕЛЯ

Конструкция КШМ существенным образом влияет на харак­теристики ДВС, такие, как степень его форсированное™, габариты, масса, долговечность и т. д. Рассмотрим механизм влияния на параметры ДВС основных конструктивных соотношений в его КШМ: коэффициента Я = г//_Ш и отношения K=SjD.

• Отношение радиуса кривошипа г к длине шатуна 1щ (Я = г//_ш). Анализ влияния Я на параметры ДВС проведен при неизменном рабочем объеме и диаметре цилиндра D. В этом случае изменение Я вызывается вариациями длины шатуна. При уменьше­нии Я («длинный» шатун) возрастают масса т_ш и ее составляющие /Пща и т^. При этом произойдет увеличение инерционной силы К_т, что можно скомпенсировать противовесами на продолжении щек кривошипа. Влияние снижения Я на Pj противоречиво: с одной сто­роны, растет Шща и связанная с нею масса ntj, что должно привести к увеличению Pj. С другой стороны, из-за наличия X в выражении, оп­ределяющем величину амплитуды силы инерции второго порядка Pja, возможно ее уменьшение. Уменьшение X вызовет увеличение высоты и массы ДВС, что связано с «удлинением» шатуна. Более длинный шатун приводит также к уменьшению угла что вызы­вает уменьшение боковой силы N. Меньшие N и /? обеспечивают при прочих равных условиях снижение износа в подвижных сочленениях цилиндропоршневой группы.

У современных двигателей с искровым зажиганием (ДсИЗ) ша­туны, как правило, длиннее, чем у дизелей. Это связано с большей быстроходностью первых и превалирующим влиянием у них на Pj второй гармоники. В дизелях из-за более высоких максимальных газовых нагрузок поперечное сечение стержня шатуна больше и уве­личение /Под при удлинении шатуна оказывает на Р_} большее влия­ние, чем уменьшение амплитуды P_ja.

Износ цилиндра неравномерен — больше изнашивается та его сторона, к которой прижимается поршень при рабочем ходе, что связано с ростом Р_г и связанной с ней силой N, достигающих максимального значения вблизи ВМТ в начале такта расширения. При введении дезаксажа максимальный угол отклонения шатуна 0 при рабочем ходе по абсолютному значению становится меньше, чем наибольшее отклонение при такте сжатия, что позволяет вырав­нять износ цилиндра по его периметру.

Необходимо отметить, что применение «коротких» шатунов в некоторых случаях может усложнять компоновку двигателя, так как из-за больших значений ft... возможно задевание шатуна за нижнюю часть цилиндра или юбку поршня.

• Отношение хода поршня S к диаметру цилиндра D (K—S/D). При неизменном рабочем объеме двигателя V_k увели-

24

чмть К можно уменьшением D при одновременном увеличении хода поршня S (длинноходные двигатели). Уменьшить К можно путем сокращения S (короткоходные ДВС) и увеличения D. Выбор оп­тимальной для данной конструкции двигателя величины К в значи­тельной мере связан с получаемой при этом средней скоростью поршня c_a = Snj30. Данный параметр характеризует конструкцию ДВС с точки зрения ее динамической и тепловой напряженности, а также износа элементов двигателя (особенно его цилиндропорш­невой группы), Известно, что напряжения от инерционных нагрузок на элементы КШМ пропорциональны с а тепловая напряженность двигателя и линейный износ деталей цилиндросоршневой группы пропорциональны с_а.

Формальный анализ выражения, определяющего среднюю ско­рость поршня, показывает, что при неизменной частоте вращения коленчатого вала (и) можно ее снизить и, следовательно, улучшить рассмотренные характеристики двигателя за счет уменьшения S.

Однако при этом необходимо считаться с ростом инерционных нагрузок на элементы КШМ. Это объясняется тем, что масса дета­лей КШМ пропорциональна D³, в то время как снижение скорости поршня вследствие уменьшения его хода пропорционально D¹. При увеличении D растет площадь поршня и, следовательно, возрастают газовые нагрузки на КШМ.

Таким образом, уменьшение К неоднозначно влияет на долгове­чность двигателя. С одной стороны, она увеличивается из-за умень­шения с₀, а с другой — уменьшается из-за возрастания инерцион­ных и газовых нагрузок на детали КШМ. Какой из приведенных факторов окажет большее шншше, решают индивидуально для каждого конкретного случая.

В современных быстроходных ДсИЗ наблюдается тенденция к использованию короткоходных конструкций с К= 0,9...1,0, что поз­воляет получить дополнительный резерв увеличения К при неизмен­ной с,,. В дизелях с их меньшей быстроходностью используют более длинноходные КШМ с 1,0...1,2.

Уменьшение К приводит к увеличению габаритной длины ДВС и длины коленчатого вала. При этом также уменьшается высота камеры сгорания, что усложняет получение требуемой ее формы. Это может приводить к ухудшению условий протекания процессов смесеобразования и сгорания. У ДсИЗ возрастает также вероят­ность возникновения детонации. К положительным качествам ко- роткоходных конструкций следует отнести снижение теплоотдачи в стенки цилиндра, улучшение возможности увеличения проходных сечений горловин клапанов, обеспечение большего перекрытия шеек коленчатого вала, уменьшение поперечного сечения картера и мас­сы ДВС.

25

13. УДАРЫ В КРИВОШИПНО-ШАТУННОМ МЕХАНИЗМЕ

На протяжении рабочего цикла силы, действующие во всех соп- ряжениях кривошипно-шатунного механизма, многократно меняют свой знак. Изменение направления действия силы приводит к соуда- рению относительно перемещающихся звеньев и появлению вибра- ционных импульсов. Удары могут возникать в коренных и шатун- ных подшипниках коленчатого вала, в сопряжении шатун—поршне- вой палец—поршень, а также между поршнем и гильзой цилиндра.

В литературе, посвященной проблеме снижения шума двигателя, особенно большое внимание уделяется «перекладке» поршня под действием боковой силы N, как одной из наиболее вероятных причин повышенного шума двигателя:

ЛГ~ (Р_г+Pj) X sin (p.

Изменение знака этой силы указывает на возможность бокового перемещения поршня и удара о стенку цилиндра. В четырехтактном двигателе момент изменения знака боковой силы и количество перекладок определяются силами инерции Р_} и кривой sin <р. Исклю- чение составляет работа в ВМТ, где решающее значение имеет величина

газовых сил.

В современных автотрак- торных двигателях в зависимо- сти от конструктивных особен- ностей может наблюдаться различное изменение сил, дей- ствующих на поршень в об- ласти ВМТ

• На рис. 1.14 приведены кри- вые, показывающие изменение сил, действующих на поршень, для двух режимов работы дви- гателя. Первый из них соответ- ствует максимальному крутя- щему моменту, второй — но- минальной мощности. На пер- вом режиме газовые силы усу- губляют ударное воздействие поршня на стенку цилиндра, на втором — перекладка поршня от них отсутствует. Первый ре- жим характерен также для ди- зелей с малой и средней часто- той вращения (до 1500 мин^-1). При форсировании дизеля до 2500...3500 мин^-1 из-за значи- тельного роста сил инерции

Рис. 1.14. Силы, действующие на по­ршень, на режимах максимального крутя­щего момента (а) и максимальной мощ­ности (б)

26

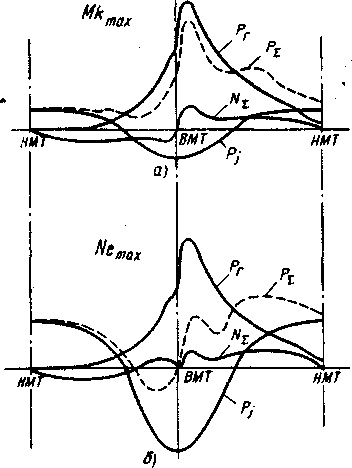
суммарная сила на участке перед ВМТ может стать отрицательной, что ослабит интенсивность перекладки в этой стадии цикла.

Для ДсИЗ характерно другое изменение сил, изображенных на рис. 1.14, б. Здесь следует иметь в виду также то, что эти двигатели имеют количественное регулирование. Удары поршня о стенку ци- линдра в двигателе с искровым зажиганием могут возникать в об­ласти ВМТ лишь при нагрузках более 75% от полной при частоте вращения вала не менее 2000...2500 мин'¹.

Во все остальные моменты рабочего цихла, когда происходит изменение знака боковой силы, возникает удар, интенсивность ко­торого растет с увеличением частоты вращения. При этом интенсив­ность удара помимо скоростного режима определяется величиной зазора в сопряжении поршень—гильза, массой деталей, соверша­ющих возвратно-поступательное движение, произведением хода по­ршня на диаметр. Увеличение всех перечисленных параметров при­водит к более интенсивному удару.

Движение, которое совершает поршень в двигателе под действи­ем боковой силы, является сложным. Обычно оно рассматривается как сумма поступательного движения центра тяжести поршневого комплекта и вращательного движения вокруг оси, проходящей че­рез центр масс и параллельной оси поршневого пальца.

Это движение поршня в пределах зазоров исследуется с помо­щью системы уравнений, описывающих плоскопараллельное движе­ние твердого тела. Особенно простой система получается в случае выбора осей координат, перпендикулярных оси пальца, одна из которых параллельна оси цилиндра.

На основании анализа такой системы уравнений В. Д. Курнатов вывел следующее выражение, характеризующее энергию, затрачен­ную на возбуждение колебаний при ударе поршня:

dN (0)

где значение производной от боковой силы при прохожде-

d <р

нии ее через нуль; т — масса деталей поршневого комплекта; А — диаметральный зазор между поршнем и цилиндром; р — радиус инерции поршневого комплекта; I — расстояние от оси вращения поршня до нижнего края юбки; С — расстояние между осью по­ршневого пальца и осью, проходящей через центр масс поршневого комплекта; А — числовой коэффициент; п — частота вращения.

Из этого выражения следует, что для снижения шума от ударов поршня более целесообразны конструкции с удлиненной юбкой, до (1,0.. .1,25) D. Дальнейшее увеличение длины юбки нецелесообразно из-за увеличения массы и радиуса инерции.

Смещение оси пальца относительно оси цилиндра может влиять

27

на скорость удара. Существует оптимальное значение такого сме- щения, лежащее в пределах до 0,03 D в сторону, противоположную вращению вала. Большие смещения оси пальца приводят к появле- нию момента от газовых сил, который усиливает удар. Смещение коленчатого вала относительно оси цилиндра также влияет на интенсивность перекладки.

В подшипниковых узлах КШМ изменение знака результиру- ющей силы не всегда приводит к удару сопрягающих звеньев. Перемещение элементов подшипника друг относительно друга мо-

жет происходить с контактом или без контакта между ними (сво- бодное движение). Переходный процесс от свободного движения к движению с контактом сопрово- ждается соударением.

В случае потери контакта меж- ду деталями соединения интенси- вность удара зависит как от вели- чины зазора, так и от скорости нарастания нагрузки в момент со- ударения. При сохранении конта- кта интенсивность ударных явле- ний определяется только характе- ром приложенной нагрузки.

Условия возникновения соуда- рений и характер приложения ударных нагрузок в шатунных подшипниках могут быть рассмо- трены аналитически. Данная за- дача сводится к изучению реакции в подшипнике.

На рис. 1.15 приведены схемы механизма, учитывающие нали- чие зазора в шатунном подшип- нике, и кривая динамической ре- акции R. Уравнения динамичес-

кой реакции Л и ее линии действия, задаваемой углом у, находят, проецируя все силы на оси R и Q:

Рис. 1.15. Схема КШМ с учетом зазо­ра Л в шатунном подшипнике (а) в гра­фик зависимости динамической реак­ции R от угла поворота коленчатого вала (б); А — участок резкого нараста­ния нагрузки

где f{<p)

L V

R—fW) sin у + v (<р) cosy,

cosg>+Acos2p

--simp;

mjroy j J

v(qD) = (l+fc)X

x cos q> + X cos 2(p —; k=m_uajmj, — приведенная масса ниж-

mjra>²

ней головки шатуна; m_t — масса деталей, движущихся возвратно-

28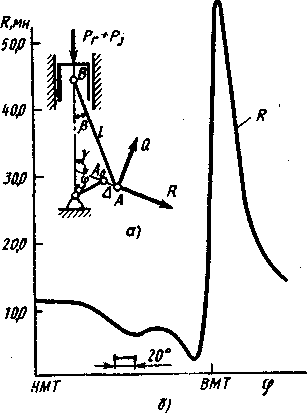

поступательно; а> — угловая скорость коленчатого вала; X — от- ношение радиуса кривошипа к длине шатуна. '?

Условие потери контакта между перемещающимися элементами подшипника таково: Л = 0. Теоретически это может быть выполнено при одновременном выполнении условий

9 = 2лМ*=1, 2,3,...);

Р_т= (1 + к+Л) т_}ш^г.

Согласно данным табл. 1.2, в двигателях с искровым зажигани- ем эти условия соблюдаются всегда, в дизелях — только при повы- шенных частотах вращения.

Если при анализе динамических реакций в коренных опорах двигателей принимать во внимание зазор, то приходится отказы- ваться от статической определенности. Такое допущение можно сделать применительно к трехопорным валам, и тогда условия обращения в нуль динамической реакции могут быть выражены аналитически подобно тому, как это было сделано для шатунных подшицников. Анализ более сложных схем можно провести, приняв некоторые упрощения. Налример, для каждого коренного подшип-

ника коленчатого вала ЗИЛ-130 можно составить выражение для _КЦ' определения результирующей to силы (рис. 1.16) от динамических усилий Kf, действующих на со- * ответствующих кривошипах, и силы инерции вращающихся масс Р_с кривошипа:

где I, j, т. п — порядковые но- _д мера соответственно шатунных подшипников правого (i=l_t 2, __г

3. 4) и левого (j—5, 6, 7, 8) рядов цилиндров, шатунных -*

(л = 1, 2, 3, 4) и коренных (т—\,

2. 3, 4, 5) шеек коленчатого вала -е двигателя.

Основное допущение состоит ~⁸ в следующем: действующие си- лы R{ k Р_а (в каждом кривоши- ⁴⁰ пе) воспринимаются лишь двумя

ближайшими подшипниками, a ^^HC- Силы, действующие на ко-

еилы ннрппии от ппатпякыгит™ Реняые подшипники колечатого вала

силы инерции от вращающихся зиЛ-130 («=1000 мин'¹,

противовесов второго И третье- 100%-ное открытие Дроссельной за-

ГО кривошипов — вторым и чет- слонки)

29

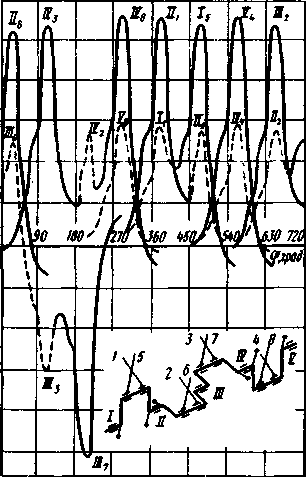
вертым коренными подшипниками. Из рис. 1.16 видно, что на динамическую реакцию в коренном подшипнике большее влияние оказывают силы, действующие в ближайших шатунных подшип­никах. На некоторых режимах (наиболее вероятных для третьего коренного подшипника) существуют условия, когда динамическая реакция равна нулю. Естественно, что при указанных допущениях величины Яу являются приближенными.

Данный анализ справедлив для работы КШМ без учета гидроди­намической силы, возникающей при вращении цапфы в подшипнике и наличии масла в зазоре между ними.

В условиях нормальной эксплуатации соударения в подшипни­ках недопустимы, и при проектировании подшипника стремятся создать такой гидродинамический режим работы, который исклю­чил бы уменьшение радиального зазора под действием рассмотрен­ных выше силовых факторов до величин, меньших h^, позволяю­щих сохранить условия жидкостного трения.

Таблица 1.2

Tton Д ВС	п, мии »	1+Л		Тип ДВС	я, МНВ'1	1+Л+Л	Реп
		Гш				пцпо1 Fa
	1300	0,45...1,35			2500	0,78...1,5
	1600	0,82.„1,78	3,9...	С искровым	2800	0,98.-1,88	0,9...
Дизель	1900	1.5...2	...4,6	зажиганием	3000	1,13-2,16	...1,4
	2100	1-2,5			3600	1,6-3,1
	4000	4...б			4000	2-2,45