Вопрос №52 Классификация алу. Выполнение операций сложения (вычитания) и умножения в алу. Классификация алу:
По способу представления чисел:
для чисел с фиксированной запятой (с целыми, дробными)
для чисел с плавающей запятой
для десятичных
По разрядности:
С постоянной
С переменной
По используемой системе счисления:
С использованием позиционных систем
С использованием непозиционных систем
По способу представления отрицательных чисел:
Обратный код
Дополнительный код
По способу действия над операндами:
Последовательный
Параллельный
Параллельно-последовательный
По структуре
С непосредственными связями
С магистральной структурой
По способу организации работы:
Синхронные
Асинхронные
По характеру использования элементов и узлов:
Блочные
Многофункциональные
По типу расширенных возможностей:
АЛУ с дополнительными регистрами
Многосумматорные АЛУ
Алгоритмы сложения (вычитания) и умножения в алу
Структурная схема микропрограммы сложения показана на рис. 2. Выполнение этого алгоритма состоит в следующем:
Первое слагаемое а устанавливается на Рг1, анализируется его знак: если знак отрицательный, то операнд инвертируется и передается на Рг3, если положительный - передается без инверсии через Рг2 на Рг3.
Второе слагаемое также устанавливается на Рг1 и анализируется его знак: если знак отрицательный, то операнд инвертируется, если положительный - сразу начинается суммирование операндов на Рг2 (сумматоре).
После суммирования анализируется знак результата: если результат отрицательный, то он инвертируется, если положительный - добавляется “+1” ЦП к младшему разряду результата и выполняется анализ признаков переполнения.
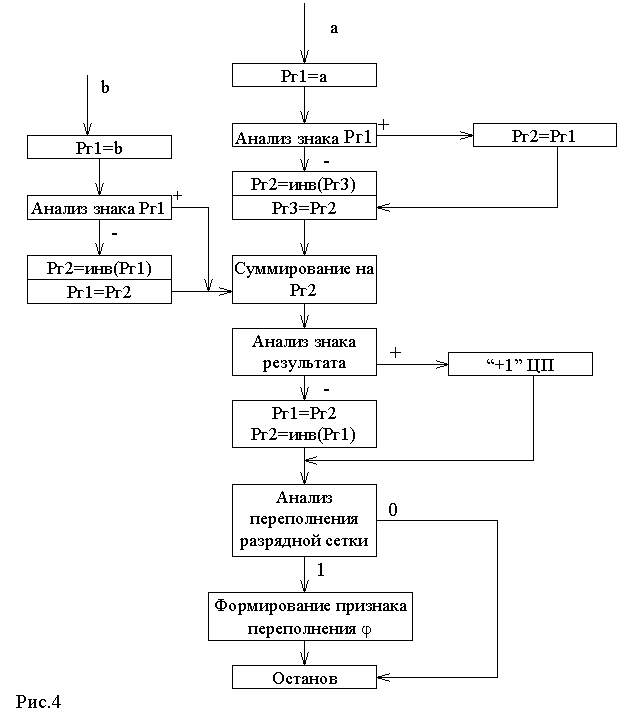
Рис.2
В случае переполнения разрядной сетки машины формируется признак переполнения , если переполнение отсутствует, то выполняется переход на конец микропрограммы сложения.
Для того чтобы структурная схема, показанная на рис. 2 могла выполнять операцию вычитания, достаточно перед выполнением операции проинвертировать знак второго слагаемого.
Операция алгебраического вычитания Z=X-Y=X+(-Y) может быть сведена к изменению знака вычитаемого Y и операции алгебраического сложения. Изменение знака - принятый в Рг1 код инверсно передается в РгА и при сложении осуществляется подсуммирование 1 в младший разряд сумматора.
Теперь рассмотрим алгоритм умножения. Умножение двоичных чисел с фиксированной запятой можно свести к последовательности сдвигов и сложений. Наиболее удобен следующий алгоритм: умножение начинается с младших разрядов множителя, который сдвигается вправо, сумма частичных произведений также сдвигается вправо, множимое – неподвижно. На рис. 3 показана графическая интерпретация этого алгоритма.
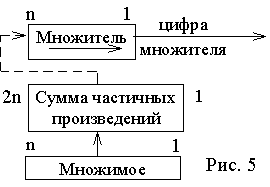
Рис. 3
Вначале операции все регистры устанавливаются в нулевое состояние.
Множимое и множитель располагаются в определенных регистрах, предусматриваются также регистры, в которых образуется сумма частичных произведений.
Анализируется младший разряд множителя: если он имеет значение “1”, то к сумме частичных произведений прибавляется множимое.
Производится сдвиг суммы частичных произведений и множителя на один разряд вправо.
Действия 3 и 4 повторяются n раз (n - разрядность сомножителей). Структурная схема микропрограммы умножения показана на рис. 4. Ввиду громоздкости деление здесь не рассматривается.
Рис. 4
Умножение, начиная с младших разрядов множителя со сдвигом суммы частичных произведений вправо и при неподвижном множимом.
1. Берутся модули от сомножителей.
2. Исходное значение суммы частичных произведений принимается равным 0
3. Если анализируемая цифра множителя равна 1, то к сумме частичных произведений прибавляется множимое; если эта цифра 0, прибавление не производится.
4. Производится сдвиг суммы частичных произведений вправо на один разряд.
5. Пункты 3 и 4 последовательно выполняются для всех цифровых разрядов множителя, начиная с младшего.
6. Произведению присваивается знак плюс, если знаки сомножителей одинаковы, минус - в противном случае.
Умножение, начиная с младших разрядов множителя при сдвиге множимого влево и неподвижной сумме частичных произведений
Регистр множителя должен иметь цепи сдвига вправо, регистр множимого - влево, сумматор не должен иметь цепей сдвига. Последовательность действий определяется младшим битом регистра множителя. При этом методе регистр множимого и сумматор частичных произведений должны иметь двойную длину. Этот метод требует больше оборудования, но никаких преимуществ не дает, поэтому его применение нецелесообразно.
Умножение, начиная со старших разрядов множителя при сдвиге суммы частичных произведений влево и неподвижном множимом
Регистр множителя и сумматор частичных произведений должны иметь цепи сдвига влево. Регистр множимого не имеет цепей сдвига. Последовательность действий в каждом цикле выполнения умножения определяется старшим разрядом регистра множителя. При этом методе сумматор частичных произведений должен иметь двойную длину. И данный метод требует дополнительного по сравнению с первым методом оборудования. Но он применяется в некоторых АЛУ, т.к. позволяет без дополнительных цепей сдвига выполнять и деление (а при первом методе для выполнения деления необходимы дополнительные цепи сдвига влево в регистре множимого (частного) и в сумматоре частичных произведений (разностей).
Умножение, начиная со старших разрядов множителя при сдвиге вправо множимого и неподвижной сумме частичных произведений
Регистр множителя должен иметь цепи сдвига влево, регистр множимого - цепи сдвига вправо. Сумматор частичных произведений не имеет цепей сдвига. Последовательность действий на каждом шаге определяется старшим разрядом регистра множителя. При этом методе и регистр множимого, и сумматор частичных произведений должны иметь двойную длину. Однако, как и третий метод, он не требует дополнительных цепей сдвига для выполнения деления. Также в случае этого метода можно совмещать во времени операции сдвига и сложения и за этот счет увеличить быстродействие АЛУ при выполнении умножения (а также деления).
Если необходимо образование произведения двойной длины (напр. при операциях с целыми числами), то наиболее экономичным является первый способ (т.к. все регистры одинарной длины). Если в результате умножения достаточно иметь произведение одинарной длины, то целесообразно использовать либо 1ый, либо 4ый метод умножения. При использовании 1го требуется введение дополнительных цепей сдвига для реализации деления, а при использовании 4го необходимо удлинение сумматора. При образовании произведений одинарной длины простое отбрасывание младших разрядов вносит погрешность, которая будет накапливаться, т.к. произведение всегда будет вычисляться с недостатком. Поэтому для повышения точности вычислений часто производят округление результата умножения, вследствие чего погрешность становится знакопеременной. Для округления длина сумматора увеличивается на 1 разряд. После образования произведения к этому дополнительному разряду добавляется 1. Если он был равен 0, то произведение получается с недостатком. Если был равен 1, то произведение получается с избытком. При этом максимальное значение погрешности равно половине 1 младшего разряда.