9.3. Минимизация прогноза рассогласования [15]
В частном случае при отсутствии ограничений на управления (302) задача минимизации прогноза рассогласования может быть решена в явном виде. Максимальная точность регулирования достигается, если управления изменяются на каждом шаге так, чтобы обеспечить нулевое значение прогноза рассогласования:
. (305)
Подставляя в (305) выражения (303), (304) и разрешая полученное матричное уравнение, получаем выражения для оптимального управления при отсутствии ограничений:
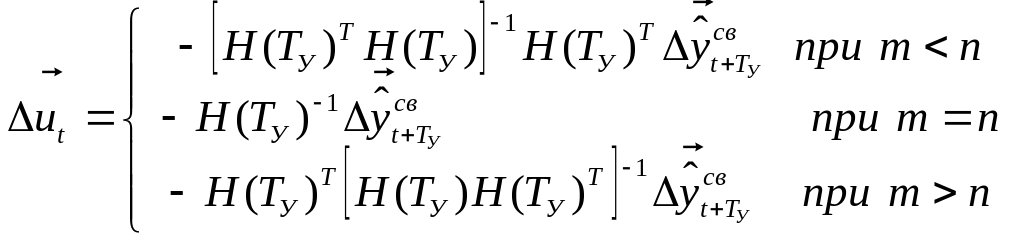
Решения
при
(число управлений не равно числу
регулируемых переменных) получены с
использованием понятия обобщенной
обратной матрицы и обладают минимальной
нормой.
При наличии ограничений (302) решения уравнения (305) в общем случае не существует (физически это означает, что при наложенных ограничениях нельзя добиться точной компенсации прогноза рассогласования). Поэтому от задачи компенсации прогноза рассогласования в общем случае следует перейти к задаче его минимизации:
. (306)
К сожалению, задача (306) с ограничениями (302) допускает только алгоритмическое решение. Одной из возможных постановок является решение задачи (306) как задачи с квадратичным критерием качества:
, (307)
где
и
–
соответственно (
)
– и (
)
– диагональные весовые матрицы.
Первое слагаемое вводится в критерий задачи (307) для минимизации прогноза рассогласования, а второе – для минимизации изменения вектора управления.
Подставляя в (307) выражения (303), (304) и вводя обозначения:
,
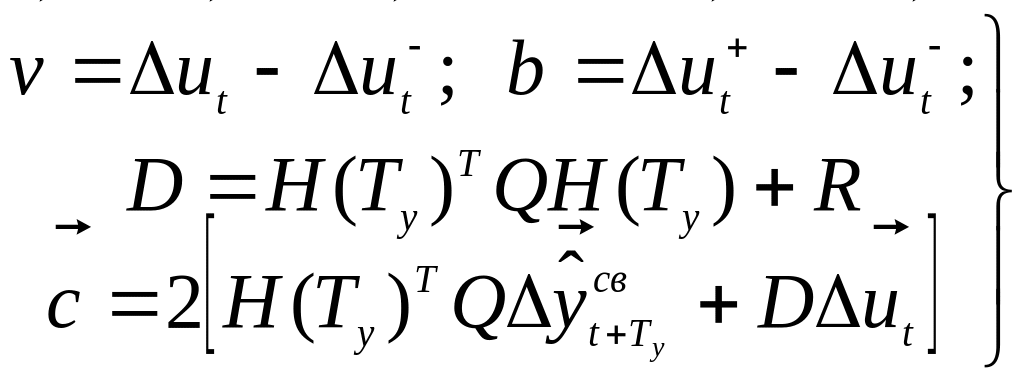можно преобразовать задачу (307) с ограничениями (302) к виду:
(308)
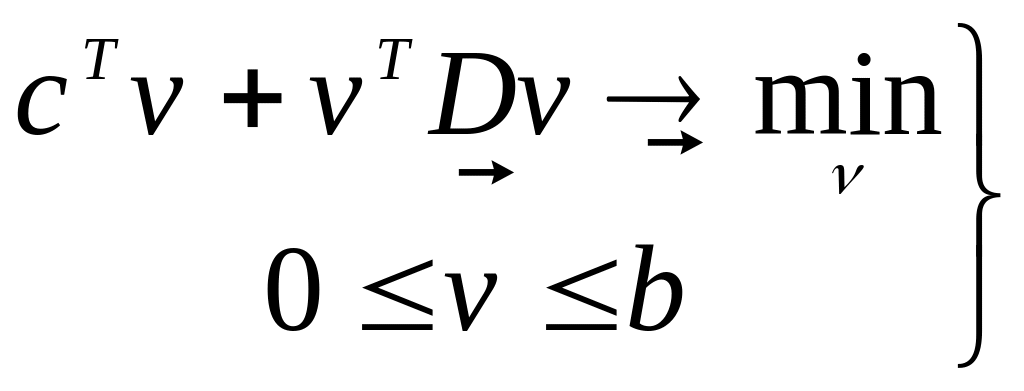
Задача (308) есть частный случай задачи квадратичного программирования, в которой требуется отыскать экстремум квадратичной целевой функции многих переменных при линейных ограничениях-неравенствах и условиях неотрицательности переменных:
(309)
,
где 
- n-вектор
переменных задачи;
-
n-вектор
коэффициентов линейных членов целевой
функции Z;
D – (n×n) – симметрическая матрица коэффициентов квадратичных членов целевой функции;
А – (m×n) – матрица коэффициентов ограничений-неравенств;
-
m-вектор
свободных членов ограничений.
9.4. Сведение задачи квадратичного программирования к задаче о линейной дополнительности [17, 14]
Одним из широко распространённых в настоящее время способов решения задачи квадратичного программирования является сведение этой задачи к задаче о линейной дополнительности.
Задачей
о линейной дополнительности называется
задача об отыскании векторов
и
таких, что выполняются условия:
(310.а)
(310.б)
(310.в)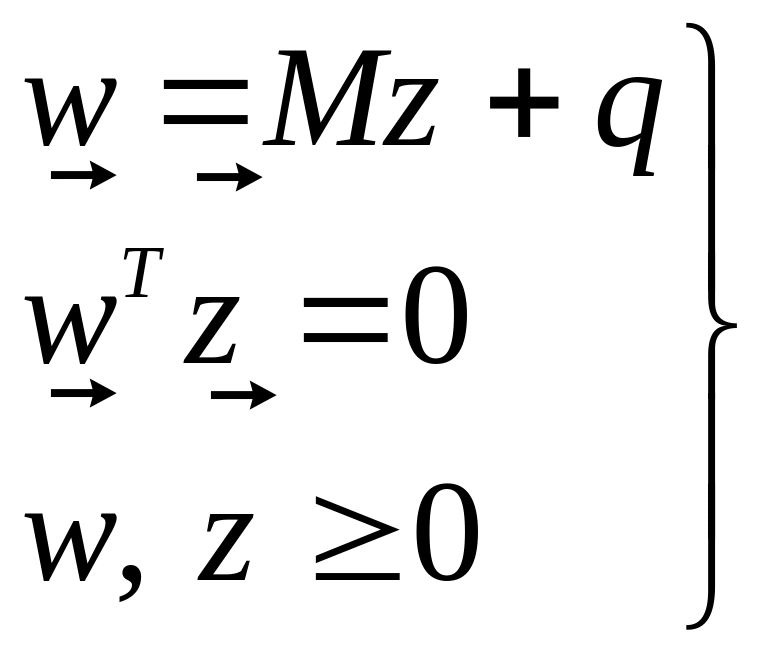
.
Условия
(310.а) есть ограничения-равенства. Входящие
в них p-векторы
называются соответственно векторами
базисных, свободных переменных и
свободных членов ограничений.
M – (p×p) – квадратная матрица коэффициентов ограничений.
Свободные переменные всегда равны нулю. Базисные переменные положительны. Значения базисных переменных при равенстве нулю свободных называют базисным решением системы (310.а).
Условие
(310.б) называют условием дополняющей
нежёсткости. Согласно этому условию
произведение любой пары переменных
и
должно быть равно нулю, для чего одна
из этих переменных всегда должна быть
равна нулю, а вторая больше нуля. Поэтому,
если не равная нулю переменная
входит в число базисных, то равная нулю
переменная
должна быть свободной и наоборот.
Переменные wi
,
zi
называются парой взаимодополняющих
(дополнительных) переменных.
Условия (310.в) называются условиями неотрицательности переменных.
Для того чтобы свести задачу квадратичного программирования (309) к задаче о линейной дополнительности (310), запишем необходимые условия экстремума (условия Куна-Таккера) для задачи (309):
(311)
,
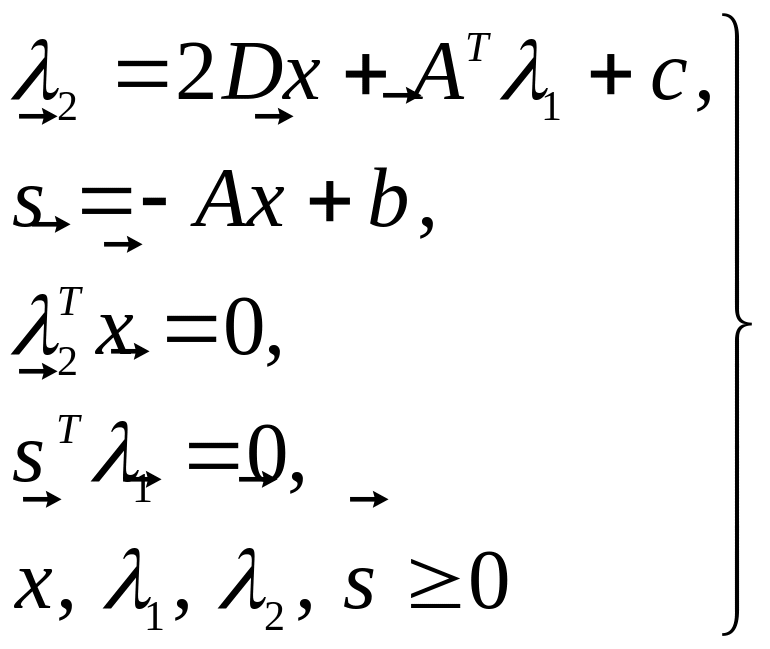где 
- соответственно m-
и n-
векторы неопределённых множителей
Лагранжа для ограничений-неравенств и
условий неотрицательности переменных
в задаче квадратичного программирования,
-
m-вектор
дополнительных неотрицательных
переменных, вводимых в ограничения-неравенства
для преобразования их в равенства.
Вводя обозначения
;
;
;
,
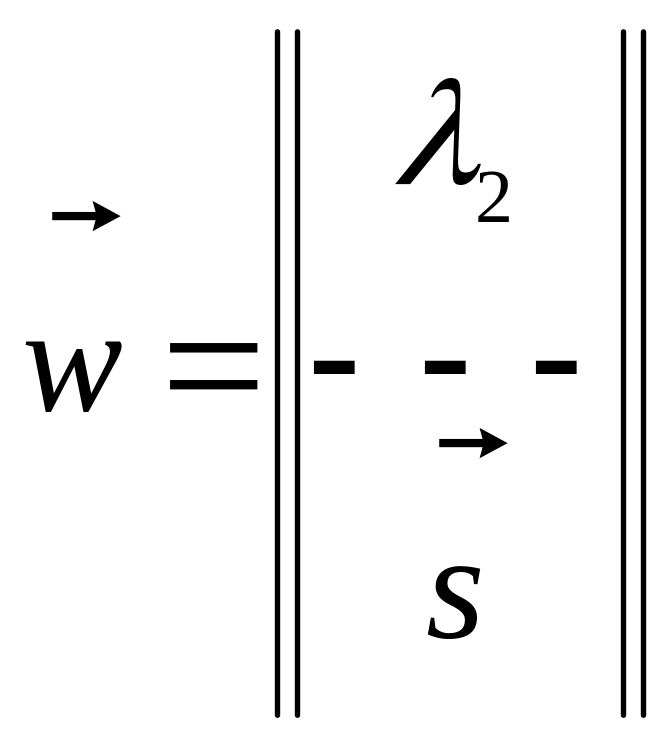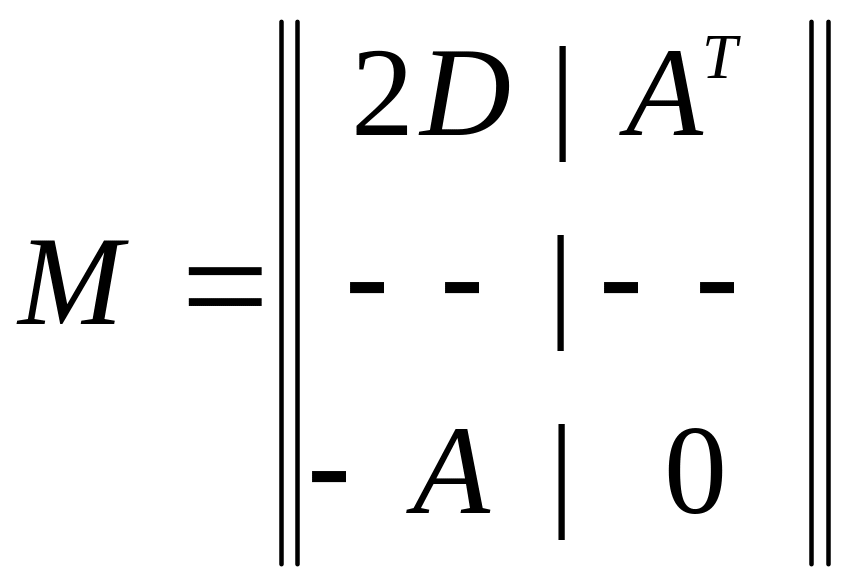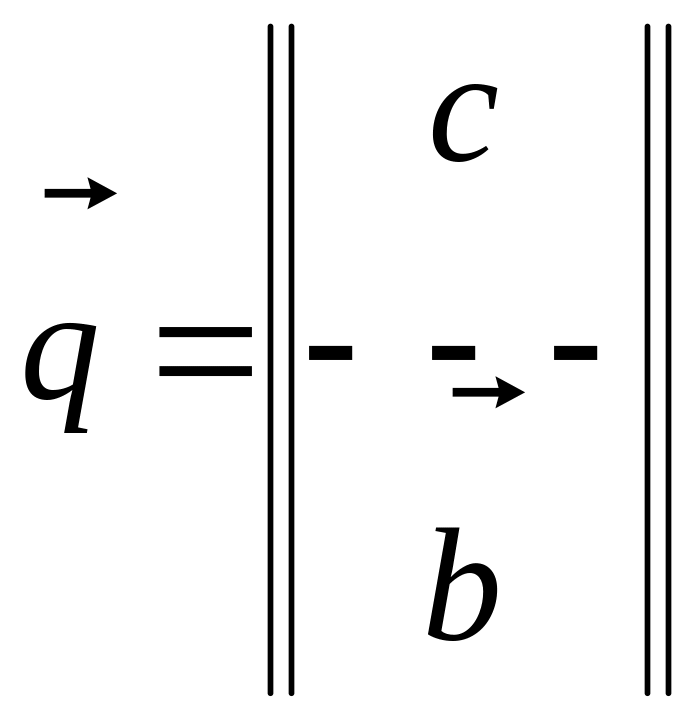можем записать (311) в форме (310) и тем самым свести задачу квадратичного программирования к задаче о линейной дополнительности.