Модификации цифровых регуляторов

Они определяются, в основном, способами численного интегрирования и дифференцирования, используемыми для реализации И- и Д- составляющих закона регулирования. Например, выше приведены выражения (189) для коэффициентов передаточной функции (188) ПИД-регулятора, полученные при использовании для реализации И-составляющей модифицированного метода прямоугольников. Если же для реализации И-составляющей использовать метод трапеций, выражения для коэффициентов b₂, b₁ трансформируются следующим образом:

Формулы численного дифференцирования обычно получают дифференцированием интерполяционных формул, используемых для описания временных последовательностей. Наиболее распространенными являются интерполяционные формулы Лагранжа и Ньютона. Например, при использовании интерполяционной формулы Лагранжа для полинома второго порядка, построенной по трем узлам интерполяции, можно получить следующее уравнение дифференциатора [6, 7]:

которому соответствует следующая передаточная функция:

(сравните с передаточной функцией (180)).

6.5. Расчет настроек цифровых регуляторов

Упрощенные формулы для расчета настроек цифровых регуляторов

Предполагается, что объект регулирования представлен моделью инерционного звена первого порядка с чистым запаздыванием (8) с параметрами K_об, T_об, _об.

В качестве примера приведем упрощенные формулы для определения параметров настройки одной из модификаций цифрового ПИД-регулятора, описываемого уравнением [5]:

Цифровые системы регулирования с конечной длительностью

переходных процессов (Системы с апериодическими регуляторами)

Специфической особенностью цифровых систем регулирования является то, что при определенных условиях переходной процесс заканчивается в них за конечное минимальное время и носит при этом апериодический характер. Регуляторы, обеспечивающие такой переходной процесс, называются регуляторами конечной длительности или апериодическими регуляторами (А-регуляторами). Ниже рассматривается расчет систем, переходной процесс в которых длится число периодов квантования k равное порядку передаточной функции замкнутой системы:

t_p=kT

(t_p – время переходного процесса)

Рассмотрим передаточную функцию замкнутой системы:

(193)

Характеристическое уравнение замкнутой системы

(194)

содержит k корней z_i и по формуле Виета может быть представлено в виде:

(195)

Предположим, что все корни равны нулю:

тогда (195) принимает вид:

(196)

Сравнивая (196) и (194) убеждаемся, что для перехода от (195) к (196) необходимо все коэффициенты a_i, кроме a_k, приравнять нулю:

При этом передаточная функция (193) преобразуется к так называемой желаемой передаточной функции замкнутой системы:

(197)

где

.

Пусть, например, Взяв обратное Z-преобразование от передаточной функции (197), получаем следующее выражение для нахождения выходной величины:

(198)

Строим по выражению (198) переходной процесс

Таким образом, начиная с n=k=5, переходная характеристика принимает постоянное значение, следовательно, переходной процесс заканчивается за пять интервалов квантования.

В общем случае переходной процесс при нулевых корнях характеристического уровня замкнутой системы (195) заканчивается за k периодов квантования (k – порядок характеристического уравнения). Такие системы и называются системами с конечной длительностью переходного процесса. При этом оказывается, что переходной процесс в системе конечной длительности является в то же время минимальным по длительности по сравнению с любыми другими значениями корней z_i и апериодическим.

Запишем теперь условия конечной длительности переходного процесса. Как отмечалось, для получения такого процесса все коэффициенты характеристического уравнения (194), кроме a_K, должны быть равны нулю:

(199)

Разрешая систему уравнений (199) относительно настроечных параметров регулятора, получаем значения искомых параметров.

В качестве А-регулятора используется регулятор с дробно-рациональной передаточной функцией. Для того, чтобы число уравнений для определения параметров настройки регулятора было не меньше числа параметров регулятора, порядок передаточной функции А-регулятора должен быть равен порядку приведенной непрерывной части. Если, кроме того, мы хотим иметь астатический регулятор, обеспечивающий нулевую статическую ошибку в замкнутой системе, знаменатель передаточной функции регулятора должен содержать сомножитель (z-1) (как и все астатические регуляторы: И-, ПИ-, ПИД)

Отметим, что цифровая АСР с А-регулятором имеет конечный, апериодический и оптимальный по длительности переходной процесс только при ступенчатом воздействии.

К недостаткам систем с А-регуляторами можно отнести следующие:

1. Передаточная функция А-регулятора зависит от передаточной функции приведенной непрерывной части и усложняется с ростом порядка последней.

2. С уменьшением периода квантования возрастают максимальное значение регулирующего воздействия и значения параметров настройки регулятора.

В качестве примера рассмотрим цифровую АСР с объектом регулирования в виде инерционного звена первого порядка и ПИ-регулятором.

Напомним (см. раздел 6.3), что передаточная функция приведенной непрерывной части, соответствующая данному объекту, равна

(200)

где

– параметры инерционного звена первого порядка.

Тогда с учетом передаточной функции ПИ-регулятора (176) пердаточная функция замкнутой системы равна:

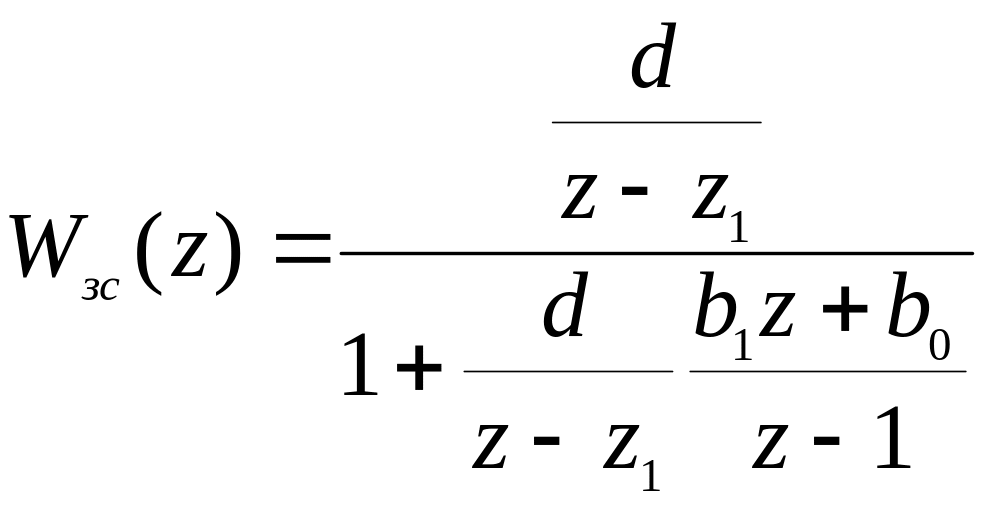
Характеристическое уравнение замкнутой системы:

Условия конечной длительности переходного процесса (199):

,

или с учетом обозначений для и :

.

Решая последнюю систему уравнений, получаем настройки ПИ-регулятора, обеспечивающие конечную длительность переходного процесса:

При .

Желаемая передаточная функция замкнутой системы (197):

,

т.е. переходной процесс в рассматриваемой системе действительно заканчивается за .

Расчет настроек цифровых регуляторов методом расширенных частотных характеристик

Нахождение расширенных частотных характеристик

Для нахождения расширенных частотных характеристик следует в выражение для передаточной функции подставить

.

Обозначив для упрощения записи

,

получаем

. (201)

Приведем в качестве примеров выражения для расширенных частотных характеристик приведенной непрерывной части (200) и ПИ-регулятора (176).

РЧХ приведенной непрерывной части (200):

РЧХ ПИ-регулятора (176):

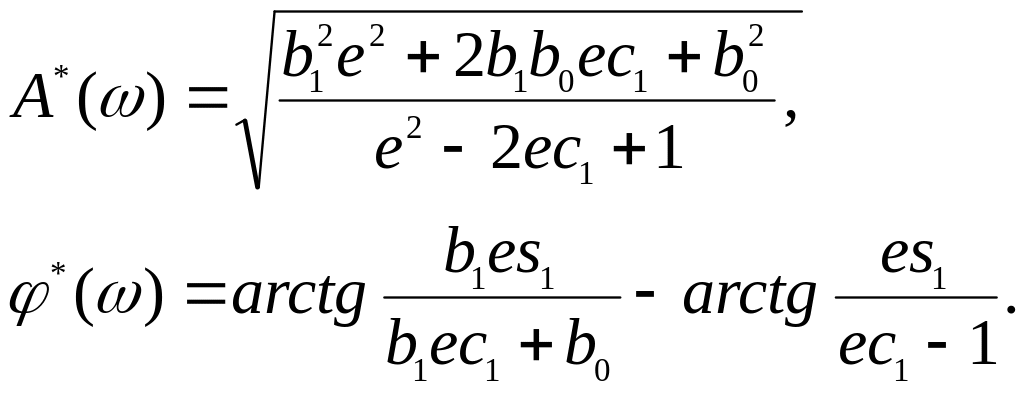
Нахождение ЛРЗ

Для нахождения уравнения линии равного затухания используются дискретные аналоги условий заданной колебательности переходного процесса в замкнутой системе (36):

(202)

Поступая так же, как при выводе уравнений ЛРЗ для непрерывных систем, можно получить дискретные аналоги этих уравнений.

Дискретный аналог выражений (41) для П-регулятора:

(203)

Дискретный аналог выражений (43) для И-регулятора:

(204)

Дискретный аналог уравнений (47), (50) ЛРЗ для ПИ-регулятора:

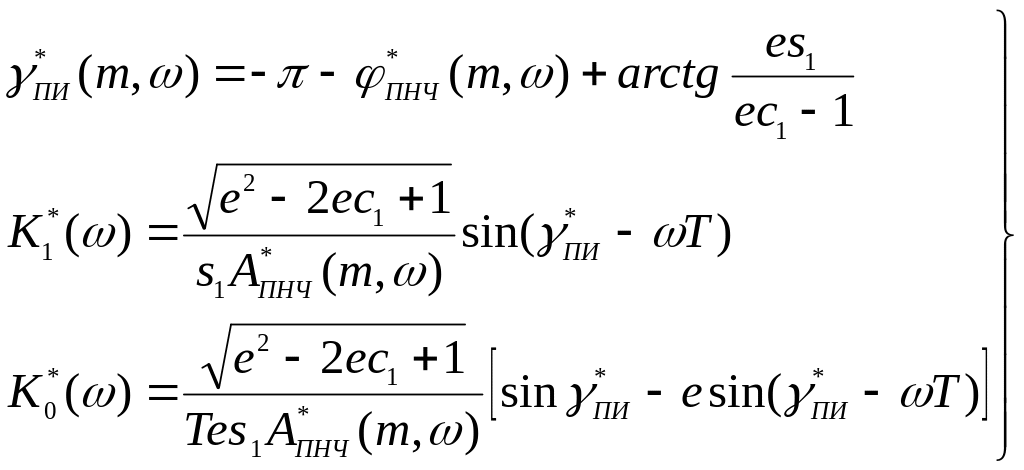(205)

Дискретный аналог уравнений (59) для ПИД-регулятора:

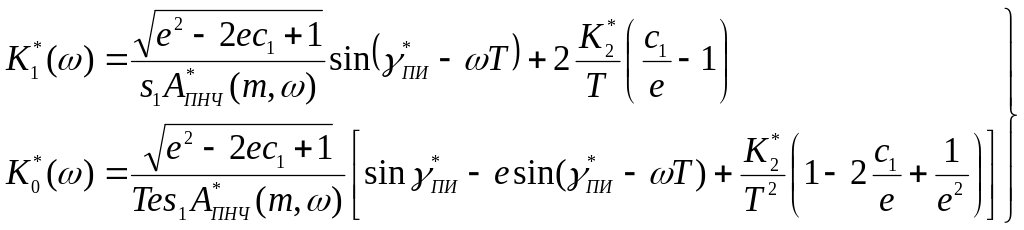(206)

Особые прямые

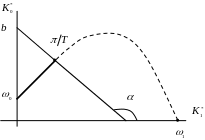Специфической особенностью ЛРЗ для дискретных систем является то, что при ЛРЗ вырождается в особую прямую (рис. 74)

Рис. 74.

Запишем уравнение особой прямой для ЛРЗ для системы с ПИД-регулятором.

При

и уравнения (206) вырождаются в особую прямую с уравнением:

(207)

(На рис. 74 ).

Следует заметить, что если , т.е. период квантования достаточно мал и выбран правильно, частота оказывается за пределами частотного диапазона, в котором строится ЛРЗ, поэтому наличие особой прямой не сказывается на форме ЛРЗ. Если же период квантования слишком велик и выбран неправильно, т.е. , ЛРЗ вырождается в особую прямую.