6.2. Структурная схема цифровой системы регулирования (рис. 61)
Рис. 61.
На рис. 61 обозначено:
Wоб(p) – передаточная функция объекта регулирования. Объекты регулирования, как правило, являются непрерывными звеньями, на входе и выходе которых действуют непрерывные во времени сигналы,
– идеальный
амплитудно-импульсный модулятор
(импульсный элемент),
Wрег(z) – передаточная функция дискретного регулятора,
Wф(p) – передаточная функция фиксирующего элемента (экстраполятора), служащего для преобразования выходной последовательности импульсов регулятора в непрерывный сигнал на входе объекта. Чаще всего используются простейшие экстраполяторы, запоминающие мгновенные значения выходного сигнала дискретного регулятора на весь период квантования, в результате чего последовательность импульсов преобразуется в непрерывную ступенчатую функцию. Такие экстраполяторы называются экстраполяторами нулевого порядка (ступенчатыми экстраполяторами).
Реакция экстраполятора нулевого порядка на мгновенный импульс представляет прямоугольный импульс длительностью T (рис. 62) и по определению является весовой функцией фиксатора, которую можно представить в виде двух смещенных ступенчатых функций:
wф(t)=1[t] – 1[t – T] (152)
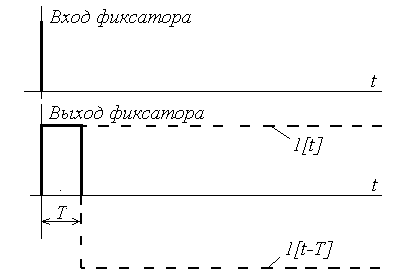
Рис. 62.
Из теории управления известно, что передаточная функция звена есть преобразование Лапласа его весовой функции, следовательно, передаточную функцию фиксатора можно найти, определив преобразование Лапласа весовой функции (152):
(153)
В исходной структурной схеме цифровой системы на рис. 61 действуют как непрерывные (на входе и выходе объекта регулирования), так и дискретные (на входе и выходе регулятора) сигналы. Т.е. исходная схема является дискретно-непрерывной. Это создает неудобства при ее анализе. Поэтому исходную структурную схему преобразуют к эквивалентной непрерывной или эквивалентной дискретной. Поскольку преобразование дискретно-непрерывной системы к эквивалентной непрерывной возможно только при малых значениях периода квантования, рассмотрим преобразование дискретно-непрерывной системы к эквивалентной дискретной. С этой целью вводится понятие приведенной непрерывной части (ПНЧ), к которой относят объект регулирования и экстраполятор:
WПНЧ(p)=Wф(p)Wоб(p) (154)
Введение ПНЧ позволяет перейти от непрерывного сигнала на входе объекта регулирования к дискретному сигналу на входе ПНЧ. Считая условно выходной сигнал ПНЧ или, что то же, объекта регулирования также дискретным, можем преобразовать исходную структурную схему цифровой системы к виду (рис. 63)
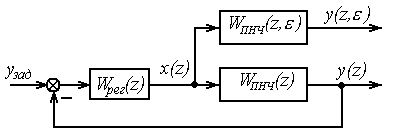
Рис. 63.
В этой структурной схеме действуют только дискретные сигналы. Таким образом, структурная схема цифровой АСР отличается от структурной схемы непрерывной АСР тем, что вместо непрерывных передаточных функций используются дискретные передаточные функции и вместо объекта регулирования используется ПНЧ.
Если нас интересует поведение регулируемой переменной внутри периода квантования, в структурную схему следует дополнительно ввести передаточную функцию ПНЧ для смещенной регулируемой величины WПНЧ(z,). Для ее нахождения используется Z-преобразование смещенной решетчатой функции на выходе ПНЧ Y(z,).