Временные характеристики

Переходной характеристикой цифровой системы регулирования называется реакция на единичную ступенчатую решетчатую функцию, определяемую следующим образом:

.

Z-изображение единичной ступенчатой функции:

. (149)

Дискретная весовая функция w[nT] определяется так же, как и непрерывная – реакция на мгновенный импульс единичной площади.

Частотные характеристики дискретных систем

Так же, как и в случае непрерывных систем, частотные характеристики находятся заменой p на j, или с учетом (141) z на e^iT. Выражение Y^*(j), получаемое при замене z=e^iT в Z-изображении Y(z) решетчатой функции называется спектром Фурье или изображением по Фурье решетчатой функции. Отношение спектров Фурье выходного и входного сигналов называется частотной передаточной функцией (комплексной частотной характеристикой) дискретной системы:

.

АФХ, АЧХ и ФЧХ дискретных систем определяются так же, как и для непрерывных. Годограф частотной передаточной функции называется АФХ цифровой системы. Зависимости модуля и фазы частотной передаточной функции от частоты определяют соответственно АЧХ и ФЧХ цифровой системы.

Спектры решетчатых функций и частотные характеристики цифровых систем так же, как Z-изображения решетчатых функций и передаточных функций дискретных систем, обладают свойством периодичности по частоте, поскольку функция

Периодична с периодом .

Кроме периодичности, частотные характеристики дискретных систем обладают еще одним свойством: они симметричны в диапазонах частот и . Другими словами, интервал не содержит новой информации о частотных характеристиках по сравнению с интервалом . При этом на концах этого интервала частотная передаточная функция принимает вещественные значения, поскольку при =0 e^jT=1 и при =_k/2 e^jT= –1.

Таким образом, частотные характеристики цифровых систем можно изображать в частотном диапазоне от 0 до _k/2 (или от 0 до _k), причем на концах этих интервалов АФХ принимает вещественные значения.

Итак, в то время как частотные характеристики непрерывных систем изображаются на интервале , частотные характеристики цифровых систем достаточно изображать на интервале .

В силу периодичности частотных характеристик спектр решетчатой функции с точностью до 1/T представляет бесконечную сумму спектров исходного непрерывного сигнала, сдвинутых на k_k (k – любое целое число):

Поэтому спектры непрерывной и решетчатой функций (а, следовательно, и частотные характеристики непрерывной и дискретной систем) совпадают только в области малых частот (рис. 59)

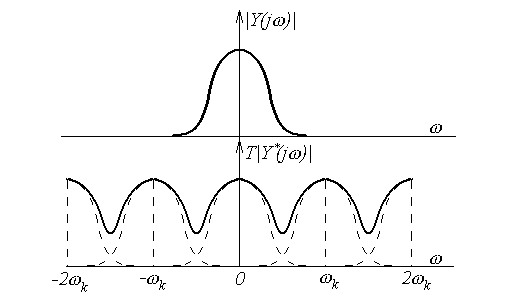
Рис. 59.

Теорема Котельникова (Найквиста)

Позволяет ответить на вопрос: каким должен быть период квантования для того, чтобы по дискретному сигналу можно было точно, без потерь, восстановить исходный непрерывный сигнал.

Поскольку спектр дискретного сигнала есть сумма спектров непрерывного сигнала, сдвинутых на , k=0, 1, 2, … , то восстановить непрерывный сигнал можно только в том случае, если отдельные составляющие спектра дискретного сигнала не накладываются друг на друга (рис. 60). Это условие можно записать в виде:

(150)

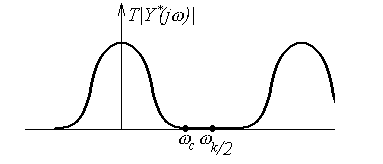
Рис. 60.

где – частота квантования,

_c – частота среза спектра непрерывного сигнала – частота максимальной гармоники, входящей в спектр непрерывного сигнала (Практически _c – это частота, при которой модуль спектра |Y(j)| становится достаточно малым:

,

– малое число.)

При выполнении условия (150), пропустив дискретный сигнал через фильтр с полосой можно выделить неискаженный спектр непрерывного сигнала, т.е. восстановить его без искажений. При невыполнении этого условия отдельные составляющие спектра накладываются друг на друга, и выделить спектр непрерывного сигнала не удается.

Таким образом, непрерывный сигнал, имеющий ограниченный спектр с частотой среза _c, может быть точно восстановлен по дискретному сигналу, если частота квантования _k хотя бы в два раза выше частоты среза _c (или, что то же, если период квантования T хотя бы в два раза меньше периода самой высокочастотной составляющей спектра T_c:

T<T_c/2.

На практике рекомендуется, чтобы период квантования был в раз меньше периода высокочастотной составляющей спектра:

. (151)

Итак, из теоремы Котельникова следует, что мы можем точно восстановить непрерывный сигнал по дискретному, если на одном периоде самой высокочастотной составляющей сигнала укладывается не менее двух ( а лучше ) ординат дискретного сигнала. Если же период квантования не удовлетворяет условию (151), восстанавливая непрерывный сигнал по дискретному, мы не сможем различить высокочастотные составляющие этого сигнала.

Теорема Котельникова позволяет правильно выбрать период квантования при проектировании цифровых систем регулирования.