Решение. Найдем координаты центра масс системы в начальный и конечный моменты и приравняем их, поскольку центр масс остался на одном месте.

За начало координат примем точку, где находился в начальный момент первый человек массой m₁ (рис.10) .

Т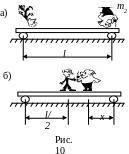 огда Х_С = (m₂ L +ML/2) / (m₁ +m₂ + M) = (m₁L/2 + m₂ (L-X) +ML/2) /(m₁ +m₂ + M), здесь М – масса платформы. Отсюда находим

Х = m₁ L/ 2m₂.

Очевидно, что при m ₁  2m₂ Х L и задача теряет смысл.

Задача 19. На нити, перекинутой через неподвижный блок, подвешены два груза массами m₁ и m₂ (рис. 11) . Найти ускорение этой системы, если блок невесомый, без трения и m₁  m₂.

Решение.

Т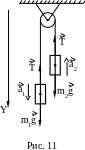 ак как a_Cm =  F_внеш, или (m₁ +m₂) a_C =  F_внеш, то a_C =  F_внеш / (m₁ +m₂),

a_C =( m₁a₁ + m₂ a₂ )/(m₁ +m₂) или в проекциях на ось , направленную вертикально вниз, a_C = ( m₁a₁ + m₂ a₂ )/(m₁ +m₂).

Так как a₁ = - a₂ = a = mg/(m₁ +m₂)=(m₁ - m₂)g/(m₁ +m₂), получаем после подстановки

a_С = (m₁ -m₂)²g/(m₁ +m₂)².

Задача 20. Человек массой m находится на корме лодки массой М, стоящей в пруду. Длина лодки L. На сколько сдвинется лодка относительно берега, если человек перейдет с кормы на нос?

Решение

Т ак как в горизонтальном направлении на систему «лодка-человек» силы не действуют, положение ее центра масс должно сохраняться. Но положение центра масс системы определяется положением центров масс лодки и человека (рис. 12).

Пусть координата центра тяжести системы 0_С относительно центра масс лодки 0_Л первоначально было равно х. Тогда х = m L/2 / (M +m).

Когда человек перейдет с кормы лодки на ее середину, то очевидно, положение его центра масс должно совпасть с положением центра масс системы. Следовательно, и положение центра масс лодки должно совпасть с положением центра масс системы, то есть лодка должна переместиться на расстояние х. На такое же расстояние переместится лодка при переходе человека с ее середины на нос. Следовательно, полное перемещение лодки будет равно Х = 2 х = mL /(M +m).

Примечание. Положение центра тяжести системы рассчитывалось по формуле Х_С =  (m_i x_i ) /  m_i

З адача 21. Снаряд вылетает из орудия со скоростью V₀ под углом  к горизонту. В верхней точке траектории снаряд разрывается на два равных осколка, причем скорости осколков непосредственно после разрыва горизонтальны и лежат в плоскости траектории. Первый осколок упал на расстоянии S от орудия в направлении выстрела. Определить место падения второго осколка, если известно, что он упал дальше первого.

Решение

Так как силы, приведшие к разрыву снаряда, являются внутренними, то на движение центра масс никаким образом не влияют. То есть центр масс системы продолжает двигаться в прежнем направлении, как если бы разрыва не было. Дальность полета его равна l = (V₀² Sin 2) /g. Осколки же упадут на землю одновременно на одинаковом расстоянии от точки предполагаемого приземления центра масс. Поэтому искомое расстояние определяется сразу:

L – S = L – l; отсюда L = 2 l – S.

Еще короче решение в системе отсчета, связанной с центром масс осколков. Так как осколки одинаковы, они упадут симметрично точки предполагаемого приземления центра масс (рис. 13)

Задача 22. От третьей ступени ракеты – носителя, движущейся по орбите вокруг Земли со скоростью V₁, отделяется головная часть массой m₁. С какой скоростью V₂ стала двигаться ракета-носитель, если скорость головной части изменилась на V? Масса ракеты-носителя без головной части М.

Решение. Для решения задачи совершенно неважно, каким способом происходит отделение головной части. Важно только следить за изменением импульса отдельных частей системы. А так как отделение головной части происходит достаточно быстро, то импульсом силы тяжести за время разделения частей ракеты-носителя можно пренебречь.

Предположим, что изменение скорости V параллельно начальной скорости V₁. Тогда для решения задачи достаточно одной оси, например, совпадающей с направлением движения. По закону сохранения импульса

(М + m₁) V₁ = m₁ (V₁ + V) + M V₂ или М V₁ = m₁ V + M V₂.

В проекциях на выбранное направление движения имеем М V₁ = m₁ V + M V₂, откуда находим . V₂ = (М V₁ -m₁ V )/ М.

Если при расчетах окажется, что V₂  0, то после отделения головной части ракета-носитель продолжает двигаться в прежнем направлении. Если же V₂ 0, то после отделения головной части ракета-носитель начинает двигаться в противоположную сторону со скоростью, равной по модулю V₂.

Если же изменение скорости V не параллельно начальной скорости, то задачу решать можно только векторным способом.