3. Комбинационные законы
Комбинационные законы алгебры логики во многом соответствуют комбинационным законам обычной алгебры, но есть и отличия.
A. Закон тавтологии (многократное повторение)
X + X + X + X = X X * X * X * X = X
Этот закон позволяет использовать логические элементы с большим количеством входов в качестве логических элементов с меньшим количеством входов. Например, можно реализовать двухвходовую схему "2И" на логическом элементе "3И", как это показано на рисунке 4:
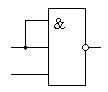Рисунок 4.
Схема "2И-НЕ", реализованная на
логическом элементе "3И-НЕ"
или использовать схему "2И-НЕ" в качестве обычного инвертора, как это показано на рисунке 5:
Рисунок 5.
Схема "НЕ", реализованная на
логическом элементе "2И-НЕ"
Однако следует предупредить, что объединение нескольких входов увеличивает входные токи логического элемента и его ёмкость, что увеличивает ток потребления предыдущих элементов и отрицательно сказывается на быстродействии цифровой схемы в целом.
Для уменьшения числа входов в логическом элементе лучше воспользоваться законом одинарных элементов, как это было показано выше.
b. закон переместительности
A + B + C + D = A + C + B + D
c. закон сочетательности
A + B + C + D = A + (B + C) + D = A + B + (C + D)
d. закон распределительности
X1(X2 + X3) = X1X2 + X1X3 X1 + X2X3 = (X1 + X2)(X1 + X3) = /докажем это путём раскрытия скобок/ = = X1X1 + X1X3 + X1X2 + X2X3 = X1(1 + X3 + X2) + X2X3 = X1 + X2X3
4. Правило поглощения (одна переменная поглощает другие)
X1 + X1X2X3 =X1(1 + X2X3) = X1
5. Правило склеивания (выполняется только по одной переменной)
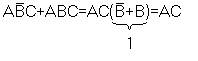
Также как в обычной математике в алгебре логики имеется старшинство операций. При этом первым выполняется:
Действие в скобках
Операция с одним операндом (одноместная операция) — "НЕ" инверсия(-)
Конъюнкция — "И" (*)
Дизъюнкция — "ИЛИ"(+)
Сумма по модулю два.
Операции одного ранга выполняются слева направо в порядке написания логического выражения. Алгебра логики линейна и для неё справедлив принцип суперпозиции.
Построение (запись) логических выражений Каждое сложное (составное) высказывание можно выразить в виде формулы – логического выражения.
В выражение входят:
- логические переменные, которые обозначают высказывания - знаки логических операций, которые обозначают логические функции.
Для составления выражений на языке алгебры логики нужно выделить простые высказывания и логические связки между ними.
Рассмотрим пример логического выражения.
(X * Y = 5 или X * Y = 4 ) И (X * Y ≠ 5 или X * Y ≠ 4)
Подставим в выражение значения x=2, y=2
(2 * 2 = 5 или 2 * 2 = 4) И (2 * 2 ≠ 5 или 2 * 2 ≠ 4)
Выделяем простые высказывания и связки
( A или B ) И (¬A или ¬B )
Запишем выражение логической функции
F = ( A V B ) & (¬A V ¬B )
Подставим в функцию формальные значения высказываний.
F = ( 0 V 1) & (1 V 0) = 1 & 1 = 1 - для данных условий результирующим значением функции является истина
Для выяснения поведений функций в любых ситуациях строят для них таблицы истинности.
Количество проверяемых комбинаций равно 2n
- где n – количество логических переменных.
Рассмотрим следующую функцию: F = ( A V B ) & (¬A V ¬B )
А |
B |
A V B |
¬A |
¬B |
¬A V ¬B |
F |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
Хотя логика работает с формальными логическими выражениями, всегда подразумевается, что эти выражения запись жизненной ситуации, математической задачи, режимов работы электронных или компьютерных устройств и так далее.
Рассмотрим несколько примеров построения логических выражений. Пример 1. Постановка условия: Если придет Вася или Коля и мама разрешит, то пойду гулять. Обозначим :
|
Приход Васи |
A |
|
Приход Коли |
B |
|
Разрешение мамы |
C |
Запишем логическую функцию F = ( A V B ) & C Составим таблицу истинности
A |
B |
A V B |
C |
( A V B ) & C |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
Создание таблицы истинности позволяет рассмотреть все возможные ситуации и получить для каждого случая результирующее значение логического выражения.
Пример 2
Постановка условия: Выбрать из массива нечетные положительные числа Четное число A Нечетное число ¬A Положительное число B
|
Четное число |
A |
|
Нечетное число |
¬A |
|
Положительное число |
B |
F = ¬A Λ B Таблица истинности
A |
¬A |
B |
¬A Λ B |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
Пример 3
Постановка условия: Имеем массив из N целых положительных чисел. Подсчитайте количество четных и нечетных. Если X – четное A Если X – нечетное ¬A Логическая функция F = A V ¬A
A |
¬A |
A V ¬A |
0 |
1 |
1 |
1 |
0 |
1 |
И что же мы имеем? A V ¬A = 1 Дизъюнкция высказывания с инверсией всегда истинна.
Не понятно? посмотри пример конспекте!!!!!!!!!!!!!!!!!!
Базовые логические элементы. Логические (комбинационные) схемы. Минимизация логических функций там же посмотри