Методы расчета радиационного теплообмена
Расчет радиационного теплообмена основан на составлении уравнения теплового баланса для каждого излучающего и поглощающего тела. Для этого необходимо рассчитывать падающие на поверхность тела и излучаемые поверхностью потоки излучения. Способы их расчета зависят от набора предположений о свойствах поверхностей. Наиболее широко в литературе представлен радиационный расчет в предположении, что спектр излучения тел определяется законом Планка, и что поверхности тел отражают излучение диффузно [41, 84, 82, 89, 98, 93, 17, 47, 94, 102, 24, 78, 44, 70, 52, 85, 43, 91, 90, 97, 87, 86, 96]. В этом виде расчета вводится понятие угловых коэффициентов – поглощающихся в телах долей исходящих потоков излучения.
Следует отметить, что единое понятие «угловые коэффициенты» подразделяется на ряд более частных понятий в зависимости от принятых допущений о свойствах поверхностей. В случае расчета теплообмена между серыми диффузными поверхностями поглощенные доли энергии называются в русскоязычной литературе угловыми коэффициентами [85], в англоязычной – view factors [75]. Если при расчете учитывается зеркальное отражение, то в этом случае величина в англоязычной литературе имеет название – extended view factors [75], в русскоязычной литературе устоявшего обозначения данной величины нет. В наиболее сложном случае расчета – при учете и зеркального отражения и пропускания доли поглощенной энергии в русскоязычной литературе называются разрешающие угловые коэффициенты [85], в англоязычной – radiative exchange factors [75]. В настоящей работе все перечисленные понятия упоминаются как угловые коэффициенты с явным указанием принятых допущений.
Расчет значений угловых коэффициентов связан с двойным интегрированием по площадям выражений, зависящих от формы поверхностей, их взаимного расположения и ориентации [47, 93, 98, 5]. Получающиеся интегралы разрешаются в элементарных функциях только для некоторых сочетаний поверхностей, таких например, как «плоскость-плоскость», «двугранный угол», «вложенные сферы». Задача несколько облегчается наличием определенного количества известных решений для некоторых сочетаний поверхностей, но в большинстве случаев возникает необходимость проводить интегрирование численно.
В настоящее время в литературе описаны три основных метода расчета угловых коэффициентов для серых диффузных поверхностей:
- прямое численное интегрирование выражений для угловых коэффициентов,
- геометрические методы,
- методы Монте-Карло.
Исторически первым был предложен и реализован прямой метод, непосредственно следующий из уравнений лучистого теплообмена. Сложность вычислений по этому методу квадратично зависит от количества анализируемых поверхностей. Для получения приемлемой точности необходимо проводить значительное количество вычислений. Из трех описанных методов этот является наиболее ресурсоемким, что обуславливает его небольшое распространение среди современных программных средств расчета радиационного теплообмена.
С геометрической точки зрения угловые коэффициенты лучистого теплообмена между бесконечно малой площадкой и поверхностью конечных размеров представляют собой отношение площади проекции поверхности на полусферу, с центром в центре бесконечно малой площадки, к всей площади полусферы [55], см. Рис. 1.13.
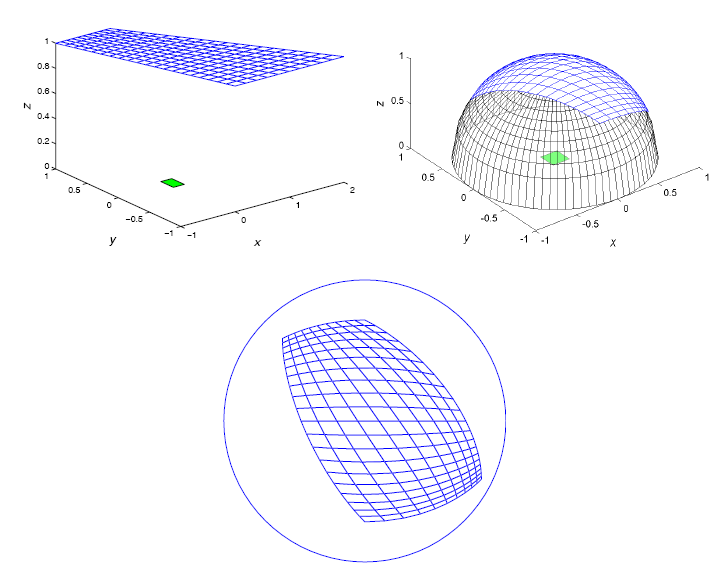
Рис. 1.13. Бесконечно малая площадка и построенная над ней полусфера [75]
Построение проекций поверхностей на полусферу представляет собой ресурсоемкую геометрическую задачу. В тоже время, замена полусферы на более простую геометрическую фигуру позволяет решать задачу проецирования с существенно меньшими затратами.
Методы полусферы [75] основаны на аппроксимации полусферы над площадкой различными геометрическими фигурами: плоскостями, пирамидами, прямоугольными призмами [14] (так называемым полукубом, от английского hemicube), многогранниками, что позволяет упростить построение проекций. Важным моментом при использовании методов полусфер является применение пикселей (от английского pixel, picture element) – дискретов поверхности аппроксимирующей фигуры. Их применение позволяет упростить вычисление доли площади, занимаемой проекцией поверхности на полусфере, построенной вокруг площадки.
Метод Монте-Карло [51, 62] расчета угловых коэффициентов [37, 53, 64, 67, 93] основан на физической сущности процесса радиационного теплообмена. С физической точки зрения угловые коэффициенты между i-ой и j-той поверхностями являются отношением количества фотонов, поглощенных j-той поверхностью, к общему количеству фотонов, излученных i-ой поверхностью. В большинстве случаев число фотонов, излученных поверхностью за единицу времени, является чрезмерно большим для непосредственного моделирования хода каждого фотона. К тому же, в большинстве случаев точный расчет траектории отдельного фотона не возможен в принципе, что приводит к необходимости использовать статистические методы расчета хода излучения. Для этого весь набор фотонов, излученных с заданной поверхности за единицу времени, разбивается на заданное количество групп, пучков, и определяется доля мощности излучения, переносимая каждой группой. Затем для каждого пучка случайным образом выбирается направление излучения и определяется, попадает ли пучок в какую-либо поверхность и если попадает, то в какую именно. Для каждой поверхности ведется учет попавших пучков и определяется суммарная доля полной мощности излучения.
Методы полусферы и Монте-Карло широко используются для создания программных комплексов расчета радиационного теплообмена [2, 8, 1, 71, 26, 74, 27, 39, 73, 72, 34, 54, 69, 46, 3, 92]. Множество таких программ построено на допущениях о телах как серых излучателях и учитывают только диффузный характер отражения. В большинстве комплексов учтена зависимость теплопроводности и теплоемкости от температуры и/или времени. Однако в применении к расчету радиационных экранов, работающих как при комнатных , так и при криогенных температурах, указанные допущения приводят к чрезмерно большой погрешности, что вынуждает отказаться от допущения о планковском спектре излучения тел, учитывать зависимость термооптических свойств от температуры, времени и длины волны падающего излучения и принимать во внимание зеркальное отражение и пропускание излучения элементами конструкции.
Расчету радиационного теплообмена с такими допущениями посвящено несколько меньше работ [59, 93, 75]. Современные программные комплексы при расчете используют разбиение непрерывного спектра излучения на ряд поддиапазонов, отдельно вычисляя ход излучения в каждом поддиапазоне [59]. Кроме того, при учете зависимости термооптических свойств от температуры производится повторное вычисление матрицы угловых коэффициентов, что приводит к увеличению времени счета и не всегда является приемлемым.
Указанные причины вынуждают разрабатывать метод расчета радиационного теплообмена, пригодный для расчета радиационных экранов перспективных космических обсерваторий и создавать на его основе программное обеспечение.
Основными задачами при создании такого метода являются расчет поглощаемых и излучаемых потоков излучения. Потоки излучения, поглощаемые поверхностями тел, могут быть определены с использованием угловых коэффициентов, однако расчет их численных значений в этом случае представляется более сложным, чем в «диффузной-серой» постановке. Необходимо заметить, что при более реалистичной постановке задачи определение угловых коэффициентов должно быть уточнено. Угловые коэффициенты в этом случае – это доли энергии излучающего тела, поглощаемой в других телах (в том числе, и в самом излучающем теле). При этом энергия излучения передается как посредством отражения, зеркального и диффузного, так и посредством пропускания.
Основным отличием такого определения от определения «серой-диффузной» постановки является то, что учитываются более чем одно взаимодействие излучения с веществом. В упрощенной постановке пучок либо сразу после излучения поглощается, либо выходит за пределы рассматриваемой области. В более сложном случае «память» пучка приводит к тому, что текущие свойства пучка, его энергия и направление распространения, являются следствием прошлых взаимодействий с веществом. В этом случае свойства пучка являются функцией от термооптических коэффициентов поверхностей, с которыми он испытал взаимодействие [75]. Соответственно, энергия, поглощаемая в элементах исследуемого объекта, зависит от термооптических свойств всех поверхностей, с которыми испытал взаимодействие пучок. Следовательно, в более реалистичной постановке угловые коэффициенты являются функцией термооптических свойств поверхностей.
Если упрощенная постановка позволяет считать угловые коэффициенты постоянными во время расчета, то необходимость учитывать зависимость термооптических свойств от температуры, времени и длины волны излучения не позволяет этого. Использовать геометрические свойства коэффициентов при построении метода становится затруднительно, так как в этом случае необходимо строить и анализировать граф лучистых потоков между поверхностями, что в случае большого количества поверхностей представляет определенные трудности.
В тоже время физический смысл угловых коэффициентов при усложнении постановки остается неизменным, что позволяет использовать для расчета их численных значений методы статистических испытаний, методы Монте-Карло.