- •Шаенко Александр Юрьевич
- •Введение
- •Тепловой расчет радиационных экранов больших космических телескопов (обзор)
- •Радиационные экраны
- •Методы расчета радиационного теплообмена
- •Статистические методы расчета угловых коэффициентов
- •Использование средств трехмерной графики для расчета угловых коэффициентов
- •Программные комплексы расчета радиационного теплообмена
- •Требования к методу расчета радиационного теплообмена, учитывающему сложные виды взаимодействия и переменные теплофизические и термооптические свойства
- •Расчет радиационно-кондуктивного теплообмена
- •Допущения и предположения
- •Математическая постановка задачи радиационно-кондуктивного теплообмена
- •Расчет испускаемых лучистых потоков
- •Расчет поглощаемых лучистых потоков
- •2.4.1. Расчет точки пересечения пучка с элементами модели
- •2.4.2. Определение вида взаимодействия пучка с элементом
- •2.4.3. Расчет направления распространения пучка после взаимодействия его с элементом
- •2.4.4. Учет поглощения пучка
- •Безматричный распределенный расчет радиационного теплообмена
- •2.5.1. Расчет радиационного теплообмена без использования матрицы угловых коэффициентов
- •2.5.2. Распределенный расчет радиационного теплообмена
- •Расчет кондуктивного теплообмена
- •Метод интегрирования по времени
- •Генератор случайных чисел
- •Программная реализация метода, подтверждение его достоверности и примеры расчетов различных конструкций космической техники
- •Программная реализация метода
- •Подтверждение достоверности и работоспособности метода
- •3.2.1. Радиационный теплообмен
- •3.2.2. Кондуктивный теплообмен
- •3.2.3. Заключение о достоверности разработанного метода расчета
- •Расчеты обсерватории «Миллиметрон»
- •3.3.1. Оценка влияния погрешностей формы экранов на температурный режим зеркала
- •3.3.2. Анализ влияния термооптических свойств покрытий на температуру зеркала
- •3.3.3. Сравнительный анализ двух вариантов конструкции обсерватории
- •3.3.4. Анализ влияния Земли на тепловой режим главного зеркала
- •Заключение
- •Приложение. Краткое описание алгоритма t.H.O.R.I.U.M.
- •Список литературы
3.2.2. Кондуктивный теплообмен
Достоверность реализации расчета кондуктивного теплообмена проверялась на примере стержня и пластины с заданными источниками тепловыделения. Для этого одна и та же задача решалась с помощью программного пакета MathCad и модуля T.H.O.R.I.U.M.
Исследуемый
стержень имел длину 1 м и площадь
поперечного сечения 0.0001 м. Плотность
материала составляла 8960
![]() .
Расчет проводился для двух расчетных
случаев. В первом случае теплоемкость
и теплопроводность материала были
приняты постоянными и составляли 386
.
Расчет проводился для двух расчетных
случаев. В первом случае теплоемкость
и теплопроводность материала были
приняты постоянными и составляли 386
![]() и 401
и 401
![]() соответственно. Во втором случае
теплоемкость и теплопроводность зависели
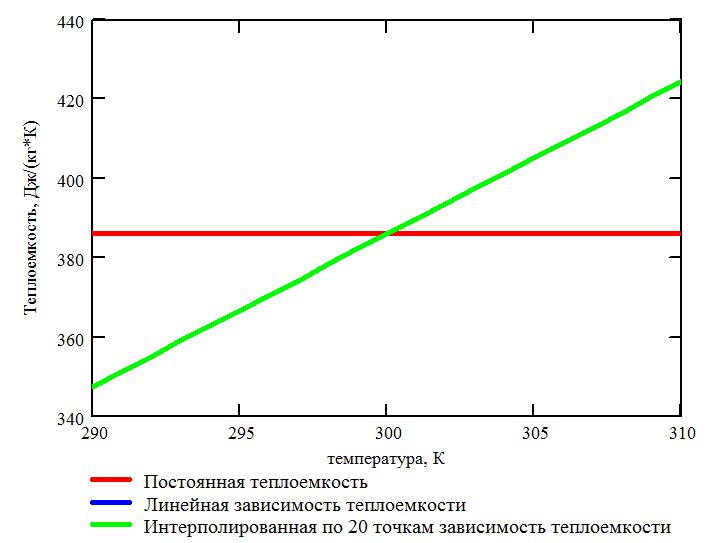
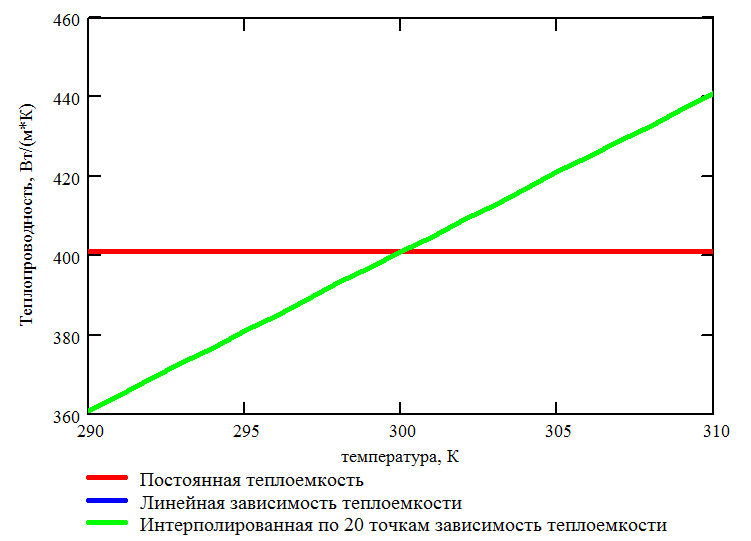
от температуры, см. Рис. 3.26 и Рис. 3.27. В
обоих случаях радиационный теплообмен
не учитывался, степень черноты поверхности
стержня принималась равной 0,0.
соответственно. Во втором случае
теплоемкость и теплопроводность зависели
от температуры, см. Рис. 3.26 и Рис. 3.27. В
обоих случаях радиационный теплообмен
не учитывался, степень черноты поверхности
стержня принималась равной 0,0.
Начальная температура стержня составляла 300К, на левом конце стержня находился источник тепла мощностью 1 Вт, на правом конце – охладитель мощностью -1 Вт.
В T.H.O.R.I.U.M. стержень моделировался 100 элементов типа CHEXA8.
|
|
Рис. 3.26. Зависимость теплоемкости материала стержня от температуры |
Рис. 3.27. Зависимость теплопроводности материала стержня от температуры |
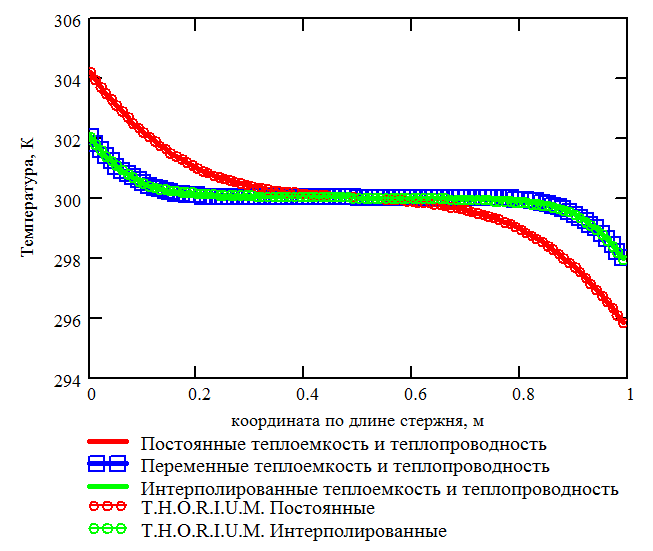
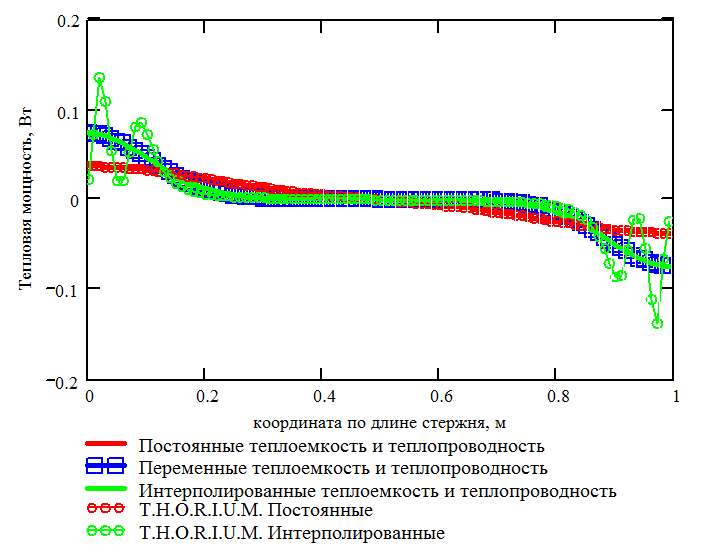
Результаты расчета в обоих случаях изображены на Рис 3.28 и 3.29. Анализ результатов позволяет сделать вывод о совпадении результатов расчета с достаточной степенью точности, что, в свою очередь свидетельствуют о верной реализации расчета кондуктивного теплообмена конструкции, представленной трехмерными конечными элементами.
|
|
Рис. 3.28. Теоретическая и расчетная зависимости температуры по длине стержня от времени |
Рис. 3.29. Теоретическая и расчетная зависимости мощности теплообмена по длине стержня от времени |
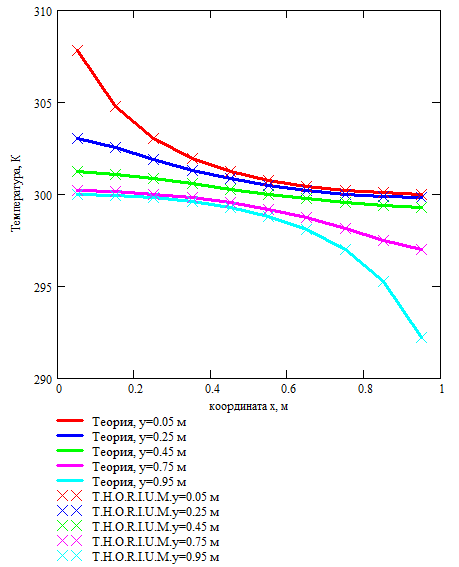
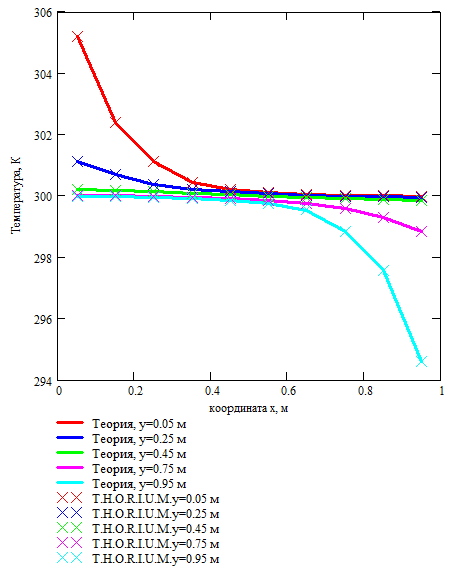
Оценка достоверности расчета теплообмена в пластине проводилась при следующих исходных данных. Размеры пластины 1 м х 1 м, толщина пластины 0,01 м. Плотность материала пластины 8960 . Начальная температура пластины составляла 300К. В одном углу пластины находился источник тепла мощностью 25 Вт, в противоположном по диагонали углу пластины находился охладитель мощностью -25 Вт.
Расчет пластины проводился для трех расчетных случаев: радиационный теплообмен не учитывается, постоянные теплоемкость и теплопроводность 386 и 401 соответственно; радиационный теплообмен не учитывается, теплоемкость и теплопроводность зависят от температуры, см. Рис. 3.26 и Рис. 3.27; учитывается радиационный теплообмен, теплоемкость и теплопроводность зависят от температуры, см. Рис. 3.26 и Рис. 3.27. В том случае, когда учитывается излучение с поверхности пластины, степень черноты принимается равной 1,0, в остальных случаях степень черноты 0,0.
Модель пластины в модуле состояла из 100 элементов типа CQUAD4.
Результаты расчета изображены на Рис. 3.30-3.32.
|
|
Рис. 3.30. Распределения температуры по пластине. Постоянные теплоемкость и теплопроводность. Нет излучения |
Рис. 3.31. Распределения температуры по пластине. Теплоемкость и теплопроводность зависят от температуры. Нет излучения |
На Рис. 3.30-3.32. видно, что температуры, полученные в пакете MathCad и модуле T.H.O.R.I.U.M. достаточно хорошо совпадают. Это позволяет утверждать, что расчет кондуктивного теплообмена в конструкции, представленной двумерными элементами, реализован корректно.
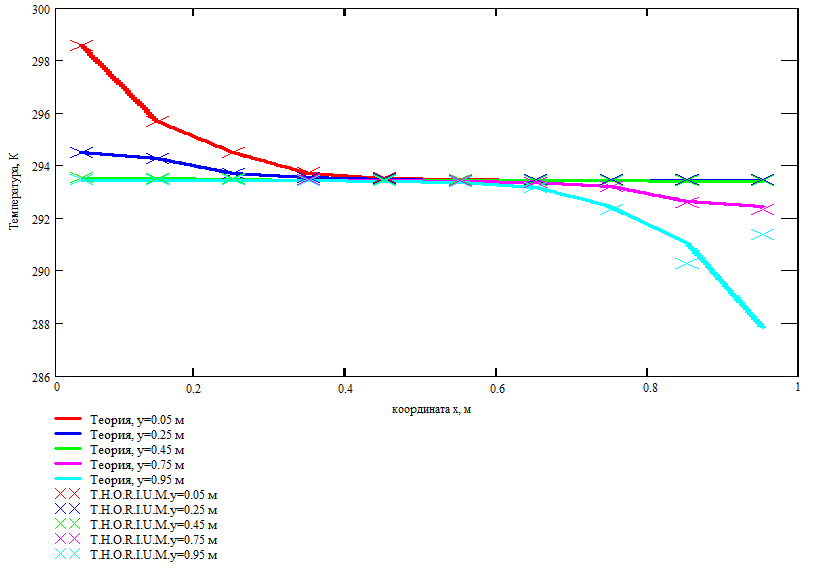
Рис. 3.32. Теоретическая и расчетная зависимости температуры по пластине от времени. Теплоемкость и теплопроводность зависят от температуры. Излучение учитывается