2. Подтверждение достоверности и работоспособности метода

Проверка работоспособности нового метода расчета и адекватность его программной реализации является насущной необходимостью перед началом практического использования метода и в процессе его модернизации. Для проведения проверки необходимо подготовить набор достоверных решений и сравнить с ними результаты расчета по разработанному методу. В случае если результаты различаются незначительно, метод является работоспособным.

Набор решений для сравнения должен состоять из задач, проверяющих основные этапы расчета радиационного и кондуктивного теплообмена.

3.2.1. Радиационный теплообмен

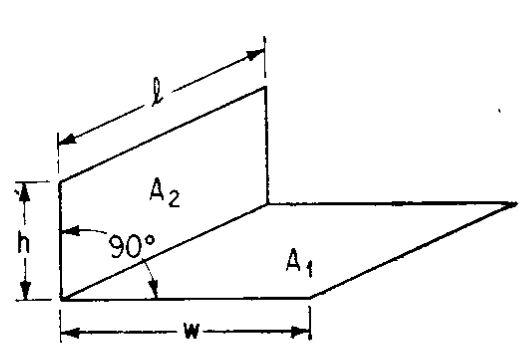
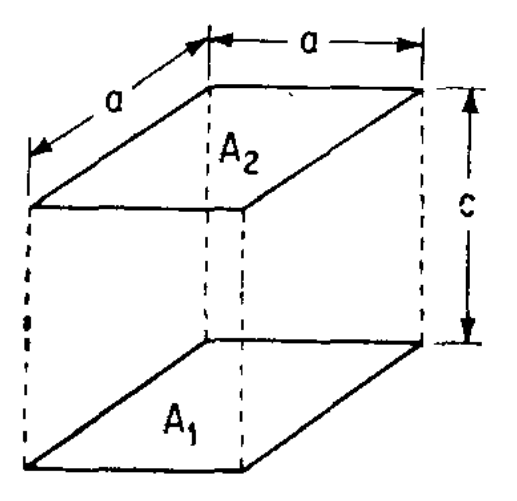
Важнейшим этапом расчета радиационного теплообмена является вычисление угловых коэффициентов. Эталонные решения для проверки этого этапа были взяты из классического труда [93]. Сравнение проводилось для двух конфигураций элементов: две перпендикулярные прямоугольные пластины с общей стороной, см. Рис. 3.2 и две квадратные параллельные пластины размером 1 м х 1 м, см. Рис. 3.3.

Рис. 3.2. Две перпендикулярные прямоугольные пластины с общей стороной	Рис. 3.3. Две квадратные параллельные пластины

Зависимость угловых коэффициентов для перпендикулярных пластин выражается в следующем виде

,

(3.1)

где

, .

,

(3.2)

где

.

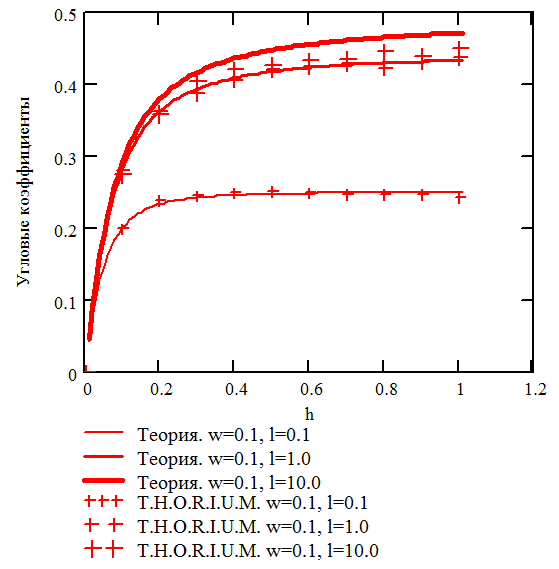
Для получения значений угловых коэффициентов в модуле T.H.O.R.I.U.M. для перпендикулярных пластин использовалось по 10000 пучков фотонов, излучаемых с каждой стороны пластины, для параллельных пластин - по 1000 пучков с каждой стороны пластины. Аналитические и численные зависимости угловых коэффициентов перпендикулярных и параллельных пластин от их геометрических параметров изображены на Рис. 3.3-3.6.

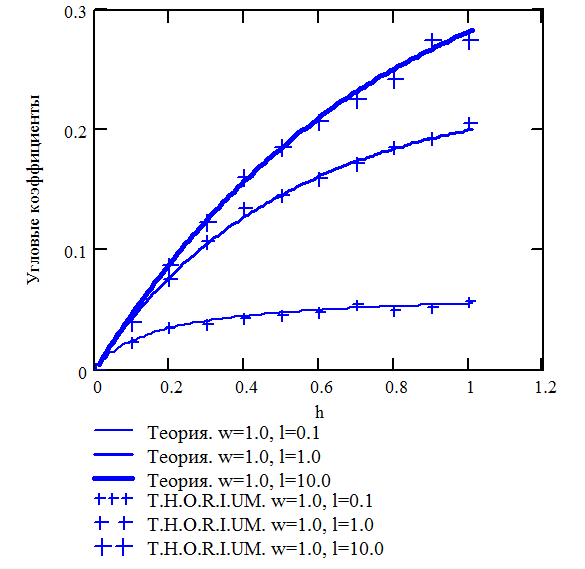
Рис. 3.3. Аналитические и численные зависимости угловых коэффициентов перпендикулярных пластин .	Рис. 3.4. Аналитические и численные зависимости угловых коэффициентов перпендикулярных пластин .
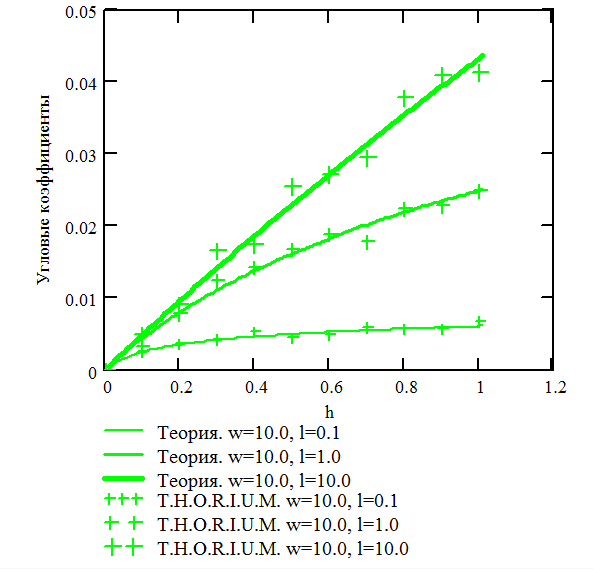
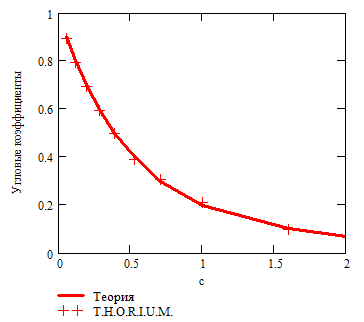
Рис. 3.5. Аналитические и численные зависимости угловых коэффициентов перпендикулярных пластин	Рис. 3.6. Аналитические и численные зависимости угловых коэффициентов параллельных квадратных пластин

На Рис. 3.3-3.6 видно хорошее совпадение между аналитическими и численными результатами. Отсюда следует, что алгоритм расчета угловых коэффициентов реализован верно.

Следующим шагом проверки метода является этап интегрирования полученных теплопритоков. Для этого в программном пакете MathCad аналитически была решена задача охлаждения двух параллельных квадратных пластин размером 1 м х 1 м, выполненных из материала со свойствами, приведенными в Таблицах 3.1. и 3.2. Расстояние между пластинами составляло 0,1 м.

Аналогичная задача была решена в модуле T.H.O.R.I.U.M. с использованием метода интегрирования Эйлера с постоянным и переменным шагом, со сглаживанием и без сглаживания, а также с использованием четырехшагового метода Адамса.

Начальная температура обоих пластин составляла 300К, время интегрирования 100 с.

Таблица 3.1

Теплофизические свойства элементов модели

Материал	Плотность материала,	Удельная теплоемкость,	Теплопроводность,	Толщина, мм
Лавсан с Al	1450	1000	0,24	1

Таблица 3.2

Термооптические свойства элементов модели

Коэффициент зеркального отражения	Коэффициент диффузного отражения	Коэффициент поглощения	Коэффициент пропускания	Степень черноты
0,0	0,0	1,0	0,0	1,0

Полученные зависимости температур и мощностей излучения от времени приведены на Рис. 3.7 и Рис. 3.8.

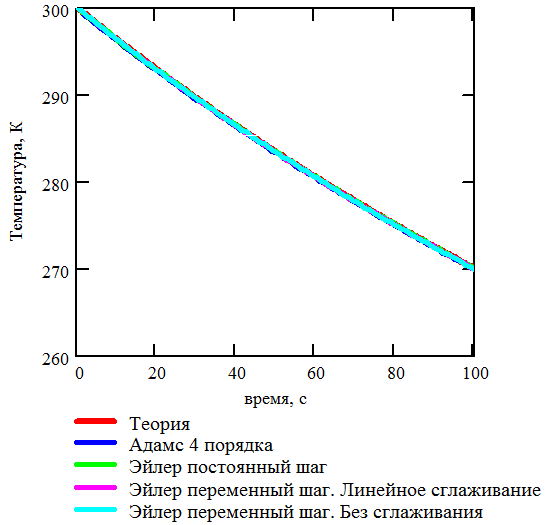
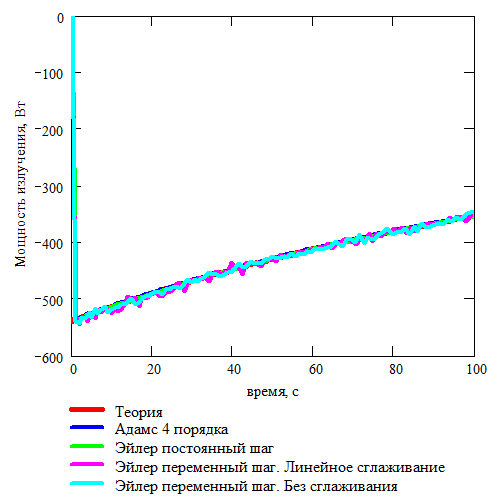
Рис. 3.7. Аналитическая и численные зависимости температуры от времени. Охлаждение параллельных пластин	Рис. 3.8. Аналитическая и численные зависимости мощности излучения от времени. Охлаждение параллельных пластин

На Рис. 3.7 и Рис. 3.8 видно, что аналитическая и численные зависимости температур и мощностей излучения от времени практически совпадают. Это позволяет сделать вывод о том, что описанные методы интегрирования реализованы корректно.

На следующем этапе проверялась правильность работы T.H.O.R.I.U.M. при расчете системы пластины из предыдущей проверки. В этом расчетном случае одна пластина поддерживалась при температуре 300К, а вторая пластина с начальной температурой 200К нагревалась от первой. Время интегрирования составляло 3000 с. Для расчета угловых коэффициентов с каждой пластин излучалось по 1000 пучков фотонов.

Полученные численные зависимости сравнивались зависимостями, полученными с помощью пакета MathCad. Результаты сравнения показаны на Рис. 3.9 и 3.10.

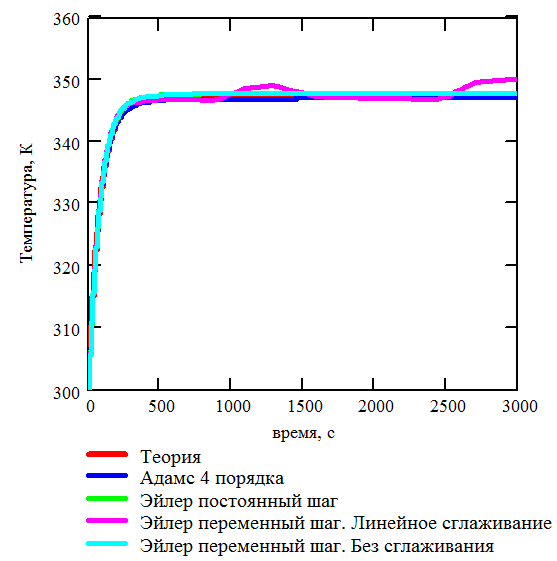
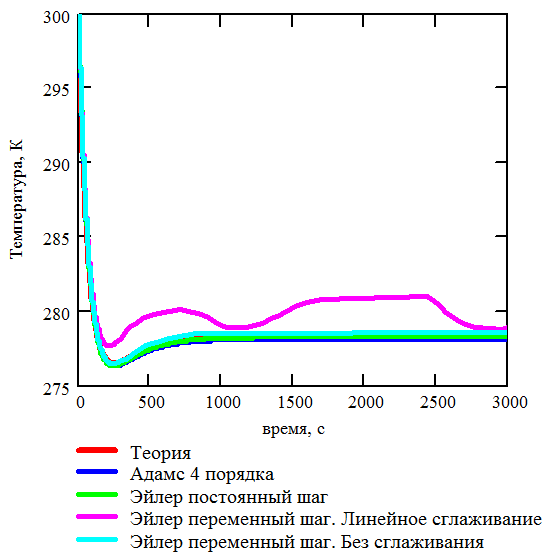
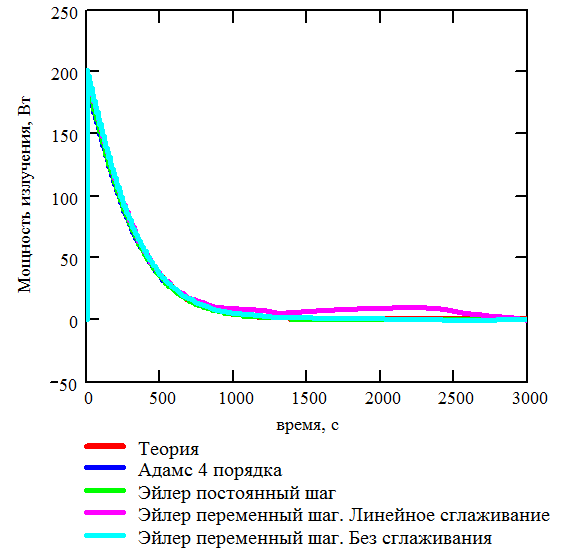
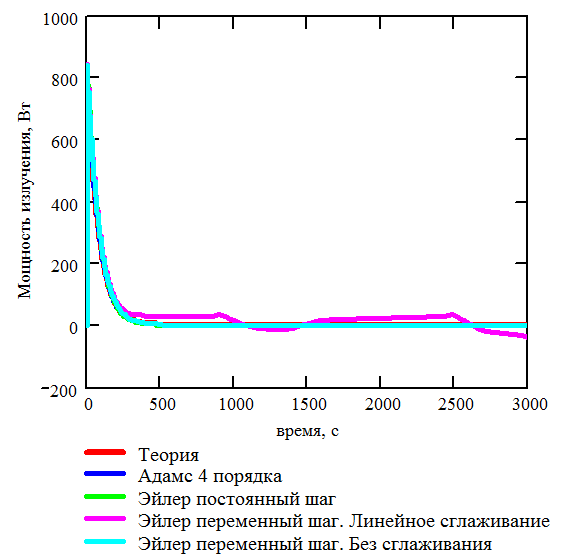
Рис. 3.9. Теоретическая и расчетная зависимости температуры от времени. Одна пластина поддерживается при постоянной температуре	Рис. 3.10. Теоретическая и расчетная зависимости мощности излучения от времени. Одна пластина поддерживается при постоянной температуре

Из анализа Рис. 3.9 и Рис. 3.10 следует, что теоретическая и расчетная температуры второй пластины совпадают с достаточной для практики точностью. Это позволяет утверждать, что 1000 пучков фотонов, излучаемых с каждой стороны пластины достаточно для получения приемлемых результатов. В том случае если необходимо повысить точность расчета, необходимо увеличить количество пучков, излучаемых с каждой стороны пластины.

Важной составляющей разработанного метода расчета теплообмена является точечный источник излучения. Для проверки его работоспособности использованная ранее модель параллельных пластин была модифицирована: начальная температура обоих пластин был принята равной 300К, на одну из пластин перпендикулярно падал лучистый поток плотностью 1374 .

Время интегрирования составляло 3000 с, для расчета угловых коэффициентов с каждой стороны пластины излучалось по 1000 пучков фотонов. Источник испускал 1000 пучков.

Задача решалась с помощью пакета MathCad и модуля T.H.O.R.I.U.M. Результаты расчета представлены на Рис. 3.11-3.14.

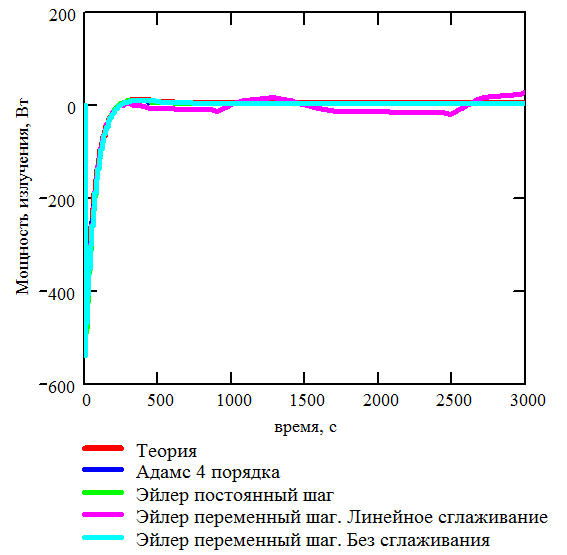
Рис. 3.11. Теоретическая и расчетная зависимости температуры от времени. Освещаемая пластина	Рис. 3.12. Теоретическая и расчетная зависимости мощности излучения от времени. Освещаемая пластина
Рис. 3.13. Теоретическая и расчетная зависимости температуры от времени. Затененная пластина	Рис. 3.14. Теоретическая и расчетная зависимости мощности излучения от времени. Затененная пластина

Полученные результаты позволяют утверждать, что источник излучения в модуле T.H.O.R.I.U.M. реализован правильно.

Простейшей системой с переменными свойствами являются рассмотренные ранее параллельные пластины, выполненные из материала, теплоемкость которого зависит от температуры. Для проверки правильности расчета систем с переменной теплоемкостью эта задача была сначала решена с помощью MathCad, а затем с помощью модуля T.H.O.R.I.U.M.

Теплоемкость материала пластин зависела от температуры следующим образом, см. Рис. 3.15.

Рис. 3.15. Зависимость теплоемкости материала пластин от температуры

Постоянное значение теплоемкости соответствует приведенному выше расчету, в котором одна из пластин поддерживалась при постоянной температуре 300К, а другая, с начальной температурой 200К, нагревалась от нее.

Интерполированная по 20 точкам зависимость теплоемкости от температуры приведена на Рис. 3.15 для оценки точности интерполяции. Как было показано в разделе 2.4.2, в разработанном модуле T.H.O.R.I.U.M. для интерполирования таблично заданных функций используется метод обратных расстояний. Точность интерполяции по этому методу зависит от количества табулированных точек. На Рис 3.15 видно, что исходная линейная и интерполированная зависимости совпадают с достаточной степенью точности.

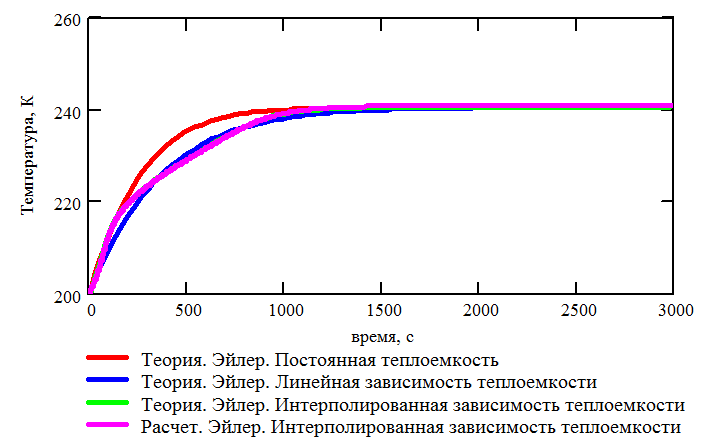
Результаты решения задачи с помощью MathCad и T.H.O.R.I.U.M. приведены на Рис. 3.16 и Рис. 3.17. Анализ теоретического и расчетного решений позволяет сделать вывод об их близости, что, в свою очередь, позволяет утверждать, что расчет систем с переменной теплоемкостью реализован корректно.

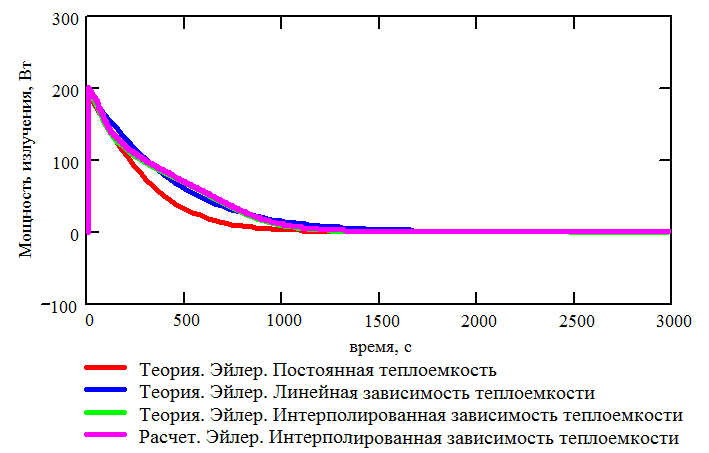
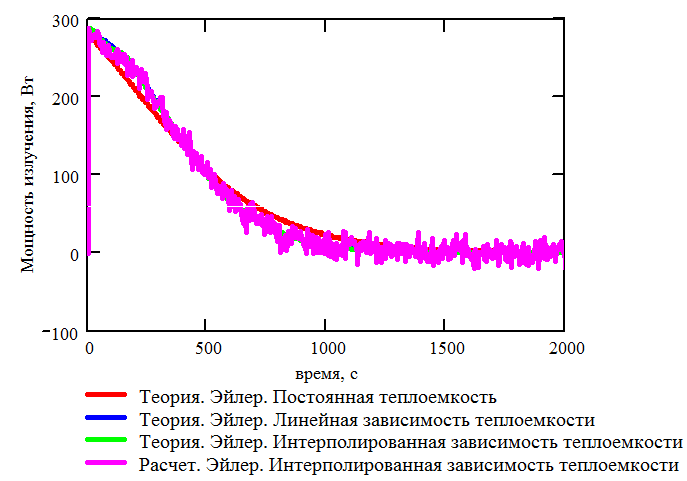
Рис. 3.16. Теоретическая и расчетная зависимости температуры от времени. Теплоемкость зависит от температуры	Рис. 3.17. Теоретическая и расчетная зависимости мощности излучения от времени. Теплоемкость зависит от температуры

Для проверки достоверности реализации расчета радиационного теплообмена в системе параллельных пластин с учетом переменности термооптических коэффициентов были построены две модели. В первой модели коэффициент диффузного отражения, коэффициент поглощения и степень черноты являлись функциями температуры. Во второй модели коэффициент диффузного отражения и коэффициент поглощения зависели от температуры и длины волны падающего излучения, а степень черноты зависела только от температуры. Теплоемкость материала пластин принималась постоянной в соответствии с Табл. 3.1.

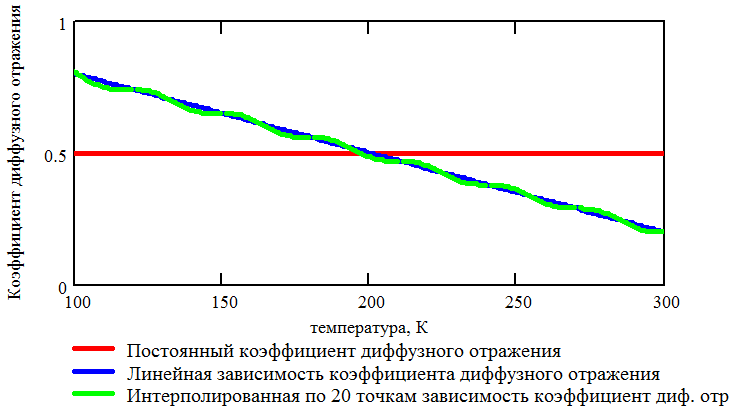
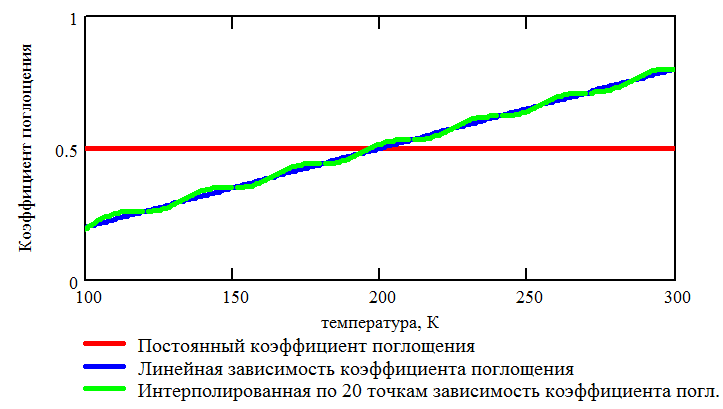
Зависимости коэффициентов диффузного отражения и поглощения от температуры показаны на Рис. 3.18 и Рис. 3.19.

Рис. 3.18. Зависимость коэффициента диффузного отражения от температуры	Рис. 3.19. Зависимость коэффициента поглощения от температуры

Интегрирование проводилось на интервале времени длиной 2000 с. На каждом шаге по времени с каждой из сторон пластин излучалось по 1000 пучков фотонов. Результаты расчета пластин с термооптическими коэффициентами, зависящими от температуры, приведены на Рис. 3.20 и Рис. 3.21.

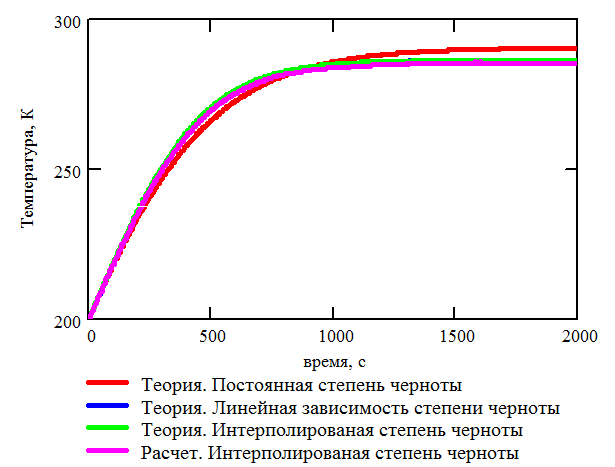
Рис. 3.20. Теоретическая и расчетная зависимости температуры от времени. Термооптические коэффициенты зависит от температуры	Рис. 3.21. Теоретическая и расчетная зависимости мощности излучения от времени. Термооптические коэффициенты зависит от температуры

В более сложном случае термооптические коэффициенты зависят от температуры и длины волны излучения, за исключением степени черноты.

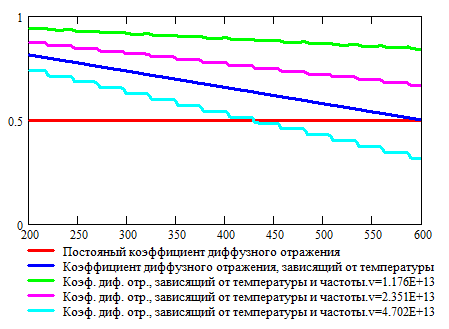
Зависимости коэффициентов диффузного отражения и поглощения от температуры и длины волны падающего излучения приведены на Рис. 3.22 и Рис. 3.23.

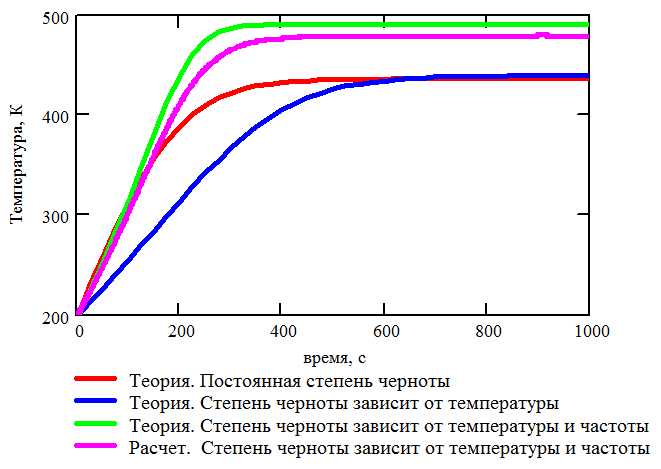
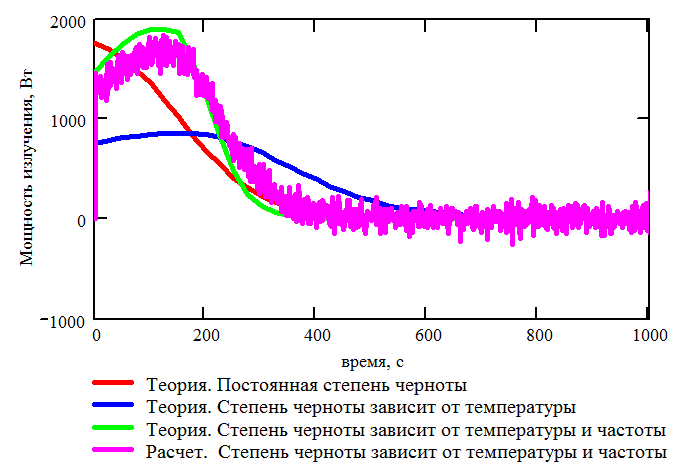
Интегрирование проводилось на интервале времени длиной 1000 с. На каждом шаге по времени с каждой из сторон пластин излучалось по 1000 пучков фотонов. Результаты расчета пластин с термооптическими коэффициентами, зависящими от температуры, приведены на Рис. 3.24 и Рис. 3.25.

Рис. 3.22. Зависимость коэффициента диффузного отражения от температуры и длины волны падающего излучения	Рис. 3.23. Зависимость коэффициента поглощения от температуры и длины волны падающего излучения
Рис. 3.24. Теоретическая и расчетная зависимости температуры от времени. Термооптические коэффициенты зависит от температуры и длины волны падающего излучения	Рис. 3.25. Теоретическая и расчетная зависимости мощности излучения от времени. Термооптические коэффициенты зависит от температуры и длины волны падающего излучения

Анализируя Рис. 3.20, 3.21, 3.24 и 3.25 можно сделать вывод о том, что расчет радиационного теплообмена безматричным способом с учетом зависимости термооптических коэффициентов от температуры и длины волны реализован верно. Кроме того, следует отметить, что учет зависимости термооптических коэффициентов от длины волны позволяет существенно повысить точность расчетов, см. Рис. 3.24.