Расчет кондуктивного теплообмена
Для расчета кондуктивного теплообмена запишем уравнение теплопроводности в точке
|
(2.24) |
,
где
x - точка области, см. рис. 2.1;
t - время;
- температура в точке x;
- удельная теплоемкость в точке x в момент времени t при температуре T;
- плотность в точке x;
-
теплопроводность в точке x
в момент времени t
при температуре
T.
С учетом принятого допущения о равномерном распределении температуры по элементу правую часть уравнения (2.24) для i-го элемента можно переписать в следующем виде
|
(2.25) |
,где
-
количество соседних элементов, имеющих
общие грани с i-м
элементом;
j-й элемент - j-й соседний элемент i-ого элемента, имеющий с ним общую грань;
-
средняя теплопроводность между центрами
i-ого
и j-ого
элементов в момент времени t
при температурах элементов
и
соответственно;
,
- расстояния от общей грани до центров
i-ого
и j-ого
элементов соответственно;
-
расстояние между центрами i-ого
и j-ого
элементов;
-
площадь грани, общей для i-ого
и j-ого
элементов.
Средняя
теплопроводность между центрами i-ого
и j-ого
элементов
рассчитывается по формуле
|
(2.26) |
,где
,
- теплопроводности
i-ого
и j-ого
элементов.
Необходимо
отметить, что расстояние
между центрами i-ого
и j-ого
элементов необходимо рассчитывать
вдоль пути теплопередачи как сумму
расстояний от центра одного элемента
до общей грани и от общей грани до центра
другого элемента, см. Рис. 2.13.
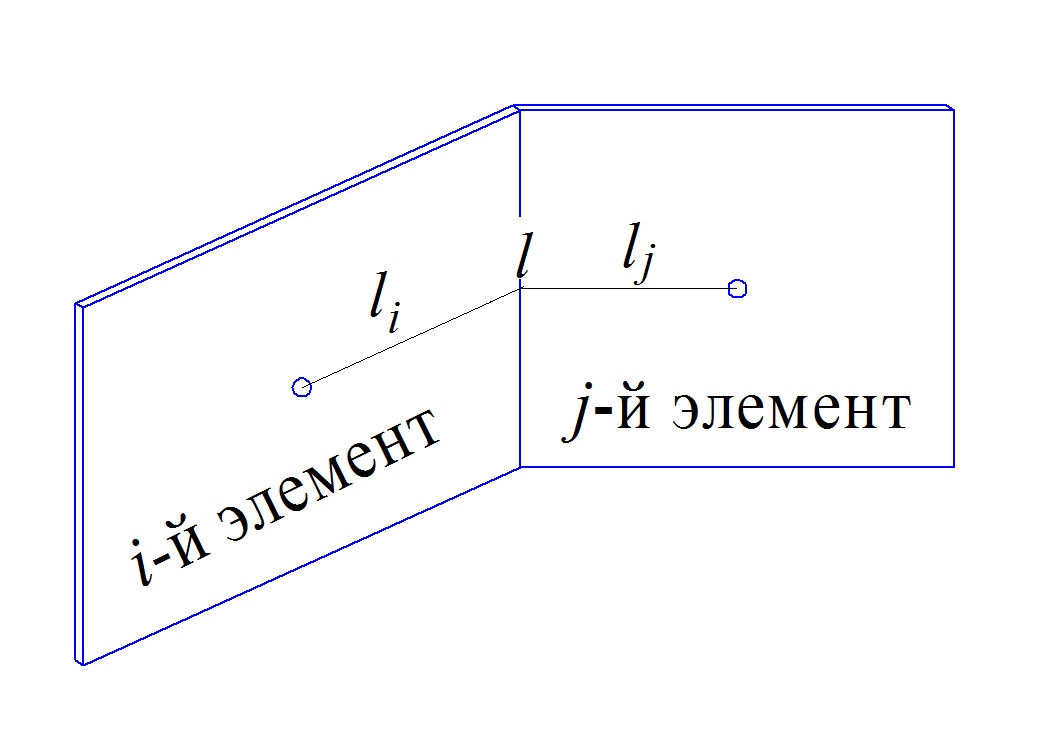
Рис. 2.13. Расстояние между центрами i-ого и j-ого элементов
Фактически, выражения (2.25)-(2.26) реализуют метод тепловых балансов для расчета кондуктивного теплообмена [81].
Используя выражения (2.25) и (2.26), можно рассчитать мощность, выделяющуюся в i-ом элементе за счет кондуктивного теплообмена с соседними элементами. Радиационная часть тепловой мощности, приходящейся на элемент, была определена ранее в выражениях (2.6), (2.9), (2.21) и (2.23). Мощность тепловыделения источников из уравнения (2.4) задана в явном виде. Следовательно, все составляющие полной мощности, приходящейся на элемент на одном шаге по времени, вычислены. На следующем этапе расчета необходимо разработать метод интегрирования по времени.
Метод интегрирования по времени
Наиболее простым метод численного интегрирования обыкновенного дифференциального уравнения является метод Эйлера. Метод является явным, одношаговым, основан на представлении искомой функции в кусочно-линейном виде. Если представить уравнение теплового баланса в i-ого элемента (2.4) в виде
|
(2.27) |
,где
-
полная мощность, приходящаяся на элемент
на одном шаге по времени,
являющаяся суммой радиационной, кондуктивной и заданной частей
|
(2.28) |
,то метод Эйлер можно записать в виде
|
(2.29) |
,где
,
- температура i-ого
элемента на n-ом
и n+1-ом
шагах по времени;
,
- теплоемкости
i-ого
элемента на n-ом
и n+1-ом
шагах по времени;
-
задаваемый шаг по времени;
-
полная мощность, приходящаяся на элемент
на n-ом
шаге по времени.
В случае учета зависимости теплоемкости от температуры, уравнение (2.29) решается методом Ньютона, в случае постоянной теплоемкости его можно переписать следующим образом
|
(2.30) |
,и получать температуру на следующем шаге в явном виде.
Очевидно,
что обеспечить меньшую погрешность
решения можно с использованием метода
интегрирования более высокого порядка,
чем метод Эйлера. Одним из наиболее
широко используемых методов интегрирования
является метод Рунге-Кутты четвертого
порядка [100], представляющий решение
уравнения в виде полинома четвертой
степени. Отличительной чертой метода
является необходимость вычисления
правой части уравнения (2.27) при трех
дополнительных значениях температуры,
распределенных между
и
,
что в случае проведения расчета
радиационного теплообмена безматричным
способом вынуждает проводить дополнительные
циклы статистических испытаний. Это
существенно увеличивает время расчета
и является неприемлемым. Несколько
менее распространенный метод Адамса
[100] позволяет получать решение с тем же
порядком погрешности, что и метод
Рунге-Кутты, но при этом не требует
проводить дополнительные статистические
расчеты. По методу Адамса решение
строится на основе информации о нескольких
предыдущих шагах интегрирования.
Следует отметить, что применение неявных методов интегрирования для решения задачи ограниченно теми же причинами, что и применение метода Рунге-Кутты. Неявные методы интегрирования связаны с решением системы нелинейных уравнений, правая часть которых не выражается аналитически и вычисляется методом Монте-Карло. При решении системы потребуется проводить дополнительные статистические расчеты правой части, что представляется излишне избыточным и ресурсозатратным.
Таким образом, рациональным является интегрирование дифференциального уравнения (2.27) четырехшаговым явным методом Адамса с постоянным шагом, реализованным в следующем виде [100]:
|
(2.31) |
,где
…
-
полная мощность, приходящаяся на i-й
элемент на n-ом,
n−1-ом,
n−2-ом,
n−3-ом
шагах по времени.
Аналогично методу Эйлера, в случае переменой теплоемкости уравнение (2.31) записывается в виде
|
(2.32) |
,и решается методом Ньютона. Когда теплоемкость принимается постоянной, температуру на следующем шаге можно получить в явном виде
|
(2.33) |
.На первом, втором и третьем шагах применить четырехшаговый метод Адамса не представляется возможным. Для расчета температуры на этих шагах необходимо применить метод Эйлера, двух- и трехшаговые методы Адамса соответственно [100]:
|
(2.34) |
,
.Описанные методы интегрирования являются универсальными математическими методами интегрирования, пригодными для решения обыкновенных дифференциальных уравнений общего вида. Учет специфики задачи радиационно-кондуктивного теплообмена позволяет предположить вид искомой функции и тем самым повысить скорость решения задачи.
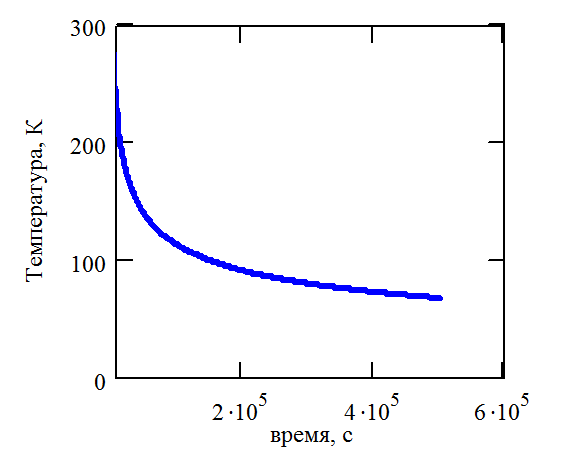
Действительно, характерные зависимости температуры от времени состоят из участков, имеющих вид монотонно возрастающих или убывающих кривых, см. Рис 2.14.
|
|
Рис. 2.14. Примеры решения задачи радиационно-кондуктивного теплообмена. Зависимости температур от времени |
|
Особенностью значительной части решений является существенное различие скорости изменения температуры на различных участках интервала времени интегрирования, что оказывает сильное влияние на размер шага интегрирования. В области решения с большой скоростью изменения температуры шаг интегрирования должен быть выбран меньше чем в области с меньшей скоростью для того, чтобы сохранить сходимость и величину погрешности решения.
Таким образом, наиболее подходящим для решения задач теплообмена с существенно различающимися скоростями изменения температуры на различных участках является метод интегрирования с переменным шагом, например, метод Эйлера, так как в силу описанных недостатков использование метода Рунге-Кутты с переменным шагом затруднено, а метод Адамса с переменным шагом является излишне громоздким.
Критерием
выбора величины шага является скорость
изменения температуры элемента. Величина
допустимого изменения температуры за
один шаг задается в виде коэффициентов
уменьшения и увеличения температуры
за шаг
и
.
Выбор размера шага производится
следующим образом:
рассчитываются входящие тепловые мощности для всех элементов модели,
для каждого элемента вычисляются величины:
-
,(2.35)
,
где
-
шаг при охлаждении элемента,
-
шаг при нагреве элемента,
,
- коэффициенты уменьшения и увеличения
температуры за шаг соответственно,
- текущая температура на n−1-ом шаге по времени,
-
полная мощность, приходящаяся на элемент
на n−1-ом
шаге по времени,
- удельная теплоемкость на n−1-ом шаге по времени,
-
плотность,
-
объем,
в качестве текущего шага
выбирается наименьший положительный
шаг из
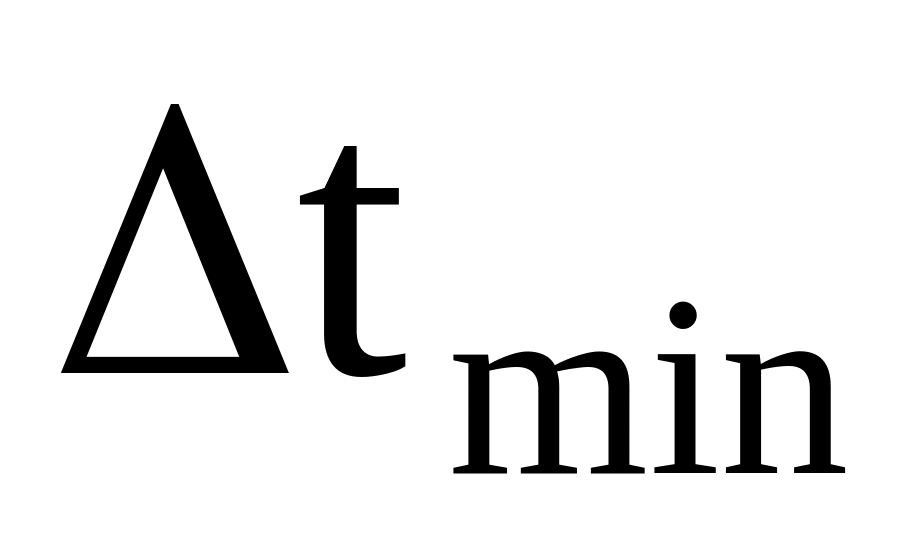и
для
всех элементов модели.
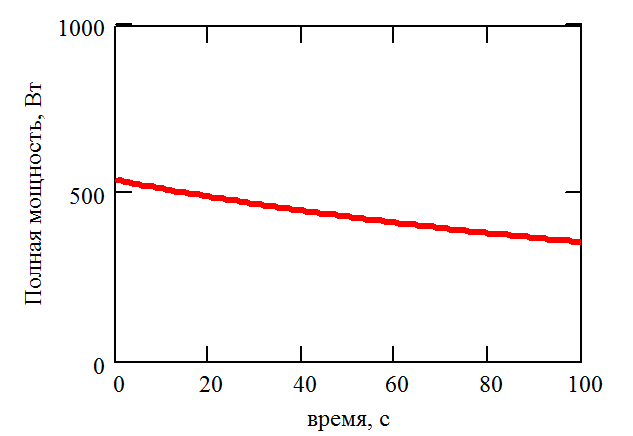
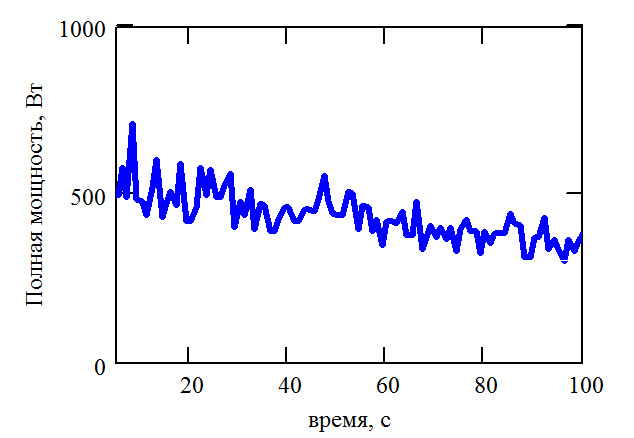
Дополнительный прирост производительности можно получить, приняв во внимание статистический характер расчета полной мощности, приходящейся на элемент. В подавляющем большинстве случаев теоретическая зависимость полной мощности элемента от времени имеет вид гладкой кривой, см. Рис. 2.15, в то время как расчетная зависимость, полученная методом статистических испытаний, имеет отклонения от теоретической зависимости, см. Рис. 2.16.
|
|
Рис. 2.15. Пример теоретической зависимости полной мощности элемента от времени |
Рис. 2.16. Пример зависимости полной мощности элемента от времени, полученной методом статистических испытаний |
Анализируя Рис. 2.15 и 2.16, можно заключить, что зависимость полной мощности элемента от времени, полученная статистическим способом является «зашумленной» теоретической зависимостью. При интегрировании отдельные всплески на Рис. 2.16 требуют значительного уменьшения шага интегрирования для сохранения точности решения, что приводит к увеличению общего количества шагов и времени расчета.
Отсюда следует, что устранение статистических шумов решения позволяет существенно уменьшить общее количество шагов по времени и повысить производительность расчета.
В настоящей работе устранение всплесков производится линейным сглаживанием по заданному количеству шагов.
Алгоритм
сглаживания использует в качестве
исходных данных количество шагов для
сглаживания
.
Сглаживание производится следующим
образом:
первые
шагов полная мощность элемента поступает
в интегратор без сглаживания,на всех последующих шагах значения мощности корректируются по следующей формуле
-
,(2.36)
где
-
скорректированная полная мощность для
i-го
элемента n-ом
шаге,
-
момент времени на начало n-ого
шага,
- вектор коэффициентов прямой сглаживания, причем
-
,
,
,
,(2.37)
скорректированные по формуле (2.36) значения мощностей подаются на вход интегратора
|
(2.38) |
,где
-
текущее значение шага интернирования,
рассчитанное по формуле (2.35),
- скорректированное значение полной мощности для i-го элемента n-ом шаге интегрирования.
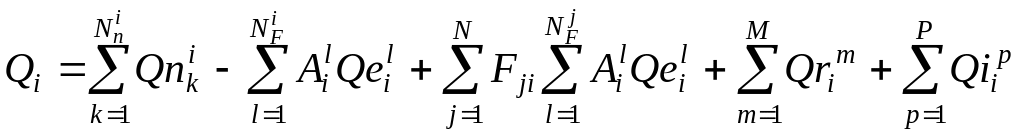