2.4.2. Определение вида взаимодействия пучка с элементом

После того, как стали известны координаты точки пересечения пучка с элементом, становится возможным определить, какой вид взаимодействия происходит между пучком и поверхностью элемента.

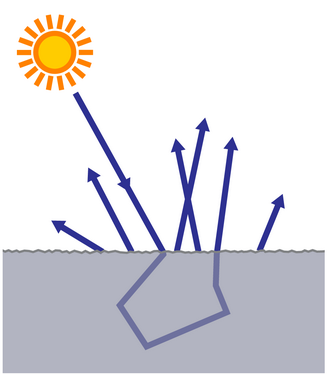
В общем случае направление распространения пучка после взаимодействия с элементом определяется с помощью двунаправленной функции рассеивания BSDF (Bidirectional scattering distribution function) [103, 101] – зависимости, связывающей доли энергии, отражаемые и пропускаемые в различных направлениях, с направлением падения излучения и его длиной волны. В самой общей постановке пучок может выходить из материала не обязательно в том же месте, где произошло взаимодействие, и преломляться без соблюдения закона Снелла. Примерный вид пучка до и после взаимодействия, описанного двунаправленной функцией рассеивания, показан на Рис. 2.9.

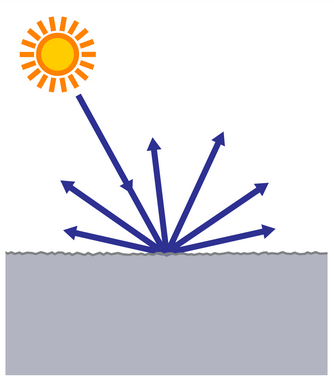
В более упрощенной форме взаимодействие пучка и элемента можно описать, разделив BSDF на двунаправленную функцию отражения BRDF (Bidirectional reflectance distribution function) и двунаправленную функцию пропускания BTDF (Bidirectional transmittance distribution function). В этом случае процессы преломления и пропускания происходят независимо. Примерный вид пучка до и после взаимодействия, описанного двунаправленной функцией отражения, показан на Рис. 2.10.

На практике при проведении расчетов лучистого теплообмена описание взаимодействия пучка с элементом еще более упрощается. Принимается, что излучение взаимодействует с веществом посредством зеркального (подчиняющегося законам геометрической оптики) и диффузного отражения, пропускания и поглощения. С учетом принятых предположений о том, что пропускание излучения возможно только двумерными элементами исследуемой системы, приходим к выводу о том, что процесс взаимодействия излучения с элементом можно описать четырьмя коэффициентами: зеркального отражения, диффузного отражения, пропускания и поглощения.

Рис. 2.9. Вид пучков при использовании двунаправленной функции рассеивания BSDF

Рис. 2.10. Вид пучков при использовании двунаправленной функции отражения BRDF

Для проведения расчета необходимо определить актуальные значения коэффициентов отражения, пропускания и поглощения для текущих температуры элемента, времени,  длины волны и углов падения излучения. В нашем случае, зависимости термооптических коэффициентов задаются таблично.

Определить актуальные значения функции, заданной таблично, можно с привлечением метода обратных расстояний [42, 66], определяемого следующим образом:

,

(2.14)

где

- значение функции в искомой точке ,

- значения функции в известных точках ,

- расстояние между и ,

- заданный показатель степени.

Существенным преимуществом метода обратных расстояний является возможность интерполяции функции между неупорядоченным набором точек. Эта особенность может быть полезна при использовании в расчете экспериментальных данных, обрабатываемых естественным образом без предварительного упорядочивания. Еще одним преимуществом метода является его относительная простота в сравнении с методами так называемого кригинга и радиальных базисных функций.

Описанные преимущества метода позволяют применять его для вычисления актуальных значений функций, задаваемых таблично, и используемых в настоящей работе.

При расчете значений термооптических характеристик выражение для расстояния выглядит следующим образом:

,

(2.15)

где

, , , - температура в искомой точке, в известной точке, наибольшая и наименьшая температура среди всех известных точек;

, , , - значение времени в искомой точке, в известной точке, наибольшее и наименьшее значения времени среди всех известных точек;

, , , - частота излучения в искомой точке, в известной точке, наибольшая и наименьшая частоты среди всех известных точек;

, , , - азимутальный угол в искомой точке, в известной точке, наибольшее и наименьшее значения азимутального угла среди всех известных точек;

, , , - угол места в искомой точке, в известной точке, наибольшее и наименьшее значения угла места среди всех известных точек.

Если величина не зависит от какого-либо параметра, то этот параметр исключается из вычисления расстояния между точками. Например, если величина не зависит от температуры, то тогда принимается .

Актуальные значения термооптических коэффициентов определяют вероятность того или иного вида взаимодействия. Для того, чтобы определить происходящий вид взаимодействия необходимо:

• задать произвольный интервал для генерации случайных чисел, например интервал OD [0;1];

• разбить интервал OD на отрезки, пропорциональные величинам термооптических коэффициентов. Например, если для актуальных температуры, времени, длины волны и углов падения коэффициент зеркального отражения составляет , диффузного отражения , коэффициент пропускания равен 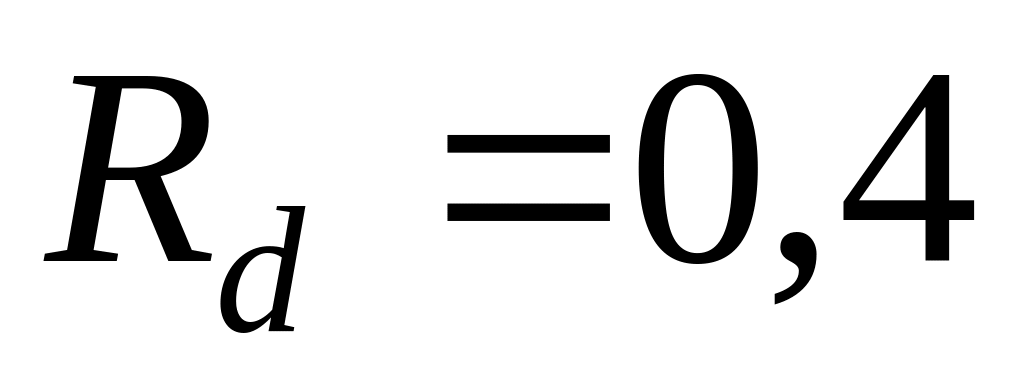и коэффициент поглощения , то полный интервал [0;1] необходимо разбить на следующие подынтервалы 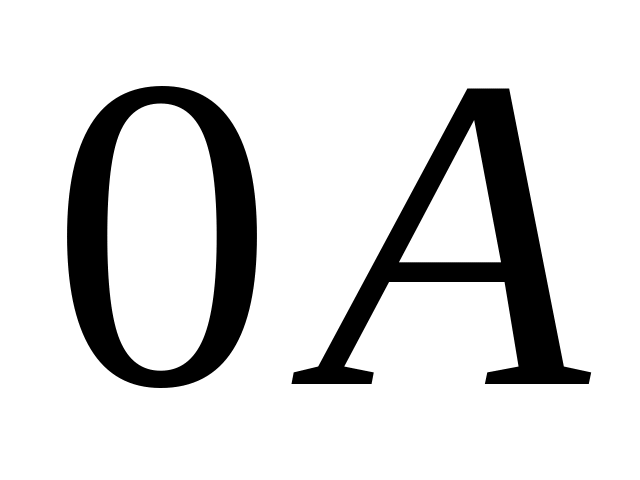[0;0,2), 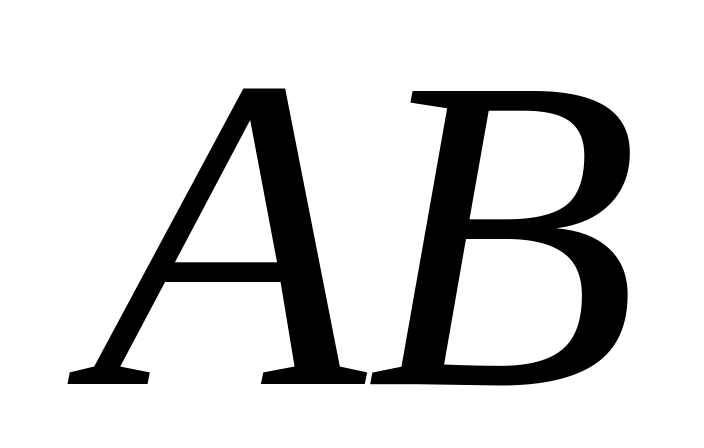[0,2;0,5), 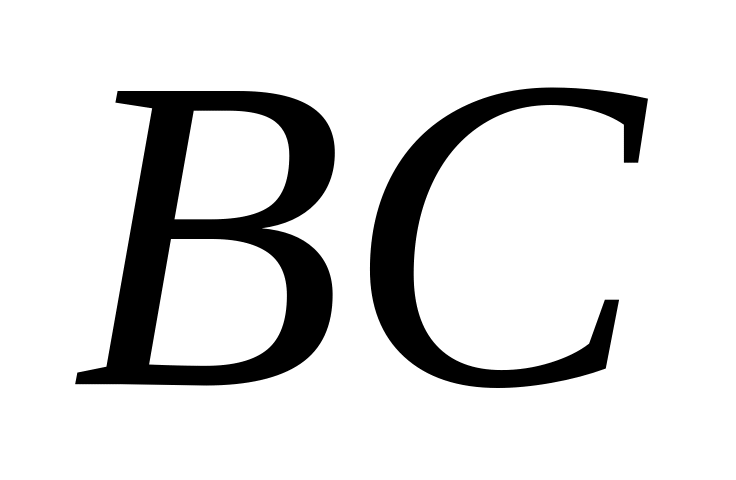[0,5;0,9) и [0,9;1,0] соответственно, см. Рис. 2.11;

• определить конкретный вид взаимодействия путем генерации случайного числа на интервале OD. В случае если случайное число попадает в подынтервал , то считается, что пучок зеркально отражается, если число попадает в подынтервал , то пучок считается отраженным диффузно и т.д.

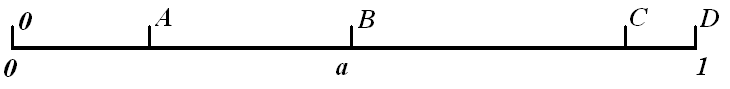
Рис. 2.11. Интервал OD и подынтервалы для определения вида взаимодействия

После того, как определен вид взаимодействия пучка, необходимо рассчитать направление его дальнейшего распространения или провести учет его поглощения.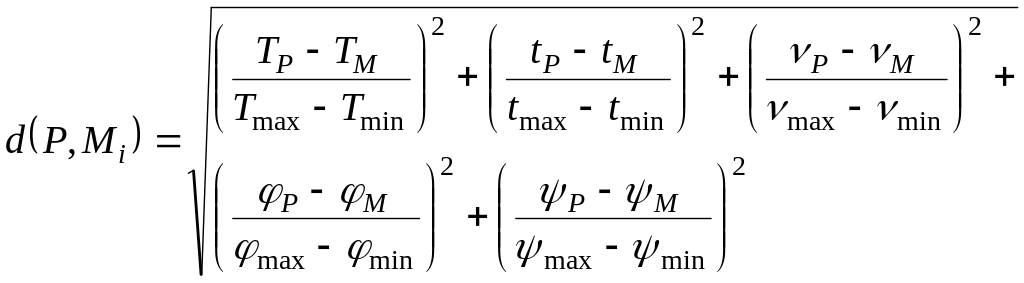