Расчет испускаемых лучистых потоков
Тепловое излучение – электромагнитное излучение, испускаемое веществом, возникающее за счет внутренней энергии тела и имеющее непрерывный спектр. В простейшем случае, при использовании модели абсолютно черного тела (АЧТ), спектр теплового излучения описывается законом Планка [93]:
|
(2.5) |
,где
-
мощность излучения с единицы площади
поверхности в диапазоне частот излучения
от
до
при температуре
,
-
постоянная Планка,
-
скорость света в вакууме,
-
постоянная Больцмана.
Зависимость (2.5), представленная в графическом виде, имеет следующий вид (Рис. 2.1).
Рис. 2.1. Спектры излучения абсолютно черного тела при различных температурах
Поток теплового излучения c поверхности абсолютно черного тела на всех частотах рассчитывается в соответствии с законом Стефана-Больцмана:
|
(2.6) |
,где
-
мощность излучения с единицы площади
поверхности, находящейся при температуре
,
на всех частотах,
.
Используя квантово-механический подход к описанию процесса испускания и поглощения излучения, можно получить вероятностную математическую постановку задачи радиационного теплообмена.
С
точки зрения квантовой теории процесс
излучения представляет собой процесс
испускания квантов электромагнитной
энергии, фотонов. Спектр излучения
определяет распределение плотности
вероятности излучения фотона определенной
частоты: чем выше интенсивность излучения
на определенной частоте, тем выше
вероятность излучения фотона этой
частоты. Зависимость плотности вероятности
излучения фотона
от частоты и температуры можно получить,
разделив выражение (2.5) на поток теплового
излучения на всех частотах (2.6):
|
(2.7) |
.Более удобным для использования является запись распределения вероятностей в кумулятивной форме. Для этого необходимо проинтегрировать выражение (2.7) по частоте следующим образом:
|
(2.8) |
.Полученное выражение представляет собой кумулятивное распределение вероятности излучения фотона от частоты и температуры. Вид зависимости представлен на Рис.2.2.
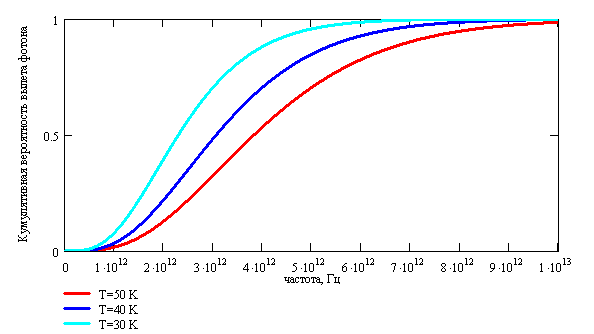
Рис. 2.2. Кумулятивное распределение вероятности излучения фотона в зависимости от частоты и температуры АЧТ
Имея набор случайных чисел, равномерно распределенных на отрезке [0;1] и выражение (2.8), становится возможным получить распределение частот излучаемых фотонов, соответствующее спектру абсолютно черного тела при заданной температуре. Для этого случайные числа подставляют в левую часть выражения (2.8) и находят соответствующее им значение частоты.
Проведя аналогичные выкладки для серого тела, заключаем, что кумулятивное распределение вероятности излучения фотона для серого тела в точности совпадет с выражением (2.8), записанным для абсолютно черного тела. Это объясняется тем, что выражение (2.8) является отношением интеграла интенсивности излучения к полному потоку излучения. И интенсивность, и полный поток линейно зависят от степени черноты, поэтому их отношение от степени черноты не зависит.
Подход,
примененный для построения кумулятивного
распределения, в случае излучающего
абсолютно черного тела, может быть
применен и для расчета кумулятивного
распределения в случае спектра
произвольного вида. Для этого необходимо
выполнить следующую последовательность
действий с известным непланковским
спектром излучения
:
провести интегрирование спектра
по всем частотам и получить аналог
выражения (2.6):
,(2.9)
разделить на
и проинтегрировать получившееся
выражение по частоте:
|
(2.10) |
,Выражение (2.10) пригодно для построения частотного распределения фотонов излучения, соответствующего заданному спектру .
Помимо частоты фотоны также характеризуются направлением распространения. В простейшем случае, фотоны излучаются равномерно во все стороны. Равномерно распределенные угловые координаты получаются по методу Маллея [48] следующим образом:
вокруг точки-центра излучения строится полусфера единичного радиуса;
полусфера параллельно проецируется на излучающую поверхность;
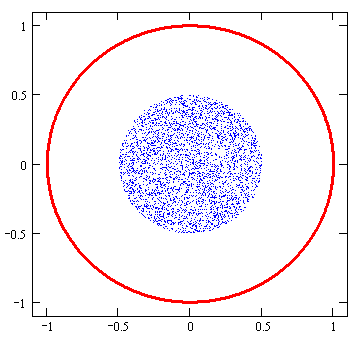
на проекции случайным образом распределяются точки, см. Рис. 2.3;
точки с круга параллельно проецируются обратно на полусферу, см. Рис. 2.4;
направлением излучения фотона является вектор, соединяющий центр окружности с точкой на полусфере.
Рис. 2.3. Точки, случайным образом распределенные по кругу
|
Рис. 2.4. Проекции точек на полусферу
|
В случае необходимости учета неравномерности излучения фотонов метод Маллея необходимо модифицировать. В частности, учет неравномерности может быть произведен изменением распределения точек по кругу. Выбирая неравномерное распределение точек по кругу, можно получить неравномерное распределение направления излучения фотонов, см. Рис. 2.5 и Рис. 2.6.
Рис. 2.5. Точки с неравномерным распределением по кругу |
Рис. 2.6. Неравномерное распределение точек на полусфере |
Неравномерное распределение фотонов в настоящей работе используется для расчета лучистых потоков от внешних источников излучения. Из принятых допущений о точечном характере внешних источников излучения и равномерном испускании ими фотонов во все стороны на первый взгляд следует, что угловое распределение фотонов требуется выбрать аналогичным Рис. 2.3, но спроецированным на полную единичную сферу. Однако данное распределение эффективно только при небольшом расстоянии между исследуемой системой и источником излучения. В случае, когда расстояние между системой и источником велико по сравнению с размерами системы и, следовательно, площадь проекции системы на единичную сферу (см. Рис. 1.12) мала, число фотонов, испускаемых источником в направлении системы, также мало. При равномерном распределении число фотонов излучаемых в направлении системы, квадратично уменьшается с увеличением расстояния между системой и источником. При большом расстоянии большая часть фотонов источника гарантированно не облучает систему.
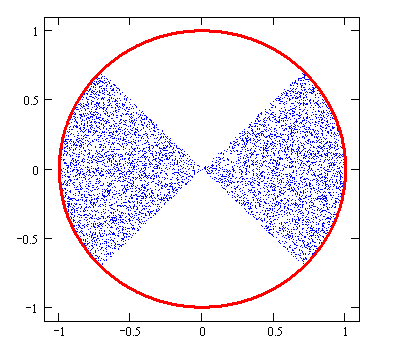
Решением проблемы является переход к неравномерному излучению фотонов при большом расстоянии между исследуемой системой и внешним источником излучения. В этом случае фотоны излучаются исключительно в направлении системы. Вид распределения имеет вид конуса с осью, соединяющей источник и геометрический центр модели. Угол раскрыва конуса соответствует угловому размеру системы, видимой из источника излучения. Вид распределения показан на Рис. 2.7 и Рис. 2.8.
Рис. 2.7. Точки с неравномерным распределением по кругу для внешнего источника излучения |
Рис. 2.8. Неравномерное распределение точек на полусфере для внешнего источника излучения |
Если в случае использования равномерного распределения вес каждого фотона принимается равным единице, то при использовании неравномерного распределения вес каждого фотона необходимо брать равным отношению площади проекции основания конуса на сферу к площади сферы. То есть, при поглощении фотона, излученного с равномерным распределением, счетчик поглощенных фотонов увеличивается на единицу, в то время как при поглощении фотона с неравномерным распределением счетчик увеличивается на отношение площади проекции основания конуса на сферу к площади сферы. Изменение веса при использовании неравномерного распределения необходимо для учета доли фотонов, гарантированно не облучающих систему.
В большинстве случаев число фотонов, излучаемых поверхностью или источником за единицу времени, чрезмерно велико для того, чтобы моделировать испускание, распространение и поглощение отдельного фотона. Поэтому реальный поток излучения заменяют группами фотонов, пучками, имеющими одно и тоже направление распространения и одинаковую длину волны. Приведенный в данном разделе метод расчета распределения частот фотонов и направления их распространения пригоден и для пучков фотонов. Очевидно, что при увеличении количества пучков, их распределение по частотам и направлениям излучения приближается к теоретическому.
В настоящей работе принимается равномерное распределение направления излучения пучков, испускаемых поверхностями элементов, соответствующее Рис. 2.3 и Рис. 2.4. Для точечных источников излучения вид распределения выбирается автоматически в зависимости от расстояния между источником и исследуемой системой. При необходимости учета более сложного распределения описанный метод может быть легко модифицирован.
Плотности
тепловых потоков
и
,
исходящие с граней элементов, в выражении
(2.4) равны величинам, рассчитываемым по
формулам (2.6) и (2.9). Количество пучков,
излучаемое элементами и источниками
излучения на одном шаге времени задается
в явном виде и обозначается
и
соответственно.
После того как определены частоты излучения пучков и направление их испускания, необходимо перейти к расчету хода излучения и его поглощения в элементах исследуемой системы.