2. Практическая часть

Постановка задачи

Исследовать на минимум функцию Розенброка

на области D. Точность по координатам и по значению функции одинаковы: ε=0.001. X_нач= ( –0.5, 0.5)

Методы Ньютона и сопряженных направлений. D – прямоугольник с диагональ­ными вершинами (-1,0) и (1,1).

Функция Розенброка имеет вид

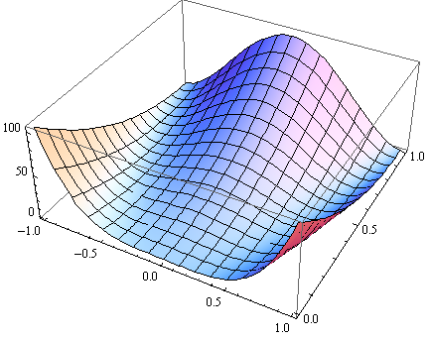
Минимизация методом Ньютона:

Точка минимума с помощью метода Ньютона: (1,1), значение функции . Данное значение достигается за 4 итераций.

Точки минимизации функции методом Ньютона изображены на графике 4.2.

Метод сопряженных направлений.

К методам сопряженных направлений относится метод сопряженных градиентов.

Точка минимума с помощью метода сопряженных градиентов: (1,1), значение функции . Данное значение достигается за 98 итераций.

……

На графику 4.4 представлены направления минимизации к точке (1,1) методом сопряженных градиентов.

ДОДАТОК А