2.3. Метод сопряженных градиентов

Вновь рассмотрим задачу минимизации на квадратичной функции 3.1 с помощью метода 3.2. Попытаемся решить систему взаимносопряженных направлений по правилу

. (2.21)

Из условия сопряженности векторов и имеем

, (2.22)

откуда

. (2.23)

Обоснование того факта, что метод 2.2, 2.12, 2.13 относится к методу сопряженных направлений, содержится в двух следующих леммах.

Лемма 3.3 Векторы иортогональны,

Доказательство. В силу 3.2 имеем , откуда с учетом равенстваполучаем

, (2.24)

И после подстановки значения имеем

. (2.25)

Следовательно,

. (2.26)

Заметим, теперь, что поскольку – точка минимума функциина прямой, то. Поэтому

. (2.27)

Кроме того, равенство 3.13 обеспечивает сопряженность векторов и, откуда следует, что

. (2.28)

В силу 2.16, 2.17 правая часть 2.15 обращается в нуль, т. е.

Лемма 2.4 Пусть , точкии векторыполучены по формулам 2.2, 2.12, 2.13 ивзаимно ортогональны.

Доказательство. Ортогональность и следует из леммы 2.3;по условию,, так как в противном случае, что невозможно из-за ортогональностии; наконец, сопряженность и следует из 2.13.

Предположим, что , векторы взаимно сопряжены, а градиенты взаимно ортогональны.

Тогда по лемме 2.3. При имеем

(2.29)

где первое равенство справедливо в силу 2.14, второе и четвертое – в силу индуктивного предположения, а третье – в силу 2.12. Тем самым доказана взаимная ортогональность векторов .

Далее , иначе из 2.12 следовало бы, что векторылинейно зависимы, что противоречит их взаимной ортогональности. Докажем, чтовзаимно сопряжены.

Действительно , в силу 2.13. По формулам 2.12

, (2.30)

и потому . Следовательно по формуле 2.14

. (2.31)

При

, (2.32)

Где первое равенство справедливо в силу 2.12, второе – в силу индукционного предположения, третье – в силу 2.18, последнее – в силу уже доказаного. Δ

Итак, рассматриваемый метод относится к числу методов сопряженных направлений. Поэтому их следствия теоремы 2.1 следует справедливость следуещего утверждения.

Теорема 2.3. Метод 2.2, 2.12, 2.13 обеспечивает отыскание точки минимума квадратичной функции 2.1 не более чем за шагов.

Замутим, что если окажется, что 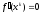при , то вычисления следует прекратить – задача решена. В противном случае формула 2.16 показывает, что, т. е.является направлением убывания. Поэтому при минимизации данной функции 2.1 операции взятия минимума по всей прямой в 2.2 можно заменить операцией взятия минимума по неотрицательной полупрямой. Для получающегося метода

_(2.33)

теорема 2.3 остается справедливой (направления по-прежнему определяются формулами 2.12, 2.13).

До сих пор мы предполагали, что симметрическая матрица А в 2.1 полжительно определена. Однако на практике часто встречаются задачи в которых предполагается, что при всех, т. е. симметрическая матрица А неотрицательно определена.

Теорема 2.4. Если квадратическая функция 2.1 с неотрицательно определенной матрицей А достигает своего минимального значения на , то метод 2.2,2.12, 2.13, обеспечивает отыскания точки минимума, не более, чем зашагов. Если минимальное значение не достигается, то метод позволяет установить этот факт также не более, чем зашагов.