2. Методы сопряженных направлений.

2.1. Методы сопряженных направлений. Их свойства и понятия.

Высокая скорость сходимости метода Ньютона обусловлена тем, что он минимизирует квадратичную функцию

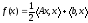, (2.1)

Где А – симметрическая положительно определенная матрица размера nxn , за один шаг. Квазиньютоновские методы позволяют найти минимум квадратичной функции за шагов. На стремлении минимизировать квадратичную функцию за конечно число шагов основана идея метода сопряженных направлений. Точнее говоря, в методах сопряженных направлений требуется найти направлениятакие, что последовательностьодномерных минимизаций вдоль этих направлений приводит к отысканию минимума функции 2.1, т. е.при любом, где

(2.2)

Оказывается, что указаным свойством обладает система взаимно сопряженных относительно матрицы А направлений

Пусть А – симетрическая положительно определенная матрица размера .

Определение 2.1. Векторы (направления) иназываются сопряженными (относительно матрицы А), если они отличны от нуля и. Векторы (направления)называются взаимно сопряженными (относительно матрицы А), если все они отличны от нуля и. (2.3)

Лемма 3.1. Пусть векторы являются взаимно сопряженными. Тогда они линейно независимы.

Доказательство. Пусть это неверно, т. е. при некотором. Тогда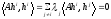, что возможно только при, так как матрица А положительно определена. Полученное противоречие доказывает лемму.

Рассмотрим задачу минимизации на Rⁿ функции 2.1. Будем решать ее методом 2.2. Если векторы , взаимно сопряжены, то метод 3.2 можно назвать методом сопряженных направлений. Однако обычно это название употребляется лишь для тех методов, в которых именно стремление добится условия взаимной сопряженности определяет выбор направлений. К выполнению того же самого условия может привести и реализация совершенно новой идеи.

Теорема 3.1. Если векторы h^k в методе 2.2 взаимно сопряжены, k=0,1,…,m-1, то для функции f, заданой формулой 2.1,

, (2.4)

где – линейное подпространство, натянутое на указанные векторы.

Доказательство. С учетом 2.2 и определения 2.1 имеем

(2.5)

Используя это равенство, получаем

(2.6)

Отсюда

Δ (2.7)

Следствие. Если векторы h^k в методе 2.2 взаимно сопряженны, k=0,1,…,n-1, то для функции f, заданной формулой 2.1, и произвольной точки

. (2.8)

Таким образом, метод 2.2 позволяет найти точку минимума квадратичной функции 2.1 не более чем за n шагов.

2.2. Метод сопряженных направлений нулевого порядка.

Алгоритм состоит из последовательности циклов, k-й из которых определяется начальной точкой t⁰(k) и направлениями минимизации p⁰(k), p¹(k), …, p^n-1(k). На нулевом цикле в качестве t⁰(0), выбирается произвольная точка , в качествеp⁰(0), p¹(k), …, p^n-1(k) – направления координатных осей.

Очередной k-й цикл состоит в последовательном решении одномерных задач

_(2.9)

Тем самым определяется шаг из точки в точку

,(2.10)

где итаковы, что

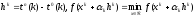. (2.11)

После завершения k-го цикланачальная точка и направления минимизации (k+1)-го цикла определяются по формулам

. (2.12)

Критерием остановки может служить выполнение неравенства , где– заранее выбраное малое положительное число.

Теорема 3.2. Если векторы в методе 2.5-2.7 отличны от нуля, то для функцииf, заданой формулой 2.1

. (2.13)

Доказательство. Учитывая следствие из теоремы 3.1, достаточно показать, что векторы 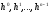взаимно сопряжены. Пусть. Предположив, что векторывзаимно сопряжены, докажем, что векторсопряжен с векторами.

Заметим, что и, стало быть, точкаtⁿ(k), согласно формулам 2.5, получена из точки t^n-k(k) с помощью последовательности одномерных минимизаций вдоль направлений . Это, в силу теоремы 2.1, означает, что

. (2.14)

Аналогично, точка t⁰(k) получена из точки t^n-k+1(k) помощью последовательности одномерных минимизаций вдоль тех же направлений, и поэтому

_(2.15)

Доказываемое утверждение теперь непосредственно следует с леммы 2.2 так как .

Предположение теоремы 2.2 о том, что отличны от нуля, выполняется далеко не всегда. Система векторовможет при некоторомk оказатся линейно зависимой (или «почти» линейно зависимой), в результате чего метод может не обеспечить отыскание минимума даже квадратичной функции.

Опишем модификацию метода 2.5-2.7, приводящую к эффективному алгоритму минимизации.

После завершения k-го цикла проверяется выполнение неравенств . Если хотя бы одно с них выполнено, то производится остановка. В противном случае проверяется выполнение неравенства

, (2.16)

где

. (2.17)

Если оно выполнено, то направления минимизации (k+1)-го цикла остаются прежними, т. е.

. (2.18)

Если нет, то направления минимизации (k+1)-го цикла определяется по формулам

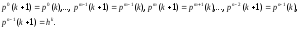(2.19)

В обоих случаях начальная точка (k+1)-го цикла вычисляется так, же как и в исходном алгоритме:

_(2.20)