1. Метод Ньютона и его модификации

1.1. Метод Ньютона

Предположим, функция f выпукла и дважды дифференцируема на Rⁿ, причем матрица f’’(x) невырождена на Rⁿ. В методе Ньютона последовательность x⁰, x¹, x²,… генерируется исходя из следующих соображений.

По определению дважды дифференцируемой функции для очередной точки x^k имеем

. (1.1)

Для определения следующей точки x^k+1 минимизируется функция f_k(x), является квадратичной частью приращения f(x)-f(x^k), т.е. решается задача

. (1.2)

Ясно, что f_k’’(x)=f’’(x^k) . Так как необходимым и достаточным условием выпуклости функции является неотрицательная определенность матрицы ее вторых производных, а функция f выпукла по условию, то функция f_k выпукла. Поэтому необходимое и достаточное условие имеет вид

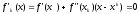. (1.3)

Решая полученную систему линейных уравнений и принимая найденную точку минимума за x^k+1, получаем

. (1.4)

Данное соотношение определяет метод Ньютона минимизации функции f, совпадающий, как нетрудно увидеть методом Ньютона для решения системы уравнений f’(x)=0.

Исследуем сходимость метода.

1.2. Сходимость метода Ньютона и оценка скорости сходимости

Теорема. Пусть функция f дважды дифференцируема, сильно выпукла с константой θ>0 на Rⁿ и удовлетворяет условию

, (1.5)

где М>0, а начальная точка x⁰ такова, что , т.е.

. (1.6)

Тогда последовательность 1.1 сходится к точке минимума х* с квадратичной скоростью:

. (1.7)

Доказательство. Точка минимума х* существует и единственна. Условие сильной выпуклости эквивалентно следующему:

. (1.8)

Отсюда следует, что матрица f’’(x) положительно определенна и потому невырождена при всех xRⁿ . Таким образом, метод 1.1 определен корректно.

Учитывая, что f’(x*)=0, получаем

, (1.9)

т.е.

. (1.10)

Оценим величину Интегрируя поt от 0 до 1 соотношение

. (1.11)

И вычитая с обеих частей полученного равенства , имеем

, (1.12)

Откуда, в силу 1.2 имеем

. (1.13)

Подставляя сюда , приходим к неравенству

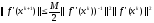. (1.14)

Оценим теперь величину . Полагаяполучаем из 1.4

_(1.15)

откуда

. (1.16)

С учетом полученной оценки из 1.6 следует, что

. (1.17)

Это неравенство справедливо при всех х поэтому, используя 1.3, получаем

. (1.18)

Утверждение теоремы теперь непосредственно следует из 1.5.

Таким образом, сходимость метода Ньютона доказана лишь дл достаточно хорошего начального приближения х⁰. При этом условие 1.3, гарантирующее сходимость для данного приближения, труднопроверяемо, так как фигурирующие в нем константы, как правило, неизвестны.

Сложность отыскания нужного начального приближения является недостатком метода Ньютона. Еще более существенным недостатком является трудоемкость метода, обусловленная необходимостью вычисления и обращения на каждом шаге матрицы вторых производных минимизируемой функции.

В силу названных причин применение классического метода Ньютона далеко не всегда приводит к успеху. Многочисленные модификации направлены на то, чтобы, сохраняя основное достоинство метода Ньютона – его быструю сходимость, уменьшить трудоемкость и ослабить требования на выбор начального приближения.