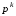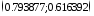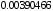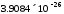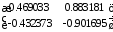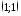2. Практическая часть

1. Содержательная и формальная постановка задачи.

Рассмотрим функцию Розенброка для двух переменных вида:

(2.1)

Она имеет глобальный минимум в точке где

Необходимо исследовать на минимум функцию Розенброка на области с точностью по координатами с начальным приближением. Областьвсе пространство.

2. Результаты вычислительного эксперимента.

Рис. 2.1 – График функции Розенброка

Рис. 2.2 – Графические итерации к методу сопряженных направлений 0-го порядка

Рис. 2.3 – Графические итерации к методу сопряженных направлений Пауэлла

3. Сравнительный анализ методов.Результаты вычислений методов приведены в таблицах 2.1, 2.2 и 2.3.

Таблица 2.1 – Результаты сравнения работы методов

Название метода	Количество итераций	Время работы
Метод сопряженных направлений 0-го порядка	7	1.4940854
Метод сопряженных направлений Пауэлла	7	2.0441169

Таблица 2.2 – Результаты вычислений методом сопряженных направлений 0-го порядка
№ итерации		X
0
1
2
3
4
5
6
7
Таблица 2.3 – Результаты вычислений методом сопряженных направлений Пауэлла
№ итерации		X
0
1
2
3
4
5
6
7

Проводя сравнительный анализ рассмотренных методов, можно сказать, что все они позволили найти решение поставленной задачи. Как видно по таблице, оба метода сошлись за равное количество итераций, но работу метода сопряженных направлений 0-го порядка потребовалось меньше времени.

Основываясь на результатах данной работы, можно сказать, что для решения задач, подобных поставленной, на практике применимы оба метода, т. к. метод сопряженных направлений 0-го порядка затратил меньше времени, а метод Пауэлла получил более точное решение при не большой разнице во времени.

Заключение

В результате выполнения данной курсовой работы, я рассмотрел методы сопряженных направлений 0-го порядка и Пауэлла. На основе этих методов я исследовал на минимум функцию Розенброка. Проводя сравнительный анализ рассмотренных методов, можно сказать, что все они позволили найти решение поставленной задачи и их можно использовать для решения подобных задач.

Метод сопряженных направлений разработан для решения задач, в которых целевая функция является квадратичной. Метод поиска интересен тем, что имеет высокую скорость сходимости в задачах с квадратичной целевой функцией и малым количеством параметров — всего n итераций. Однако, если функция не является квадратичной, то количество итераций увеличивается.

До полного завершения курсовой работы, мною была написана программа к методам.

Перечень использованных источников

1. Кузнецов Ю.Н., Кузубов В. И., Волощенко А. Б., Математическое программирование.

2. Сухарев А.Г. Курс методов оптимизации / Сухарев А.Г., Тимохов А.В., Федоров В.В. – М.: Наука, 2005. – 368 с.

3. Реклейтис Г., Рейвиндран А., Рэгсдел К. Оптимизация в технике. Книга 1. – М.:Мир, 1986. – 347 с.