
- •Пояснительная записка
- •Реферат
- •Содержание
- •Введение
- •Теоретическая часть
- •Понятие сопряженных направлений и их свойства. Пусть а – симетрическая положительно определенная матрица размера.
- •Практическая часть
- •Содержательная и формальная постановка задачи.
- •Результаты вычислительного эксперимента.
- •Сравнительный анализ методов.Результаты вычислений методов приведены в таблицах 2.1, 2.2 и 2.3.
- •Заключение
- •Перечень использованных источников
- •Приложение а
Понятие сопряженных направлений и их свойства. Пусть а – симетрическая положительно определенная матрица размера.
Определение 1.1.
Векторы (направления)
 и
и называются сопряженными (относительно
матрицы А), если они отличны от нуля и
называются сопряженными (относительно
матрицы А), если они отличны от нуля и .
Векторы (направления)
.
Векторы (направления) называются взаимно сопряженными
(относительно матрицы А), если все они
отличны от нуля и
называются взаимно сопряженными
(относительно матрицы А), если все они
отличны от нуля и .
.
Лемма 1.1. Пусть
векторы
 являются взаимно сопряженными. Тогда
они линейно независимы.
являются взаимно сопряженными. Тогда
они линейно независимы.
Доказательство.
Пусть это неверно, т. е.
 при некотором
при некотором
 .
Тогда
.
Тогда ,
что возможно только при
,
что возможно только при
 ,
так как матрица А положительно определена.
Полученное противоречие доказывает
лемму.
,
так как матрица А положительно определена.
Полученное противоречие доказывает
лемму.
Рассмотрим задачу
минимизации на Rnфункции12. Будем решать
ее методом 13. Если векторы ,
взаимно сопряжены, то метод 13 можно
назвать методом сопряженных направлений.
Однако обычно это название употребляется
лишь для тех методов, в которых именно
стремление добится условия взаимной
сопряженности определяет выбор
направлений
,
взаимно сопряжены, то метод 13 можно
назвать методом сопряженных направлений.
Однако обычно это название употребляется
лишь для тех методов, в которых именно
стремление добится условия взаимной
сопряженности определяет выбор
направлений .
К выполнению того же самого условия
может привести и реализация совершенно
иной идеи.
.
К выполнению того же самого условия
может привести и реализация совершенно
иной идеи.
Теорема 1.1. Если
векторы
 в методе 13 взаимно сопряжены,k=0,1,…,m-1,
то для функцииf,
заданой формулой 12,
в методе 13 взаимно сопряжены,k=0,1,…,m-1,
то для функцииf,
заданой формулой 12,
 ,
,
где
 – линейное подпространство, натянутое
на указанные векторы.
– линейное подпространство, натянутое
на указанные векторы.
Доказательство. С учетом 2.2 и определения 2.1 имеем
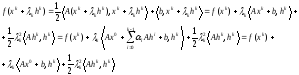
Используя это равенство, получаем
 Отсюда
Отсюда
 Δ
Δ
Следствие. Если
векторы
 в методе 13 взаимно сопряженны,k=0,1,…,n-1,
то для функцииf,
заданной формулой 2.1, и произвольной
точки
в методе 13 взаимно сопряженны,k=0,1,…,n-1,
то для функцииf,
заданной формулой 2.1, и произвольной
точки

Таким образом,
метод 13 позволяет найти точку минимума
квадратичной функции 12 не более чем
за
 шагов.
шагов.
Метод сопряженных направлений нулевого порядка.Алгоритм состоит из последовательности циклов,
 -й
из которых определяется начальной
точкой
-й
из которых определяется начальной
точкой и направлениями минимизации
и направлениями минимизации ,
, .
На нулевом цикле в качестве
.
На нулевом цикле в качестве выбирается произвольная точка
выбирается произвольная точка ,
в качестве
,
в качестве - направления координатных осей.
- направления координатных осей.
Очередной
 -й
цикл состоит в последовательном решении
одномерных задач
-й
цикл состоит в последовательном решении
одномерных задач
 414\* MERGEFORMAT (.)
414\* MERGEFORMAT (.)
Тем самым определяется
шаг из точки
 в точку
в точку
 ,
515\* MERGEFORMAT (.)
,
515\* MERGEFORMAT (.)
где
 и
и таковы, что
таковы, что
 .
.
После завершения
 -го
цикла начальная точка и направления
минимизации
-го
цикла начальная точка и направления
минимизации -го
цикла определяются по формулам
-го
цикла определяются по формулам
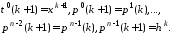 616\* MERGEFORMAT (.)
616\* MERGEFORMAT (.)
Критерием остановки
может служить выполнение неравенства
 ,
где
,
где - заранее выбранное малое положительное
число.
- заранее выбранное малое положительное
число.
Теорема 1.2. Если
векторы
 в методе 14-16 отличны от нуля, то для
функции
в методе 14-16 отличны от нуля, то для
функции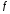 ,
заданной формулой 12,
,
заданной формулой 12, .
.
Предположение
теоремы 1.2 о том, что
 отличны от нуля выполняется далеко не
всегда. Система векторов
отличны от нуля выполняется далеко не
всегда. Система векторов может при некотором
может при некотором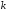 оказаться линейно зависимой, в результате
чего метод может не обеспечить отыскание
минимума даже квадратичной функции.
оказаться линейно зависимой, в результате
чего метод может не обеспечить отыскание
минимума даже квадратичной функции.
Опишем модификацию метода 14-16, приводящую к эффективному алгоритму минимизации.
После завершения
 -го
цикла проверяется выполнение неравенств
-го
цикла проверяется выполнение неравенств .
Если хотя бы одно из них выполнено, то
производится остановка. В противном
случае проверяется выполнение неравенства
.
Если хотя бы одно из них выполнено, то
производится остановка. В противном
случае проверяется выполнение неравенства
 717\* MERGEFORMAT (.)
717\* MERGEFORMAT (.)
где

Если оно выполнено,
то направления минимизации
 -го
цикла остаются прежними, т.е.
-го
цикла остаются прежними, т.е.
 818\* MERGEFORMAT (.)
818\* MERGEFORMAT (.)
Если нет, то
направления минимизации
 -го
цикла определяются по формулам
-го
цикла определяются по формулам
 919\* MERGEFORMAT (.)
919\* MERGEFORMAT (.)
В обоих случаях
начальная точка
 -го
цикла вычисляется так же, как и в исходном
алгоритме:
-го
цикла вычисляется так же, как и в исходном
алгоритме:
 10110\* MERGEFORMAT (.)
10110\* MERGEFORMAT (.)
Можно сказать, что
модифицированный алгоритм 14, 15,17-110ни
при каком не приводит при минимизации квадратичной
функции к линейно зависимой системе
направлений
не приводит при минимизации квадратичной
функции к линейно зависимой системе
направлений .
С увеличением
.
С увеличением для этой системы во все возрастающей
степени выполняется свойство
«приблизительной» взаимной сопряженности
(при этом, однако, отыскание минимума
квадратичной функции за
для этой системы во все возрастающей
степени выполняется свойство
«приблизительной» взаимной сопряженности
(при этом, однако, отыскание минимума
квадратичной функции за циклов не гарантируется). Алгоритм 14,15,17-110применяется для минимизации выпуклых
гладких функций (не обязательно
квадратичных). Упомянутые свойства
обеспечивают на практике его сравнительно
высокую эффективность.
циклов не гарантируется). Алгоритм 14,15,17-110применяется для минимизации выпуклых
гладких функций (не обязательно
квадратичных). Упомянутые свойства
обеспечивают на практике его сравнительно
высокую эффективность.
Метод сопряженныхнаправлений Пауэлла. Наиболее эффективным из алгоритмов прямого поиска является метод, разработанный Пауэллом, в особенности его модифицированные варианты, предложенные Зангвиллом и Брентом. При работе этого алгоритма информация, полученная на предыдущих итерациях, используется для построения векторов направлений поиска, а также для устранения зацикливания последовательности координатных поисков. Метод ориентирован на решение задач с квадратичными целевыми функциями и основывается на фундаментальных теоретических результатах.
Задачи с квадратичными целевыми функциями занимают важное место в теории оптимизации по двум причинам.
1. Квадратичная функция представляет простейший тип нелинейных функций, для которых может быть сформулирована задача безусловной оптимизации (линейные функции не обладают внутренними оптимумами). Следовательно, если с помощью того или иного метода успешно решаются задачи оптимизации с целевыми функциями общего вида, то такой метод должен оказаться эффективным при решении задач с квадратичными функциями.
2. В окрестности точки оптимума любую нелинейную функцию можно аппроксимировать квадратичной функцией (поскольку линейный член разложения Тейлора обращается в нуль). Следовательно, работа алгоритма при решении задач с квадратичными функциями позволяет получить определенное представление о сходимости алгоритма в случае, когда минимизируется функция общего вида.
Основная идея
алгоритма заключается в том, что если
квадратичная функция
 переменных приведена к виду суммы
полных квадратов, то ее оптимум может
быть найден в результате реализации
переменных приведена к виду суммы
полных квадратов, то ее оптимум может
быть найден в результате реализации одномерных
поисков по преобразованным координатным
направлениям.
одномерных
поисков по преобразованным координатным
направлениям.
Процедура преобразования квадратичной функции
 11111\* MERGEFORMAT (.)
11111\* MERGEFORMAT (.)
к виду суммы полных квадратов эквивалентна нахождению такой матрицы преобразования Т, которая приводит матрицу квадратичной формы к диагональному виду. Таким образом, заданная квадратичная форма
 12112\* MERGEFORMAT (.)
12112\* MERGEFORMAT (.)
путем преобразования
 13113\* MERGEFORMAT (.)
13113\* MERGEFORMAT (.)
Приводится к виду
 14114\* MERGEFORMAT (.)
14114\* MERGEFORMAT (.)
где D– диагональная матрица, т.е. элементыDотличны от нуля только
при .
.
Пусть
 -
- -й столбец матрицы Т. Тогда преобразование
113 позволяет записать каждый вектор
-й столбец матрицы Т. Тогда преобразование
113 позволяет записать каждый вектор в
виде линейной комбинации вектор-столбцов
в
виде линейной комбинации вектор-столбцов :
:
 15115\* MERGEFORMAT (.)
15115\* MERGEFORMAT (.)
Другими словами,
вместо координат вектора
 в стандартной координатной системе,
определяемой множеством векторов
в стандартной координатной системе,
определяемой множеством векторов ,
используются координаты вектора в новой
координатной системе, заданной векторами
,
используются координаты вектора в новой
координатной системе, заданной векторами .
Кроме того, система векторов
.
Кроме того, система векторов соответствует главным осям рассматриваемой
квадратичной формы, поскольку матрица
квадратичной формы приводится к
диагональному виду. Такая ситуация
возникает если квадратичную функцию с
перекрестными членами, линии уровня
записать в новой координатной системе,
оси которой совпадают с большой и малой
осями квадратичной функции.
соответствует главным осям рассматриваемой
квадратичной формы, поскольку матрица
квадратичной формы приводится к
диагональному виду. Такая ситуация
возникает если квадратичную функцию с
перекрестными членами, линии уровня
записать в новой координатной системе,
оси которой совпадают с большой и малой
осями квадратичной функции.
Итак, с помощью
преобразования переменных квадратичной
функции строится новая система координат,
совпадающих с главными осями квадратичной
функции. Следовательно, одномерный
поиск точки оптимума в пространстве
преобразованных переменных
 эквивалентен поиску вдоль каждой из
главных осей определяются векторами
эквивалентен поиску вдоль каждой из
главных осей определяются векторами ,
одномерный поиск проводится в направлениях,
заданных этими векторами.
,
одномерный поиск проводится в направлениях,
заданных этими векторами.
Если система
векторов
 или система сопряженных направлений,
построена, то точку оптимума квадратичной
функции можно найти в результате
реализации в точности
или система сопряженных направлений,
построена, то точку оптимума квадратичной
функции можно найти в результате
реализации в точности одномерных поисков, которые проводятся
вдоль каждого из
одномерных поисков, которые проводятся
вдоль каждого из направлений
направлений
 .
Таким образом, нерешенными остаются
лишь вопросы, связанные с построением
системы векторов
.
Таким образом, нерешенными остаются
лишь вопросы, связанные с построением
системы векторов .
Если матрица
.
Если матрица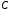 известна, то матрицу преобразования
известна, то матрицу преобразования можно найти с помощью метода Гаусса —
Жордана. Метод Гаусса — Жордана позволяет
представить матрицу
можно найти с помощью метода Гаусса —
Жордана. Метод Гаусса — Жордана позволяет
представить матрицу в виде произведения
в виде произведения
 ,
откуда 16116\* MERGEFORMAT (.)
,
откуда 16116\* MERGEFORMAT (.)
 17117\* MERGEFORMAT (.)
17117\* MERGEFORMAT (.)
Однако матрица
 (или ее оценка) в данном случае неизвестна,
поскольку речь идет о построении метода
решения задач безусловной оптимизации
с целевой функцией
(или ее оценка) в данном случае неизвестна,
поскольку речь идет о построении метода
решения задач безусловной оптимизации
с целевой функцией ,
при реализации которого используются
только значения функции и не используются
значения первых и тем более вторых
производных. Тем не менее и в этом случае
можно определить систему сопряженных
направлений на основе следующего
элементарного свойства квадратичных
функций.
,
при реализации которого используются
только значения функции и не используются
значения первых и тем более вторых
производных. Тем не менее и в этом случае
можно определить систему сопряженных
направлений на основе следующего
элементарного свойства квадратичных
функций.
Свойство параллельного
подпространства. Пусть заданы квадратичная
функция
 ,
две произвольные несовпадающие точки
,
две произвольные несовпадающие точки и
и ,
а также направление
,
а также направление .
Если точка
.
Если точка минимизирует
минимизирует ,
а точка
,
а точка минимизирует
минимизирует ,
то направление
,
то направление сопряжено с
сопряжено с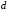
Докажем теорему
о свойстве параллельного подпространства.
По определению
 - сопряженные направления задаются
системой вектор-столбцов матрицы
- сопряженные направления задаются
системой вектор-столбцов матрицы ,
которая приводит матрицу
,
которая приводит матрицу к диагональному виду:
к диагональному виду:
 18118\* MERGEFORMAT (.)
18118\* MERGEFORMAT (.)
Поскольку все
внедиагональные элементы
 равны нулю, отсюда следует, что
равны нулю, отсюда следует, что
 19119\* MERGEFORMAT (.)
19119\* MERGEFORMAT (.)
Где
 -
- -й
столбец матрицы
-й
столбец матрицы .
Таким образом, мы получили возможность
дать более удобное, эквивалентное и,
по-видимому, более конструктивное
определение сопряженности направлений.
.
Таким образом, мы получили возможность
дать более удобное, эквивалентное и,
по-видимому, более конструктивное
определение сопряженности направлений.
Сопряженные
направления. Пусть С — симметрическая
матрица порядка
 направления
направления ,
называются С-сопряженными, если эти
направления линейно независимы и
,
называются С-сопряженными, если эти
направления линейно независимы и
 — о для всех
— о для всех 20120\* MERGEFORMAT (.)
20120\* MERGEFORMAT (.)
Опять обратимся к квадратичной функции общего вида

Точки прямой,
исходящей из
 в направленииd,
задаются формулой
в направленииd,
задаются формулой
 .
.
Минимум
 вдоль направленияd
определяется путем нахождения значения
вдоль направленияd
определяется путем нахождения значения ,
при котором
,
при котором .
Вычислим эту производную по правилу
дифференцирования сложной функции:
.
Вычислим эту производную по правилу
дифференцирования сложной функции:
 21121\* MERGEFORMAT (.)
21121\* MERGEFORMAT (.)
По предположению
теоремы минимум достигается в точке
 ,
следовательно,
,
следовательно,
 22122\* MERGEFORMAT (.)
22122\* MERGEFORMAT (.)
Аналогично, так
как минимум
 при движении из точки
при движении из точки в направленииd
достигается
в направленииd
достигается в точке имеем
в точке имеем
 23123\* MERGEFORMAT (.)
23123\* MERGEFORMAT (.)
Вычитая 122из123, получаем
 24124\* MERGEFORMAT (.)
24124\* MERGEFORMAT (.)
В соответствии с
данным выше определением направления
 и
и оказываются С-сопряженными, и свойство
параллельного подпространства для
квадратичных функций доказано.
оказываются С-сопряженными, и свойство
параллельного подпространства для
квадратичных функций доказано.
Обобщенный алгоритм метода сопряженных направлений Пауэлла.
Шаг 1. Задать
начальную точку
 и систему
и систему линейно независимых направлений;
возможен случай, когда
линейно независимых направлений;
возможен случай, когда .
.
Шаг 2. Минимизировать
 при последовательном движении по
при последовательном движении по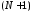 направлениям; при этом полученная ранее
точка минимума берется в качестве
исходной, а направление
направлениям; при этом полученная ранее
точка минимума берется в качестве
исходной, а направление используется как при первом, так и
последнем поиске.
используется как при первом, так и
последнем поиске.
Шаг 3. Определить новое сопряженное направление с помощью обобщенного свойства параллельного подпространства.
Шаг 4. Заменить
 на
на и т. д. Заменить
и т. д. Заменить сопряженным направлением. Перейти к
шагу 2.
сопряженным направлением. Перейти к
шагу 2.
Для того чтобы
применить изложенный метод на практике,
его необходимо дополнить процедурами
проверки сходимости и линейной
независимости системы направлений.
Проверка линейной независимости особенно
важна в тех случаях, когда функция
 не является квадратичной.
не является квадратичной.
Из способа построения
алгоритма следует, что в случае, когда
целевая функция квадратична и обладает
минимумом, точка минимума находится в
результате реализации
 циклов, включающих шаги 2, 3 и 4, где
циклов, включающих шаги 2, 3 и 4, где — количество переменных. Если же
функция не является квадратичной, то
требуется более чем
— количество переменных. Если же
функция не является квадратичной, то
требуется более чем циклов. Вместе с тем можно дать строгое
доказательство того, что при некотором
предположении метод Пауэлла сходится
к точке локального минимума с суперлинейной
скоростью.
циклов. Вместе с тем можно дать строгое
доказательство того, что при некотором
предположении метод Пауэлла сходится
к точке локального минимума с суперлинейной
скоростью.
Скорость сходимости.
Рассматриваемый метод позволяет
построить последовательность точек
 ,
которая сходится к решению
,
которая сходится к решению . Метод называется сходящимся, если
неравенство
. Метод называется сходящимся, если
неравенство
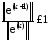 ,
где 25125\* MERGEFORMAT (.)
,
где 25125\* MERGEFORMAT (.)
 ,
26126\* MERGEFORMAT (.)
,
26126\* MERGEFORMAT (.)
выполняется на
каждой итерации. Поскольку при расчетах
обычно оперируют конечными десятичными
дробями, даже самый эффективный алгоритм
требует проведения бесконечной
последовательности итераций. Поэтому
в первую очередь интерес представляют
асимптотические свойства сходимости
изучаемых методов. Будем говорить, что
алгоритм обладает сходимостью порядка
 ,
если
,
если
 27127\* MERGEFORMAT (.)
27127\* MERGEFORMAT (.)
где
 -
постоянная величина. Из формулы 125
следует, что при
-
постоянная величина. Из формулы 125
следует, что при имеет место неравенство
имеет место неравенство .
Если
.
Если или
или ,
то алгоритм характеризуется линейной
или квадратичной скоростью сходимости
соответственно. При
,
то алгоритм характеризуется линейной
или квадратичной скоростью сходимости
соответственно. При и
и алгоритм характеризуется суперлинейной
скоростью сходимости.
алгоритм характеризуется суперлинейной
скоростью сходимости.
