REVIZED / 12_Линейное_программирование

Методы оптимизации: Часть I

12. Линейное программирование

Определение 1. Задачей линейного программирования называется задача выпуклого программирования, у которой все функции являются линейными.

Таким образом, задача линейного программирования является задачей нахождения условного экстремума линейной функции на выпуклом многогранном множестве, образованном системой линейных неравенств. Целью данного параграфа является изучение тех свойств задачи линейного программирования, которые присущи только этому классу задач и, вообще говоря, не имеют места для задач выпуклого программирования.

В предыдущих разделах пособия мы изучали задачи минимизации. Задача линейного программирования чаще формулируется как задача максимизации. Это объясняется тем, что ее истоки связаны с экономическими приложениями, например, с проблемой планирования производства с целью максимизации дохода.

Итак, общая форма записи задачи линейного программирования имеет вид:

при условиях

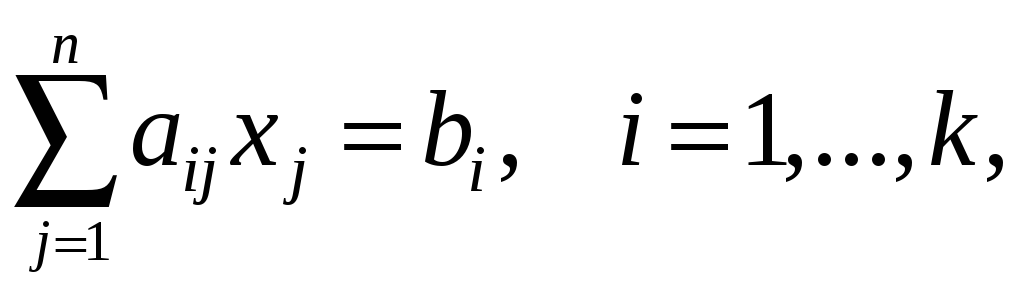
Введем следующие обозначения: ; ; – матрица размерности ; – вектор-строка матрицы , ; – вектор-столбец матрицы , .

В дальнейшем будем использовать следующие две формы записи задачи линейного программирования.

Каноническая форма:

при условиях

Симметричная форма:

при условиях

Задача линейного программирования легко переводится из одной формы записи в другую при помощи простых формальных преобразований.

Легко увидеть, что задача линейного программирования имеет решение, если допустимая область , определяемая системой ограничений,

непуста и целевая функция ограничена сверху на . Если же либо множество пусто, либо функция неограниченна сверху на , то задача линейного программирования не имеет решения.

Все свойства задачи выпуклого программирования, естественно, имеют место и для задачи линейного программирования.

Укажем теперь основное свойство задачи линейного программирования, которое отличает ее от задачи выпуклого программирования.

Теорема 1. Пусть задача линейного программирования в симметричной форме имеет решение. Тогда существует вершина множества , которая является решением задачи.

Доказательство. Пусть вектор – решение задачи. Очевидно, что ранг системы ограничений задачи равен , тогда по теореме 9.6 . Поэтому существуют векторы и такие, что . Отсюда

. (2)

Как следует из теоремы 9.7, . В то же время, так как – условный максимум, вектор не является направлением возрастания функции в точке . Тогда согласно замечанию к теореме 5.2 .

Следовательно, из (2) получаем неравенство . Так как – точка максимума, это неравенство может выполниться лишь как равенство

. (3)

Так как , а (см. теорему 9.6), то , где векторы – все вершины выпуклого многогранного множества . Тогда из (3)

. (4)

Пусть номер вершины множества таков, что . Тогда из равенства (4), учитывая неотрицательность всеx , имеем соотношения . Следовательно, так как вектор – точка максимума, . Что и требовалось.

68