Методы оптимизации: Семестр II

7. Проекция точки на множество

Определение 1. Проекцией точки на множество называется вектор , удовлетворяющий условию

. (1)

Иногда проекцию точки на множество будем обозначать .

Легко увидеть, что тогда и только тогда, когда .

Очевидно также, что имеет место равенство

. (2)

Таким образом, согласно (2) отыскание проекции является задачей минимизации функции на множестве . Заметим при этом, что функция является строго выпуклой (в этом нетрудно убедиться, пользуясь критериями, изученными в параграфе 4).

Существование и единственность проекции зависят от свойств множества . В связи с этим познакомимся со следующими двумя теоремами.

Теорема 1. Пусть – замкнутое множество из _, тогда существует для любого .

Доказательство. Для произвольной точки

обозначим .

Очевидно, что . Поэтому задача (1) эквивалентна задаче

. (3)

Решение задачи (3) существует, так как множество компактно, а функция непрерывна.

Нарушение условия теоремы 1 может привести к отсутствию проекции. Например, проекция не существует, если множество открыто, а вектор не принадлежит множеству .

Теорема 2. Пусть – выпуклое замкнутое множество из _, тогда всякая точка имеет единственную проекцию на множество .

Доказательство. Существование проекции доказано в предыдущей теореме. Докажем ее единственность. Поскольку, как отмечено выше, функция строго выпукла по y, единственность ее минимума на выпуклом множестве вытекает из теоремы 6.3. Что и требовалось.

Нарушение условия выпуклости множества в теореме 2 может привести к неединственности проекции.

Далее приведем критерий, который может быть полезен для нахождения проекции.

Теорема 3. Для того, чтобы точка была проекцией на выпуклое замкнутое множество , необходимо и достаточно, чтобы для всех выполнялось неравенство

. (4)

Доказательство. Для того, чтобы вектор удовлетворял равенству (2), необходимо и достаточно, как следует из теоремы 6.5, чтобы в точке выполнялось неравенство

, (5)

где . Так как , а

, то условия (5) и (4) эквивалентны. Что и требовалось.

Отыскание проекции – это задача минимизации выпуклой функции на выпуклом множестве. Решать такие задачи мы только лишь учимся. Необходимо заметить, что, как правило, отыскать точно проекцию невозможно. Однако при достаточно «простых» множествах проекцию можно вычислить по явным формулам. Приведем несколько примеров таких множеств.

Неотрицательный ортант:

.

Обозначим j-ую координату вектора через . Тогда

.

Гиперпараллелепипед:

.

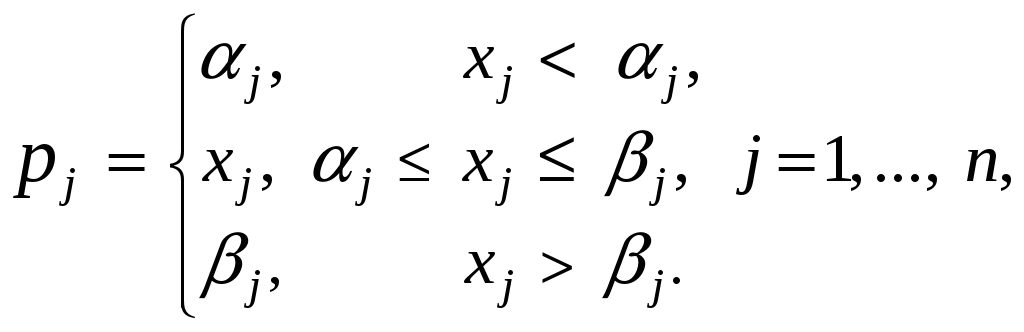
Шар:

.

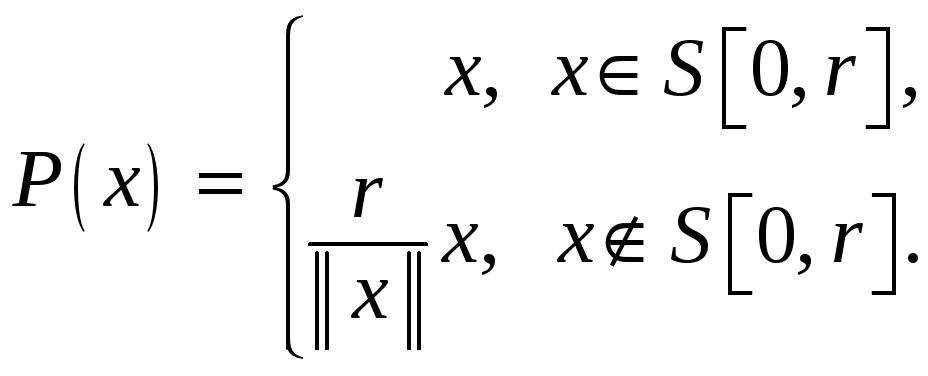
Гиперплоскость:

,

где

.

Полупространство:

.

Многообразие:

,

где – матрица размерности , .

В тех же случаях, когда множество является более «сложным», проекцию находят приближенно с помощью итерационных процедур.

44