Методы оптимизации: Часть I

6. экстремальные свойства выпуклых функций

Данный параграф посвящен изучению экстремумов выпуклых функций на выпуклых множествах. Из теорем, с которыми мы здесь познакомимся, следует, что этот класс задач на экстремум удобен для исследования и решения.

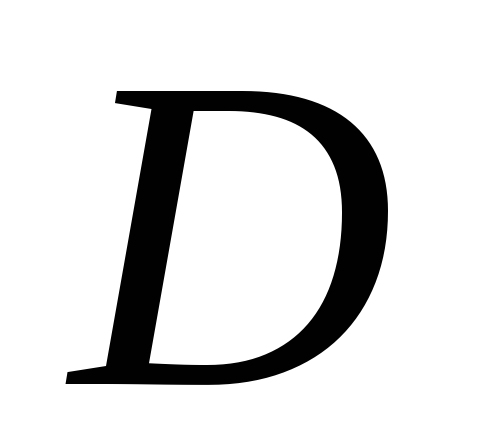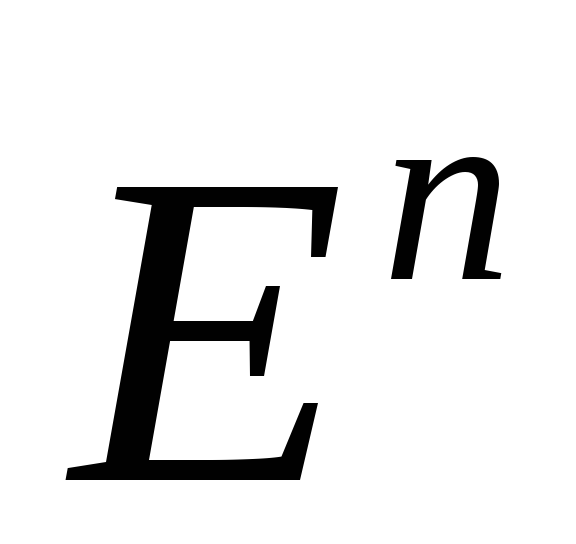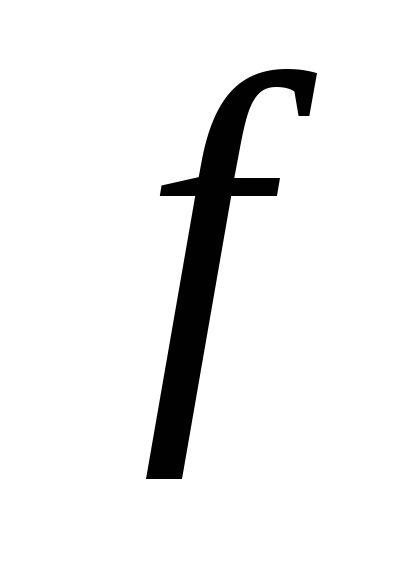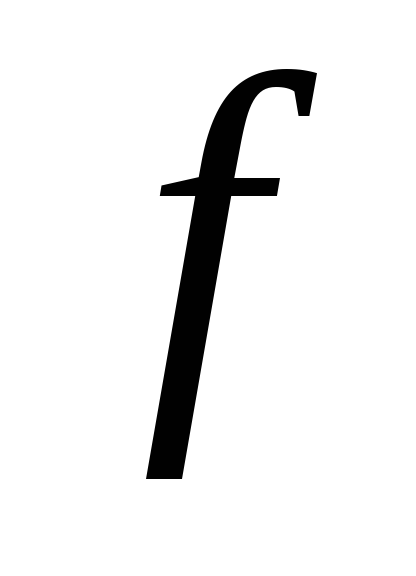Теорема 1. Пусть – выпуклое множество из , функция – выпукла на . Тогда всякий локальный условный минимум функции на множестве является и глобальным.

Доказательство. Пусть – точка локального минимума функции 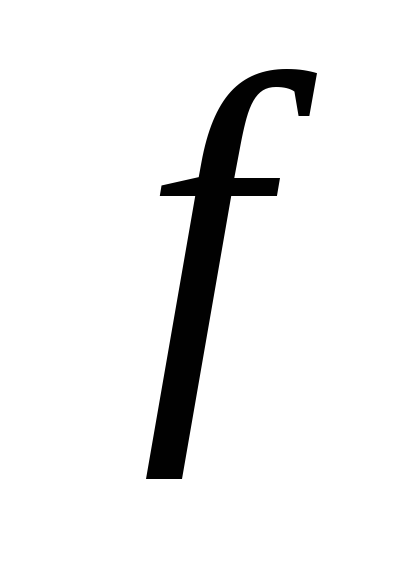на множестве 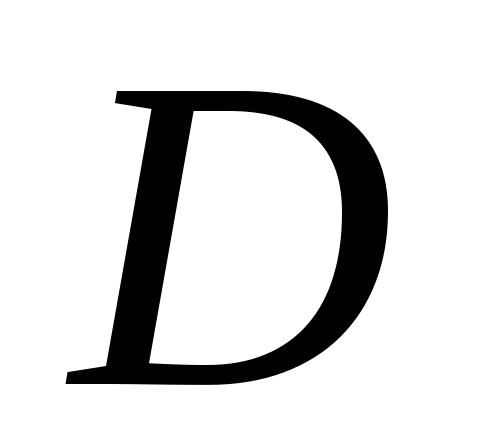. Тогда существует такое число , что для всех 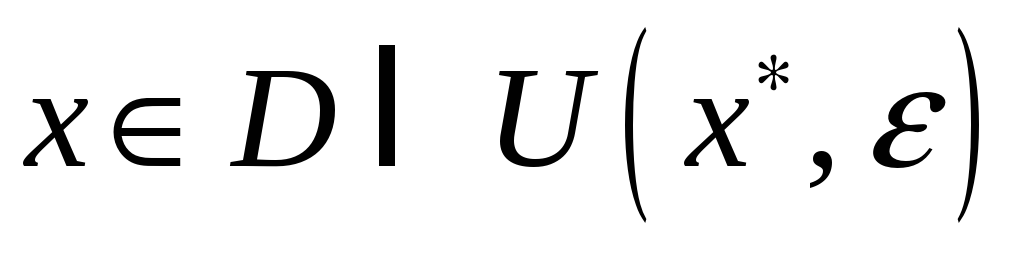выполняется неравенство

. (1)

(Здесь 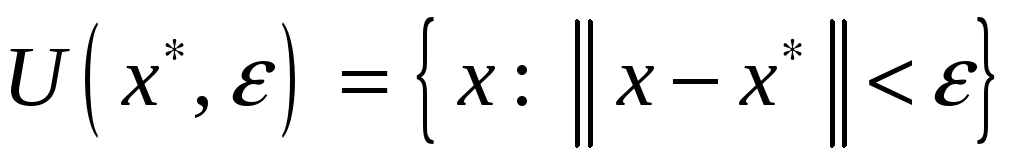.) Предположим

противное, то есть, что существует точка

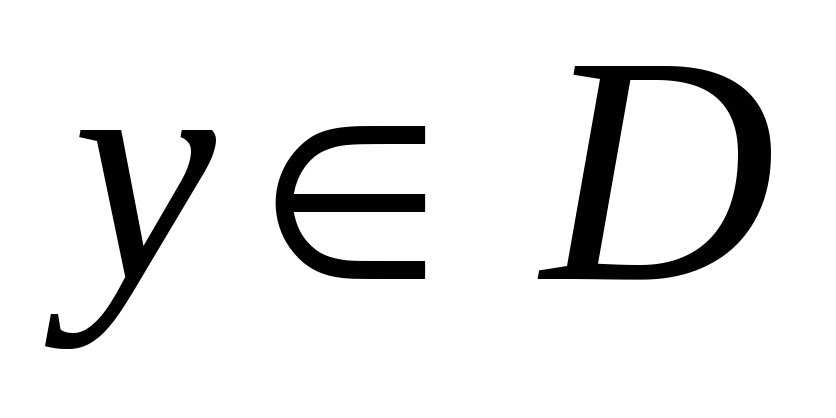
такая, что

. (2)

В силу выпуклости множества имеем

. Следовательно,

для достаточно

малых значений . Из неравенств (1), (2) и в силу выпуклости функции на множестве для таких имеем

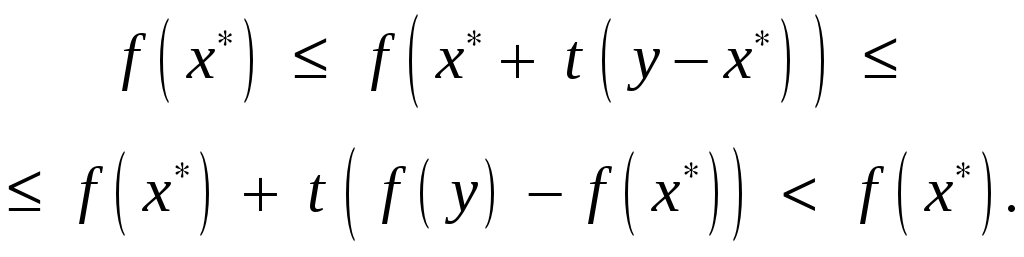
Полученное противоречие доказывает теорему.

Следующие две теоремы устанавливают свойства множества точек условного минимума.

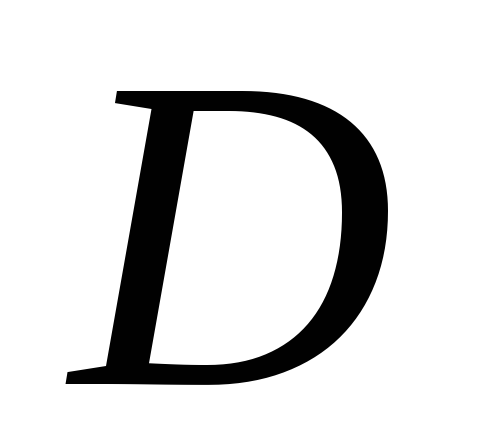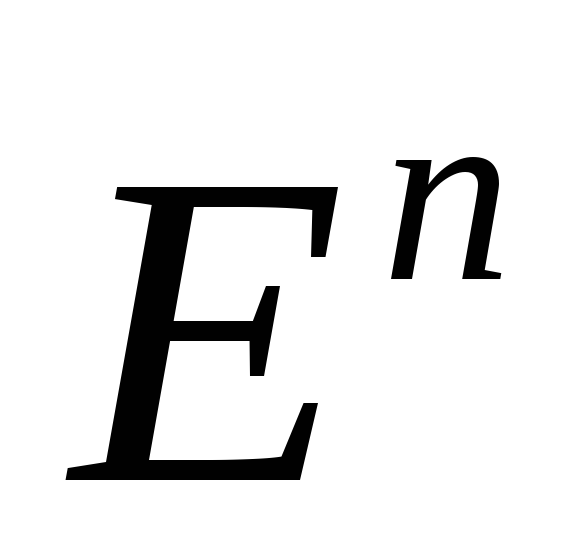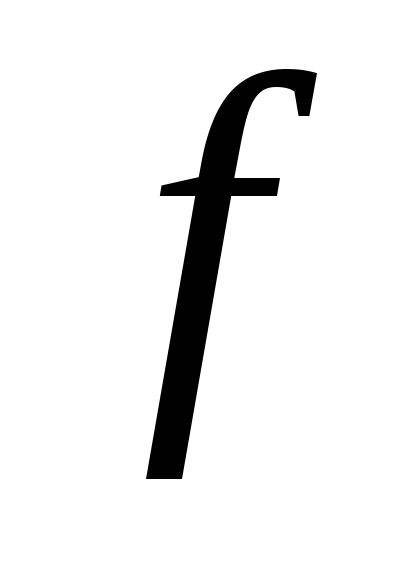Теорема 2. Пусть – выпуклое множество из , функция – выпукла н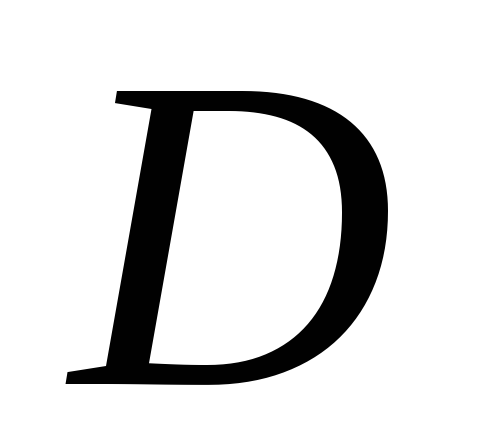а . Тогда 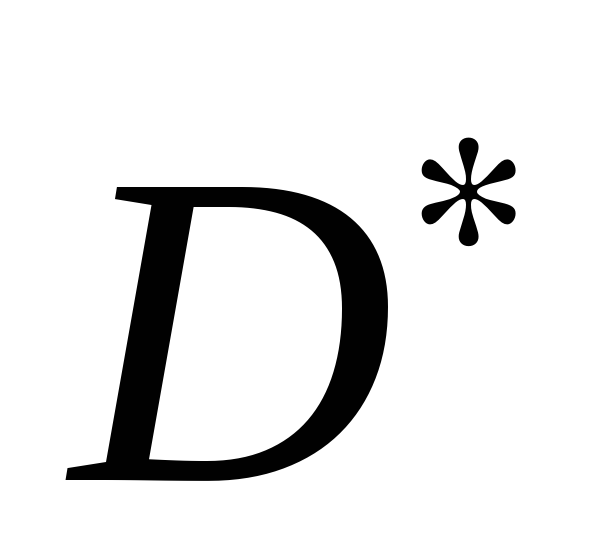– выпуклое множество.

Доказательство. Очевидно, что

.

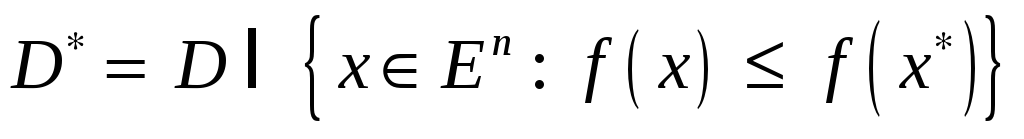Поэтому выпуклость множества 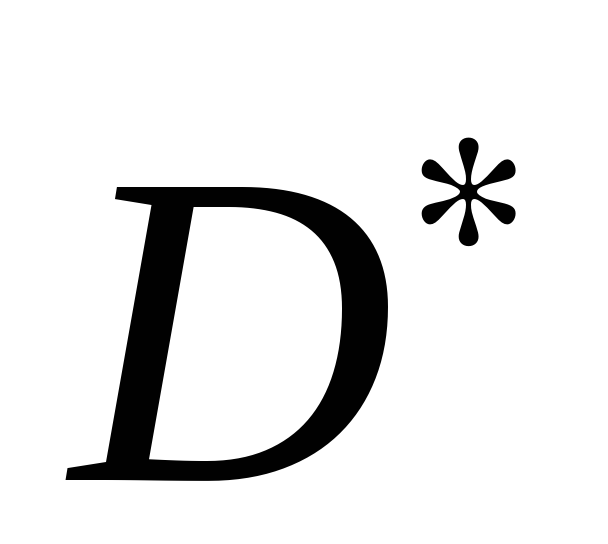следует из теорем 3.6 и 1.1.

Теорема 3. Пусть – выпуклое множество

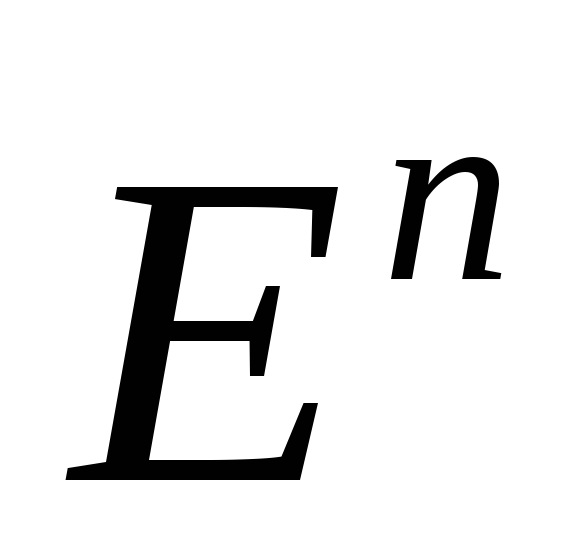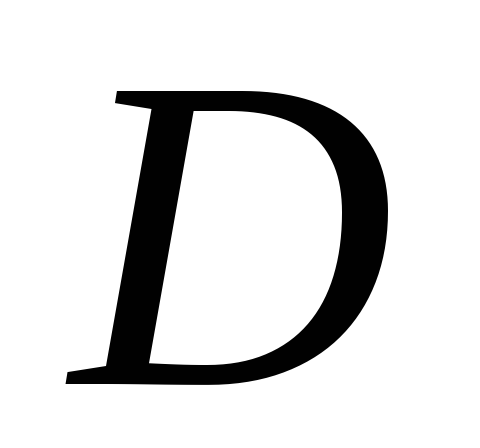из , функция – строго выпукла на . Тогда

множество 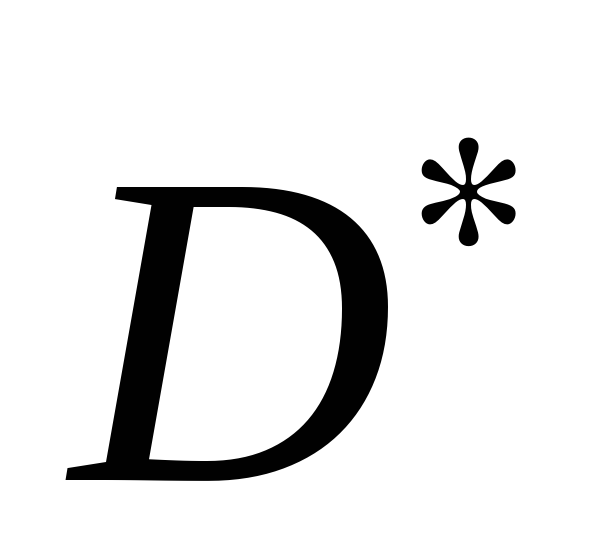содержит не более одной точки.

Доказательство. Пусть . Докажем, что оно состоит только из одной точки. Пусть это не так, то есть существуют два различных вектора . Тогда в силу выпуклости множества (см. предыдущую теорему) при любом , и в силу строгой выпуклости функции имеем

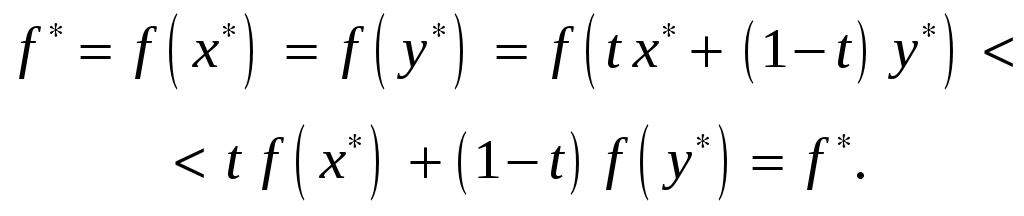
Полученное противоречие доказывает теорему.

Оставшаяся часть параграфа посвящена необходимым и достаточным условиям экстремума.

Теорема 4. (Критерий условного экстремума в терминах конусов условно релаксационных направлений) Пусть – выпуклое множество из , функция выпукла на . Тогда для того, чтобы точка была минимумом функции 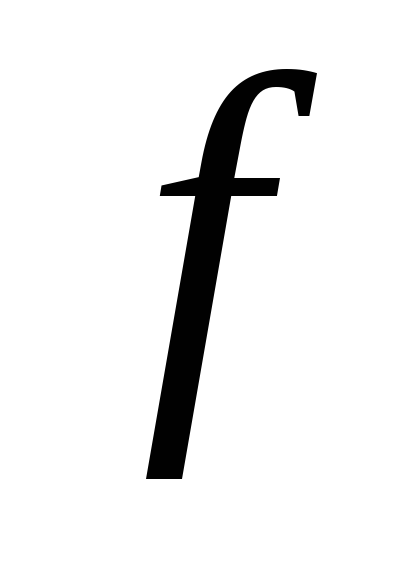на множестве 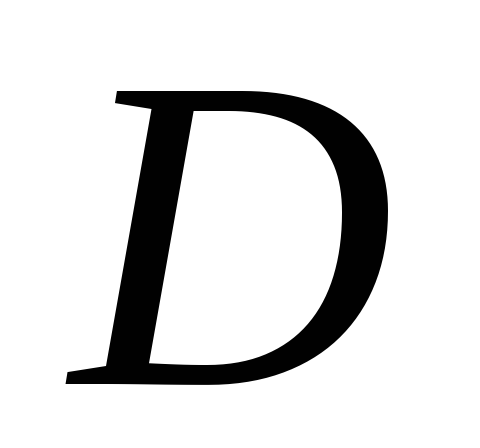, необходимо и достаточно, чтобы .

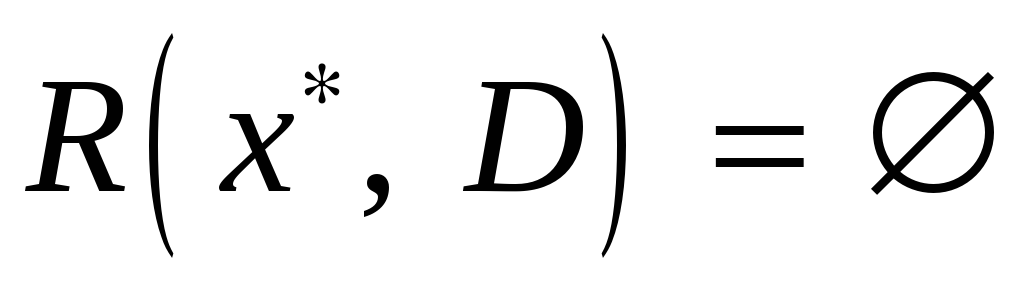Доказательство. Необходимость. Пусть –минимум функции на . Убедимся, что конус

. Предположим противное, то есть

существует вектор . Поскольку по определению , найдется число такое, что при всех имеем и . Таким образом, получено противоречие с тем, что – условный минимум.

Достаточность. Пусть . Докажем, что . Предположим противное. Пусть существует точка такая, что

. (3).

Обозначим . Согласно теореме 5.4 имеем . Учитывая неравенство (3) и выпуклость функции , получаем неравенства справедливые при всех . Значит, . Таким образом, . Полученное противоречие доказывает теорему.

Следствие. Пусть функция выпукла на . Тогда для того, чтобы точка была безусловным минимумом функции , необходимо и

достаточно, чтобы .

Справедливость этого утверждения следует

из того, что здесь и (см. параграф 5).

Теорема 5. (Критерий условного экстрему-

ма первого порядка) Пусть – выпуклое множество, дифференцируемая функция выпукла на . Тогда для того, чтобы точка была минимумом функции на множестве ,

необходимо и достаточно, чтобы выполнялось условие

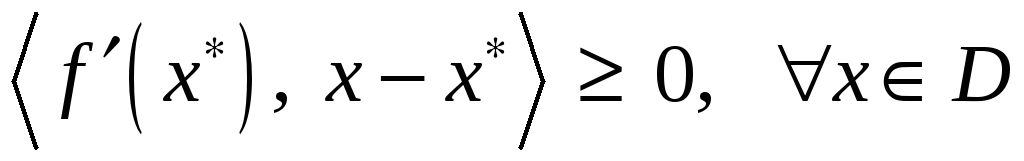. (4)

Справедливость этого утверждения следует из теорем 4, 5.2 и 5.4.

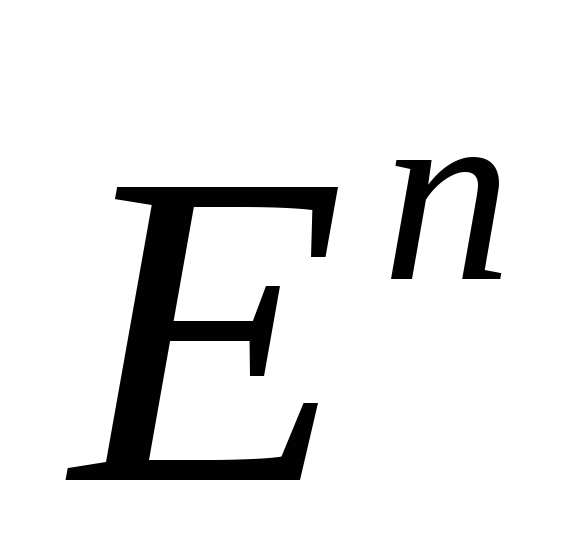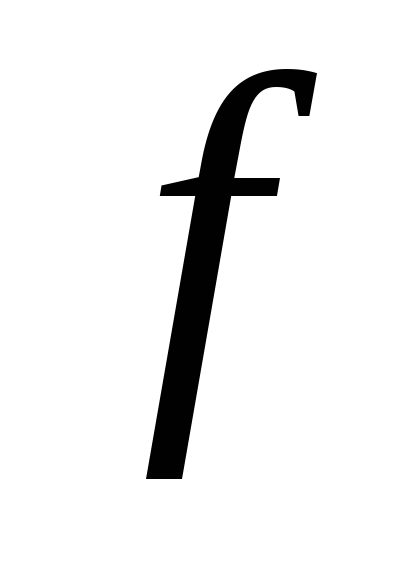Следствие. Пусть – выпуклая и дифференцируемая на функция. Тогда для того, чтобы точка была безусловным минимумом функции , необходимо и достаточно, чтобы .

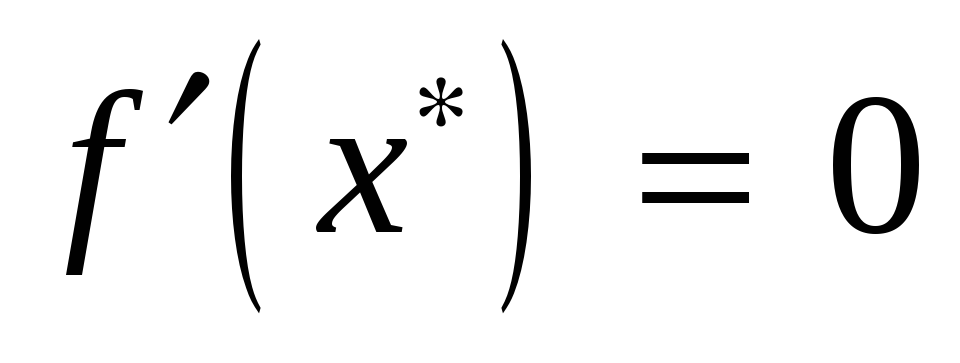Справедливость этого утверждения очевидным образом следует из (4) при .

38