
REVIZED / 5_Конусы_РВН
.docМетоды оптимизации: Часть I
5. Конусы релаксационных и возможных направлений
Определение
1. Пусть
функция
![]() определена на
определена на
![]() .
Вектор
.
Вектор
![]() называется релаксационным
направлением
(направлением
убывания)
функции
называется релаксационным
направлением
(направлением
убывания)
функции
![]() в точке
в точке
![]() ,
если существует число
,
если существует число
![]() такое, что для любого
такое, что для любого
![]() выполняется неравенство
выполняется неравенство
![]() .
.
Обозначим множество
релаксационных направлений функции
![]() в точке
в точке
![]() через
через
![]() .
.
Теорема 1.
Пусть функция
![]() выпукла на
выпукла на
![]() .
Тогда для любого
.
Тогда для любого
![]() множество
множество
![]() – выпуклый конус.
– выпуклый конус.
Доказательство.
Пусть
вектор
![]() ,
чи-сло
,
чи-сло
![]() .
Тогда согласно
определению 1 имеем
.
Тогда согласно
определению 1 имеем
![]() для любого
для любого
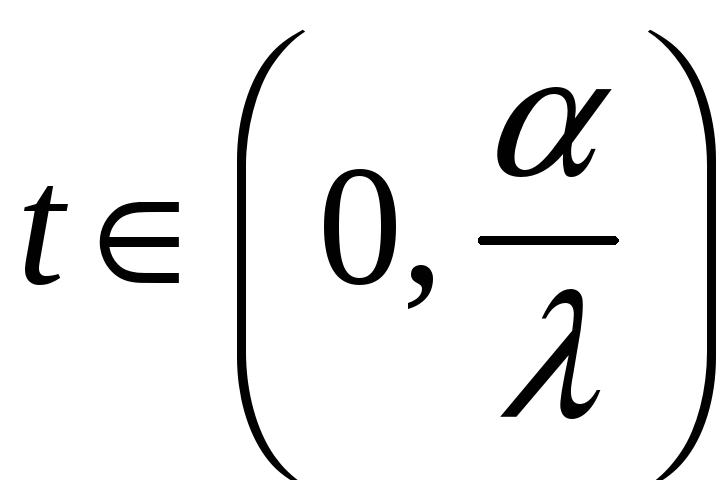 ,
то есть
вектор
,
то есть
вектор
![]() .
.
Проверим
теперь выполнение второго требования
определения выпуклого конуса. Пусть
векторы
![]() .
Согласно определению
1 найдутся
.
Согласно определению
1 найдутся
![]() такие, что
такие, что
![]() при всех
при всех
![]() и
и
![]() при всех
при всех
![]() .
Таким образом, оба
неравенства справедливы при всех
.
Таким образом, оба
неравенства справедливы при всех
![]() ,
где
,
где
![]() .
В силу выпуклости
функции
.
В силу выпуклости
функции
![]() имеем
имеем
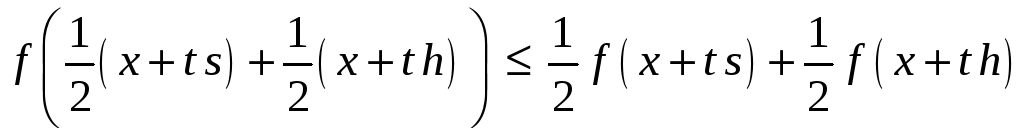 .
.
Следовательно,
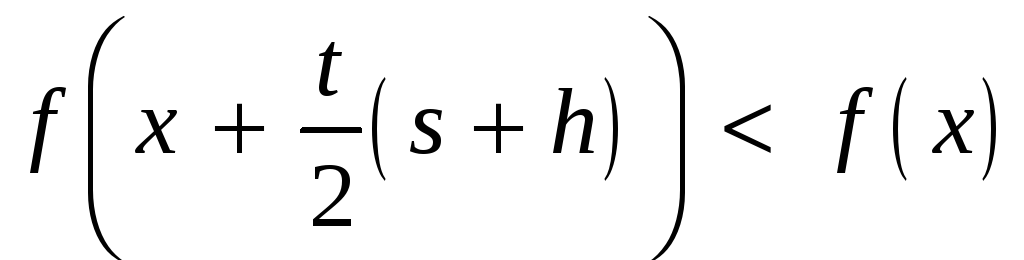 ,
то есть
,
то есть
![]() при всех
при всех
![]() ,
где
,
где
![]() .
Итак,
.
Итак,
![]() .
Что и требовалось.
.
Что и требовалось.
Релаксационные
направления часто используются как
при исследовании задач на минимум,
так и в различных методах решения
оптимиза-ционных задач. В случае,
когда решается задача максимизации,
используются направления
возрастания функции
в точке, удовлетворяющие неравенству
![]() при
при
![]() .
.
Определение 1 не всегда позволяет непосредственно отыскивать релаксационные направления функции или устанавливать их отсутствие. Для выпуклых дифференцируемых функций в этом может помочь следующая теорема.
Теорема 2.
Пусть
![]() – выпуклая дифференцируемая в точке
– выпуклая дифференцируемая в точке
![]() функция. Тогда
функция. Тогда
![]() .
(1)
.
(1)
Доказательство.
Докажем сначала
включение
![]() во множество
во множество
![]() .
Пусть
.
Пусть
![]() .
Тогда существует
.
Тогда существует
![]() такое, что
такое, что
![]() ,
,
![]() .
Из теоремы 4.1 получаем
.
Из теоремы 4.1 получаем
![]() .
Из этих двух неравенств и следует
.
Из этих двух неравенств и следует
![]() .
Что и требовалось.
.
Что и требовалось.
Докажем обратное включение.
Пусть имеет место неравенство
![]() .
Так как по условию функция
.
Так как по условию функция
![]() дифференцируема в точке
дифференцируема в точке
![]() ,
имеем
,
имеем
![]() ,
где
,
где
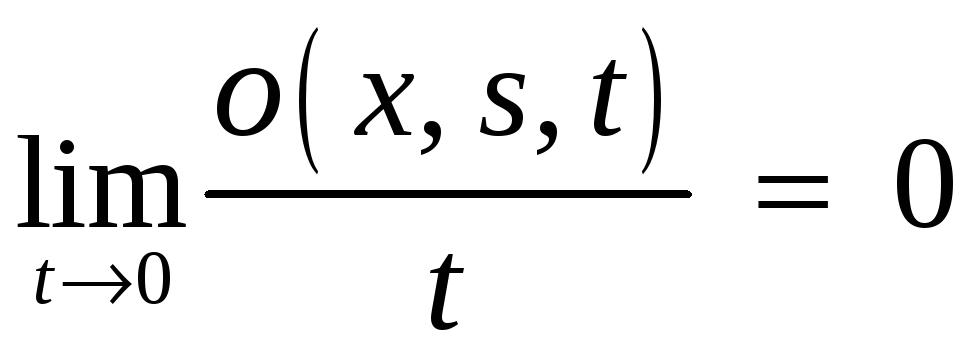 .
Поэтому для достаточно ма-лых
.
Поэтому для достаточно ма-лых
![]() знак приращения функции
знак приращения функции
![]() совпадает со знаком произведения
совпадает со знаком произведения
![]() .
Тогда существует
.
Тогда существует
![]() такое, что
такое, что
![]() ,
,
![]() ,
то есть
,
то есть
![]() .
Что и требовалось.
.
Что и требовалось.
Заметим, что при доказательстве второго включения выпуклость функции не использовалась.
Заметим также, что в условиях теоремы 2
при
![]() конус
конус
![]() является открытым полупространством.
является открытым полупространством.
Наконец,
легко увидеть, что если функция
![]() вогнута и дифференцируема
в точке
вогнута и дифференцируема
в точке
![]() ,
то вектор
,
то вектор
![]() является направлением возрастания
функции
является направлением возрастания
функции
![]() в точке
в точке
![]() тогда и только тогда, когда выполняется
неравенство
тогда и только тогда, когда выполняется
неравенство
![]() .
.
В случае, когда функция
![]() линейна (
линейна (![]() ),
а значит, выпукла и вогнута одновременно,
неравенство
),
а значит, выпукла и вогнута одновременно,
неравенство
![]() задает конус направлений убывания, а
задает конус направлений убывания, а
![]() – конус направлений возрастания в
любой точке
– конус направлений возрастания в
любой точке
![]() .
.
Определение 2.
Пусть
![]() – множество из
– множество из
![]() ,
точка
,
точка
![]() .
Вектор
.
Вектор
![]() называется возможным
направлением в
точке
называется возможным
направлением в
точке
![]() для множества
для множества
![]() ,
если существует число
,
если существует число
![]() такое, что
такое, что
![]() для любого
для любого
![]() .
.
Обозначим множество возможных
направлений в точке
![]() для множества
для множества
![]() через
через
![]() .
.
Теорема 3.
Пусть
![]() – выпуклое множество,
– выпуклое множество,
![]() .
Тогда
.
Тогда
![]() – выпуклый конус.
– выпуклый конус.
Доказательство.
Пусть
вектор
![]() ,
число
,
число
![]() .
Тогда согласно
определению 1 имеем
.
Тогда согласно
определению 1 имеем
![]() для любого
для любого
![]() ,
то есть
вектор
,
то есть
вектор
![]() .
.
Проверим
теперь выполнение второго требования
определения выпуклого конуса. Пусть
векторы
![]() .
Согласно определению
2 найдутся
.
Согласно определению
2 найдутся
![]() такие, что
такие, что
![]() при всех
при всех
![]() и
и
![]() при всех
при всех
![]() .
Таким образом, эти
включения справедливы при всех
.
Таким образом, эти
включения справедливы при всех
![]() ,
где
,
где
![]() .
В силу выпуклости
множества
.
В силу выпуклости
множества
![]() имеем
имеем
![]() ,
то есть
,
то есть
![]() при всех
при всех
![]() ,
где
,
где
![]() .
Таким образом,
.
Таким образом,
![]() .
Что и требовалось.
.
Что и требовалось.
Заметим,
что если
![]() ,
то
,
то
![]() .
.
Теорема 4.
Если
![]() – выпуклое множество,
точки
– выпуклое множество,
точки
![]() ,
то
вектор
,
то
вектор
![]() .
.
Справедливость этого утверждения непосредственно следует из определений выпуклого множества и возможного направления.
При исследовании задач на условный экстремум нам понадобятся так называемые условно релаксационные направления.
Определение 3.
Пусть функция
![]() определена на множестве
определена на множестве
![]() ,
точка
,
точка
![]() .
Вектор
.
Вектор
![]() называется условно
релаксационным направлением
функции
называется условно
релаксационным направлением
функции
![]() в точке
в точке
![]() относительно множества
относительно множества
![]() ,
если в этой точке направление
,
если в этой точке направление
![]()
является
возможным для
![]() и релаксационным для функции
и релаксационным для функции
![]() .
.
Обозначим множество условно
релаксационных направлений функции
![]() в точке
в точке
![]() через
через
![]() .
Итак,
.
Итак,
![]() ,
а значит, в условиях теорем 1 и 3
множество
,
а значит, в условиях теорем 1 и 3
множество
![]() является выпуклым конусом.
является выпуклым конусом.
6. экстремальные свойства выпуклых функций
Данный параграф посвящен изучению экстремумов выпуклых функций на выпуклых множествах. Из теорем, с которыми мы здесь познакомимся, следует, что этот класс задач на экстремум удобен для исследования и решения.
Теорема
1.
Пусть
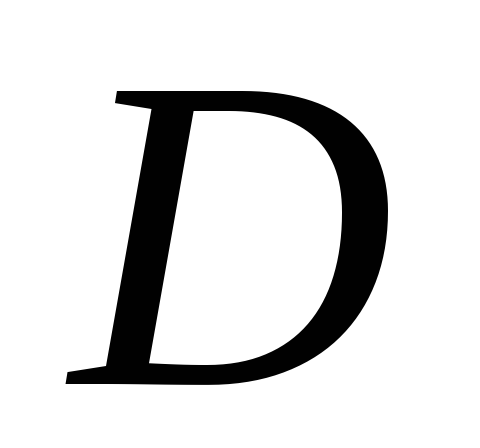 – выпуклое множество из
– выпуклое множество из
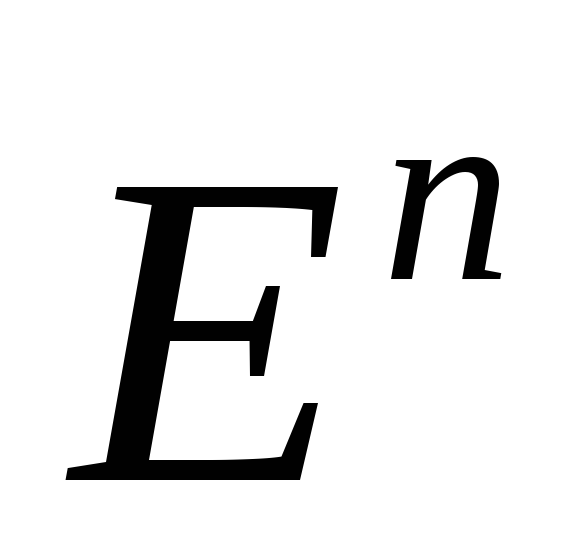 ,
функция
,
функция
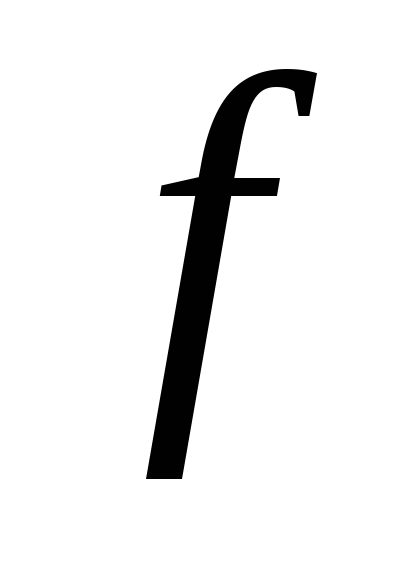 – выпукла на
– выпукла на
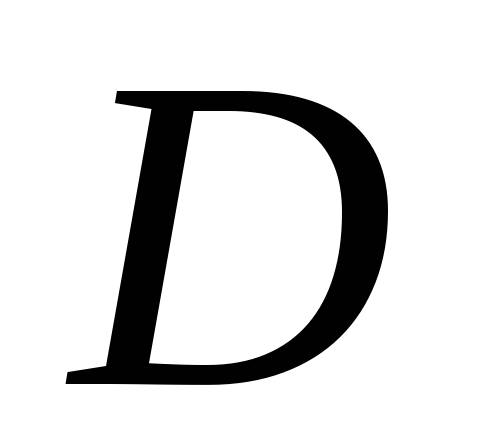 .
Тогда всякий локальный условный
минимум функции
.
Тогда всякий локальный условный
минимум функции
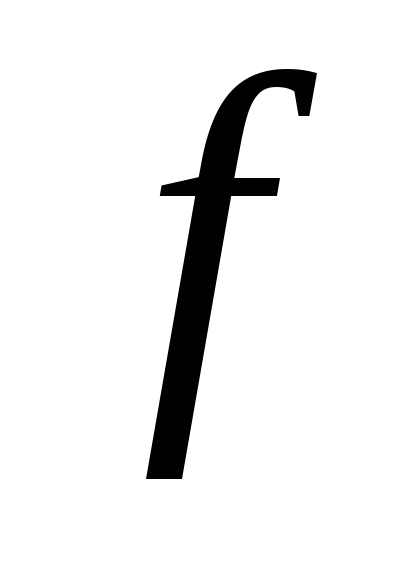 на
множестве
на
множестве
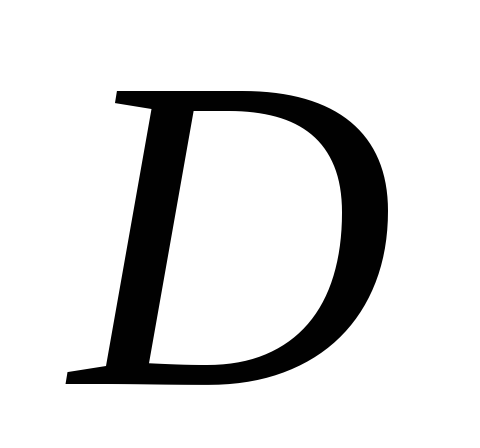 является
и глобальным.
является
и глобальным.
Доказательство.
Пусть
 –
точка локального минимума функции
–
точка локального минимума функции
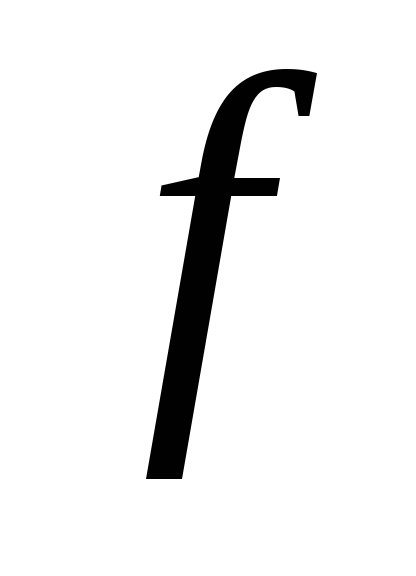 на множестве
на множестве
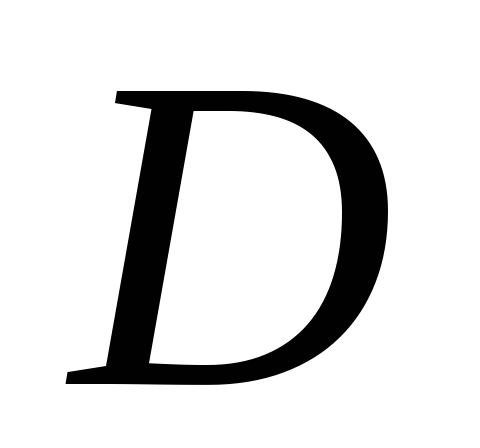 .
Тогда существует такое число
.
Тогда существует такое число
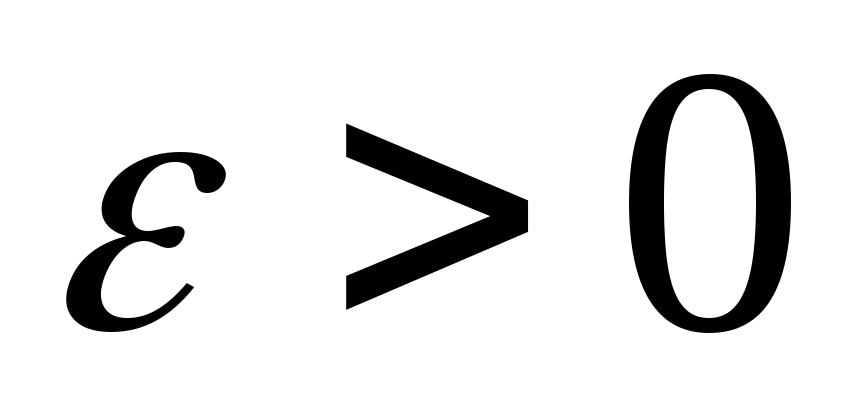 ,
что для всех
,
что для всех
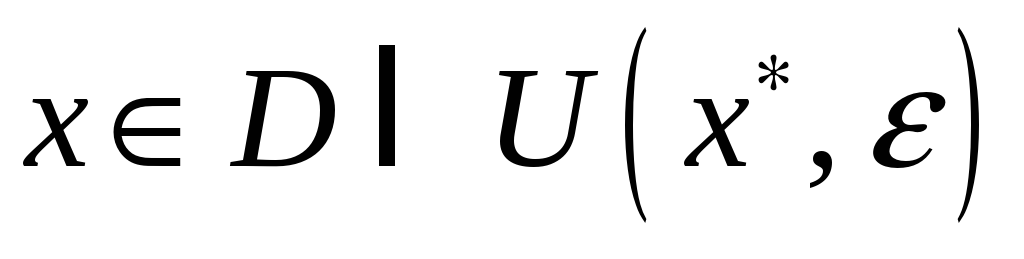 выполняется
неравенство
выполняется
неравенство
![]() .
(1)
.
(1)
(Здесь
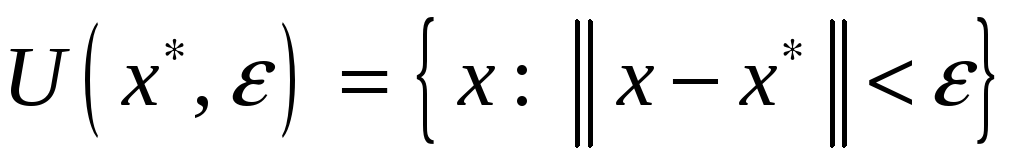 .)
Предположим
.)
Предположим
противное,
то есть, что существует точка
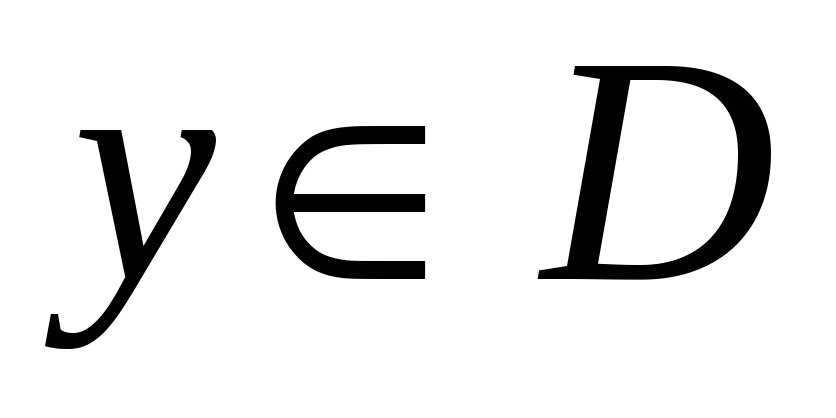
такая, что
![]() .
(2)
.
(2)
В силу выпуклости множества
![]() имеем
имеем
![]() .
Следовательно,
.
Следовательно,
![]() для достаточно
для достаточно
малых
значений
![]() .
Из неравенств (1), (2) и в силу выпуклости
функции
.
Из неравенств (1), (2) и в силу выпуклости
функции
![]() на множестве
на множестве
![]() для таких
для таких
![]() имеем
имеем
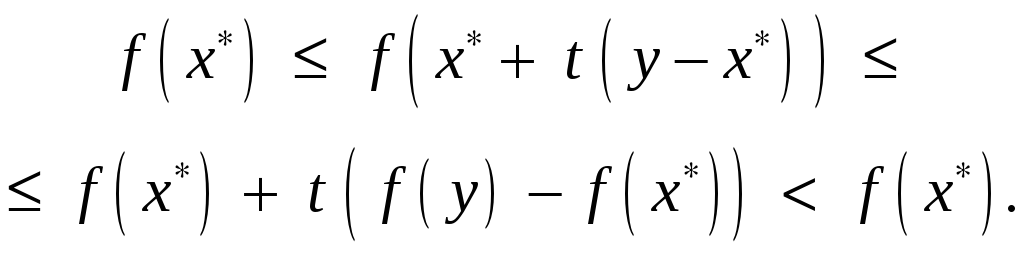
Полученное противоречие доказывает теорему.
Следующие
две теоремы устанавливают свойства
множества
![]() точек условного минимума.
точек условного минимума.
Теорема
2.
Пусть
 – выпуклое множество из
– выпуклое множество из
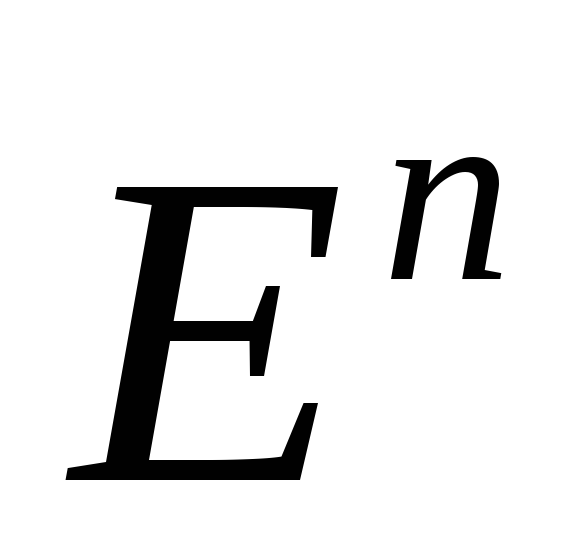 ,
функция
,
функция
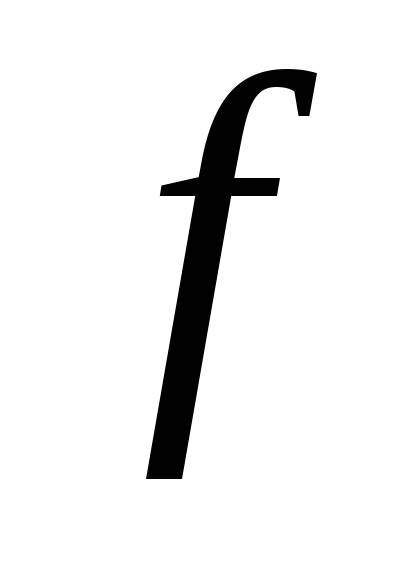 – выпукла на
– выпукла на
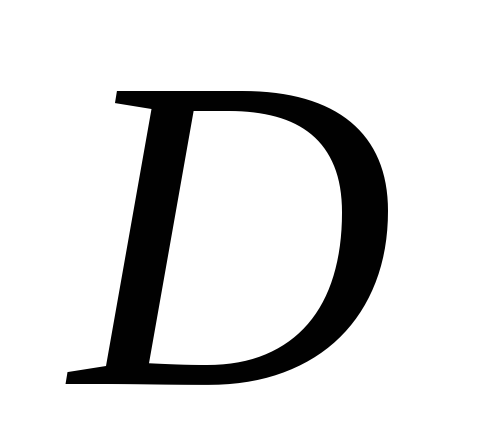 .
Тогда
.
Тогда
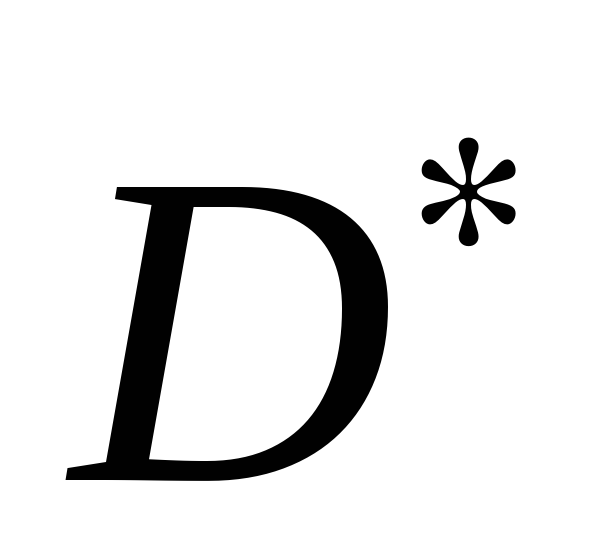 – выпуклое множество.
– выпуклое множество.
Доказательство. Очевидно, что
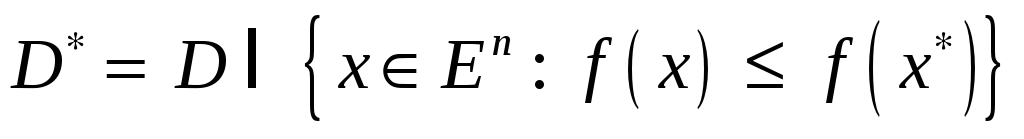 .
.
Поэтому
выпуклость множества
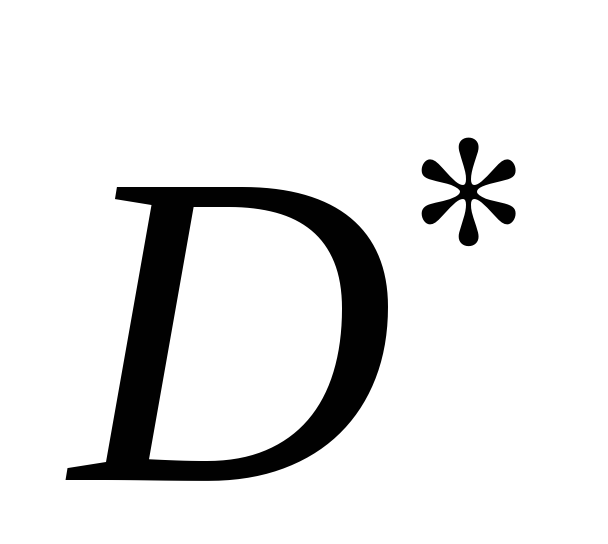 следует из теорем 3.6 и 1.1.
следует из теорем 3.6 и 1.1.
Теорема 3.
Пусть
![]() – выпуклое множество
– выпуклое множество
