
3_Выпуклые функции_сент_9_2008
.rtf
Выпуклые функции
Определение
1.
Функция
 ,
определенная на
,
определенная на
 ,
называется выпуклой,
если для любых
,
называется выпуклой,
если для любых
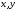 и любого
и любого
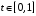 выполняется неравенство
выполняется неравенство
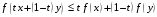 .
(1)
.
(1)
Если
при
 и
и
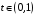 неравенство (1)
выполняется как строгое, то функция
неравенство (1)
выполняется как строгое, то функция
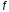 называется строго
выпуклой.
называется строго
выпуклой.
Определение
2.
Функция
 ,
определенная на
,
определенная на
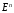 ,
называется вогнутой
(строго
вогнутой),
если функция (
,
называется вогнутой
(строго
вогнутой),
если функция (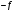 )
является выпуклой (строго выпуклой).
)
является выпуклой (строго выпуклой).
Очевидно, что любая строго выпуклая (строго вогнутая) функция является выпуклой (вогнутой) функцией, но не наоборот.
Приведем некоторые операции допустимые в классе выпуклых функций.
Теорема
1.
Пусть все функции
 ,
,
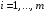 ,
,
выпуклы
на
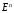 ,
числа
,
числа
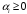 .
Тогда функция
.
Тогда функция
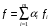 также выпукла.
также выпукла.
Доказательство.
Пусть заданы векторы
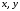 и число
и число
 .
Так как функции
.
Так как функции
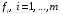 ,
выпуклы, то для всех
,
выпуклы, то для всех
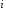 выполняются неравенства
выполняются неравенства
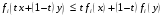 .
Умножая эти неравенства на неотрицательные
величины
.
Умножая эти неравенства на неотрицательные
величины
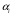 и суммируя их по
и суммируя их по
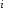 ,
получим неравенство
,
получим неравенство
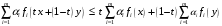 .
.
Следовательно,
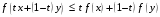 .
Что и требовалось.
.
Что и требовалось.
Теорема
2.
Пусть на
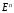 определены функции
определены функции
 ,
,
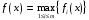 .
Если все
.
Если все
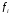 – выпуклые, то функция
– выпуклые, то функция
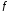 также выпуклая.
также выпуклая.
Доказательство.
Пусть заданы векторы
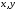 и число
и число
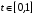 .
Так как функции
.
Так как функции
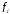 выпуклы, то для всех
выпуклы, то для всех
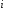 выполняются неравенства
выполняются неравенства
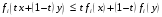 .
Следовательно,
.
Следовательно,
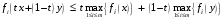
для
всех
 .
Из полученных неравенств имеем
.
Из полученных неравенств имеем
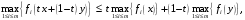
то
есть
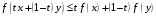 .
Что и требовалось.
.
Что и требовалось.
Приведем теоремы о суперпозициях выпуклых функций.
Теорема
3.
Пусть функция
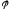 определена на отрезке
определена на отрезке
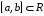 и является на нем выпуклой и
неубывающей; функция
и является на нем выпуклой и
неубывающей; функция
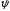 выпукла на выпуклом множестве
выпукла на выпуклом множестве
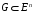 ,
,
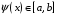 ,
,
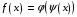 для всех
для всех
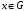 .
Тогда функция
.
Тогда функция
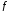 выпукла на
выпукла на
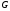 .
.
Доказательство.
Пусть
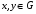 ,
,
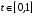 .
Тогда
.
Тогда
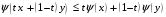 в силу выпуклости функции
в силу выпуклости функции
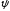 на
на
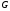 .
Очевидно, что
.
Очевидно, что
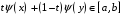 .
Поэтому, а также в силу монотонности
и выпуклости
.
Поэтому, а также в силу монотонности
и выпуклости
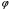 на
на
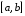 ,
имеем
,
имеем

Следовательно,
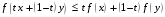 .
Что и требовалось.
.
Что и требовалось.
Теорема
4.
Пусть
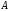 – матрица размерности
– матрица размерности
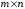 ,
,
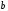 – вектор размерности
– вектор размерности
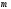 ,
,
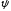 – функция, определенная и выпуклая
на многообразии
– функция, определенная и выпуклая
на многообразии
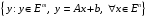 ,
,
 .
Тогда функция
.
Тогда функция
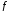 выпукла на
выпукла на
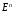 .
.
Доказательство.
Пусть заданы векторы
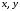 и число
и число
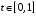 .
Тогда имеем
.
Тогда имеем
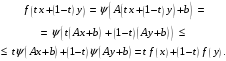
Что и требовалось.
Далее
покажем, что выпуклость функции многих
переменных можно установить, исследуя
на выпуклость ее сужения на всевозможные
прямые в
 .
Выпуклость функции одной переменной
установить зачастую значительно проще,
чем выпуклость функции многих
переменных.
.
Выпуклость функции одной переменной
установить зачастую значительно проще,
чем выпуклость функции многих
переменных.
Пусть
заданы функция
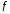 и
векторы
и
векторы
 .
Сужение
.
Сужение
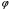 функции
функции
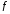 на
прямую
на
прямую
 определим
следующим образом:
определим
следующим образом:
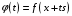 .
(2)
.
(2)
Теорема
5.
Функция
 является выпуклой тогда и только
тогда, когда выпуклой является и
функция
является выпуклой тогда и только
тогда, когда выпуклой является и
функция
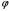 ,
определенная по формуле (2)
при
любых
,
определенная по формуле (2)
при
любых
 .
.
Доказательство.
Необходимость.
Пусть
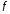 –
выпуклая функция,
–
выпуклая функция,
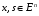 .
Покажем,
что функция
.
Покажем,
что функция
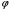 также
является выпуклой. Пусть
также
является выпуклой. Пусть
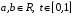 .
Тогда
.
Тогда
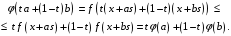
Достаточность.
Предположим, что для произвольных
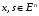 функция
функция
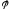 – выпуклая. Пусть
– выпуклая. Пусть
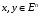 и
и
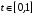 .
Тогда
.
Тогда
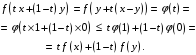
Что и требовалось.
Далее установим связь между выпуклыми множествами и выпуклыми функциями.
Пусть
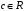 – некоторая константа. Множество
– некоторая константа. Множество
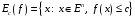 называется лебеговым
множеством функции
называется лебеговым
множеством функции
 .
.
Теорема
6.
Пусть функция
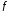 выпукла на
выпукла на
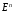 .
Тогда любое ее лебегово множество
выпукло.
.
Тогда любое ее лебегово множество
выпукло.
Доказательство.
Пусть
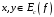 ,
,
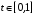 .
Тогда из
.
Тогда из
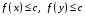 и в силу выпуклости
и в силу выпуклости
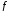
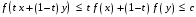 .
.
Таким
образом,
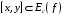 ,
что и означает выпуклость множества
,
что и означает выпуклость множества
 .
.
Эта теорема устанавливает одностороннюю связь между выпуклыми множествами и выпуклыми функциями. Утверждение, обратное теореме 6, не имеет места.
