
Учебник. Двигатели внутреннего сгорания теория, моделирование и расчёт процессов / DVS_teoriy_modelir_i_raschet_processov2
.pdf
dp |
+ |
|
k |
p = |
(k −1)qz |
|
dx |
; |
(12. 48) |
dν |
ν |
ν |
|
dν |
|||||
в котором k = Сp / Сv – отношение теплоёмкостей.
Нас интересует уравнение для определения давлений рабочего тела в период горения. То есть, необходимо знать уравнение, которое определяло бы давление как функцию времени. Такое уравнение можно получить на основа-
нии (12. 48).
Пусть t – текущее время, а α – соответствующий ему угол поворота коленчатого вала. Напомним, что между α и t существует связь: α = 6nt .
Для скорости изменения удельного объёма рабочего тела имеем ddtν = ddαν ω ,
где ω – угловая скорость.
Отсюда
dν = ddαν ω dt .
После соответствующей подстановки выражения для dv в уравнение (12. 48) и умножения обеих его частей на ωdv/dα получим уравнение, которое можно решить относительно скорости изменения давления в период горения. Получим
dp |
|
(k −1)qz |
|
dx |
|
k |
|
dν |
|
|
|
= |
|
− |
|
dt |
|
p , |
(12. 49) |
||||
dt |
ν |
|
dt |
|
ν |
|
|||||
|
|
|
|
|
|
|
|||||
где dx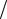 dt – скорость изменения доли сгоревшего топлива во времени. В соответствии с (7. 14)
dt – скорость изменения доли сгоревшего топлива во времени. В соответствии с (7. 14)
|
|
|
|
|
|
|
|
|
m |
|
tг |
m+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
+ |
|
t |
|
|
|
−6,908 |
|
|
|
|
|
dx |
|
6,908(m |
1) |
г |
|
|
|
|
|
|||||
= |
|
|
|
e |
tz |
, |
(12. 50) |
|||||||
dt |
t z |
|
|
|
|
|
|
|
|
|
||||
|
|
|
t z |
|
|
|
|
|
|
|||||
где tг – время, отсчитываемое от начала горения.
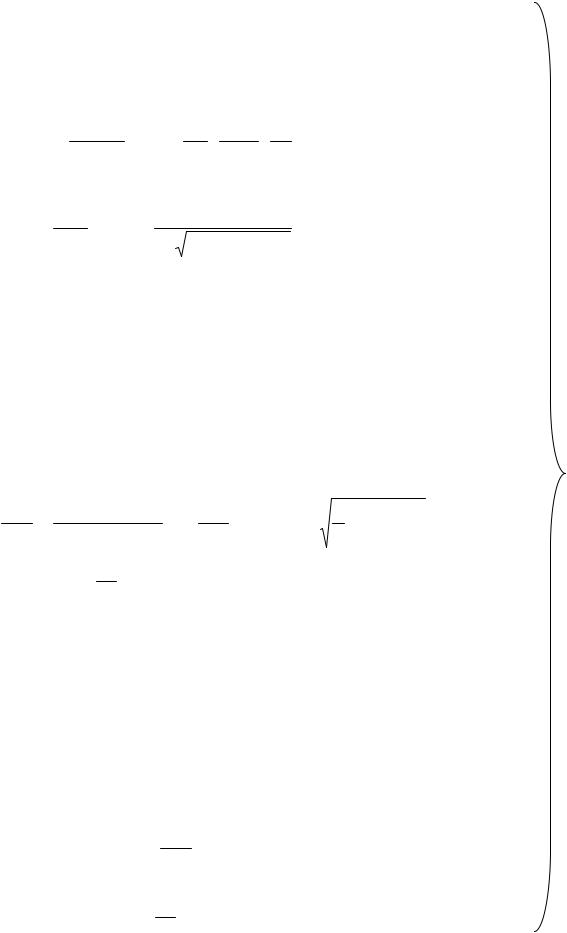
Выражение (12. 49) является, по существу, уравнением динамики сгорания, записанным в дифференциальной форме. Использование его позволяет комплексную взаимосвязь процессов, протекающих в двигателе с автоматическим регулированием ε, описать системой уравнений, которая обозначена как
(12. 55).
321
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
dν |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
dp |
|
|
|
(k − |
1)q |
z |
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n p dν |
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
p σ1 + |
|
− |
|
|
1 |
|
|
|
|
|
|
σ |
2 , |
(12. 51) |
||||||||||||||||||
dt |
|
|
|
|
|
v |
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
ν |
|
|
|
|
dt |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ν |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
νа |
dε |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
dν |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ν |
α σ(α) |
|
|
dε |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
= − |
|
|
ωε 2 |
|
|
|
ψ(α) + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
dt |
|
|
|
|
|
|
ε |
|
|
|
2ω |
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
ε |
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
λ sin 2α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
(12.52) |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
sinα + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωσ |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
1− λ |
2 |
|
sin |
2 |
α |
|
|
|
3 |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
dε |
= − |
|
|
|
|
|
|
|
Vh F |
|
|
|
|
|
|
|
|
|
|
dxп |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(12. 41) |
|||||||||||||||||||
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
Vh |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
ε0 −1 |
+ xпF |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
dx |
|
|
|
6,908(m +1) |
tг |
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
tг |
m+1 |
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
exp |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
(12.50) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
dt |
|
|
|
|
|
|
|
|
tz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− 6,908 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tz |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(12. 55) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dpв |
= β(V |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dxп |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
( pв − p0 ) − |
|||||||||||||||||||||||
dt |
|
|
|
− x |
п |
F |
) |
Fп |
|
|
|
dt |
|
|
|
− µ |
fкл.щ γ |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
п |
|
|
|
|
|
|
|
|
п |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(12.31) |
||||||
|
|
|
|
− fкл.с |
dt |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
du |
= − |
|
|
1 |
[P |
jоб |
|
+ pF + σR |
тр.н |
− |
R |
тр.вн |
|
+ σR |
− |
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
dt |
|
|
|
|
|
|
mоб |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
− pвFп + pмFк.п − p0Fк + Pjм.в], |
|
|
|
|
|
|
|
(12.53) |
|||||||||||||||||||||||||||||||||||||||||||||||
duкл |
|
|
= − |
|
1 |
[ Pо.пр + Pjкл + yC′ − pв fкл − |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
dt |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
m кл |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
− 0,45( pв − pо) fкл.доп ], |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(12.54) |
||||||||||||||||||||||||||||||||||
dxdtп = u ,
dydt = uкл
322
В системе (12. 55) σ, σ1, σ2 и σ3 – ступенчатые функции. Они введены для сокращения записи и обеспечения компактности математической модели. Так что в том виде, в котором записана система дифференциальных уравнений, она пригодна для расчёта параметров процессов в течение всего периода работы клапана (вне зависимости от того, начался, идёт или закончился процесс горения).
σ1 |
= 0 |
|
σ2 |
, если игла клапана отрывается от седла приα ≤αy . |
|
=1 |
|
|
Наоборот, |
|
|
σ1 |
=1 |
, если игла отрывается от седла при α ≥αy , то есть, в про- |
σ2 |
|
|
= 0 |
|
|
цессе сгорания.
σ= −1 при 00 ≤ α ≤1800 ;
σ3 =1
σ =1 |
при −1800 ≤ α ≤ 00 . |
|
|
σ3 = −1 |
|
Первый член в правой части уравнения (12. 51) представляет собой уравнение динамики сгорания, а вторым отображается динамика изменения давления в случае политропического сжатия рабочего тела.
Уравнения (12. 53) и (12. 54) являются уравнениями динамического равновесия оболочки поршня и клапана соответственно, которые в данном случае
переписаны относительно du/dt и duкл/dt.
Таким образом, совокупность процессов, протекающих в двигателе с автоматическим регулированием ε, описывается системой неоднородных дифференциальных уравнений первого порядка. Система существенно нелинейна: она содержит нелинейности типа «корень квадратный», ступенчатые функции и другие функциональные нелинейности. Все они объясняются физической сущностью процессов. Например, перемещение иглы клапана ограничено: 0 ≤ у ≤ умакс. Вообще говоря, ограниченно и перемещение оболочки поршня: оно определяется пределами регулирования степени сжатия (εмин ≤ ε ≤ εмакс). И с этим необходимо считаться в случаях, когда рассматривается режим сброса или набора нагрузки.
В связи с существенными нелинейностями рассматриваемая система в конечном виде проинтегрирована быть не может. Во всяком случае, интегрирование её в том виде, в котором она записана, представляет значительные трудности. Поэтому для её решения используются численные методы.
323

Рассмотрим случай работы, когда условие (12. 45) не выполняется для –1800 ≤ α ≤ αу. Тогда, начиная с α = αу интегрируется система
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dν |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dp |
|
|
(k |
−1)qz |
|
|
|
dx |
|
|
|
k dt |
|
|
|
|
|
|
|
|
|
|
||||||||
= |
|
|
|
− |
|
, |
|
|
|
|
|
|
|
|
|
|||||||||||||||
dt |
|
|
ν |
|
|
|
dt |
|
ν |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ν |
|
|
|
(ε |
− |
1) |
|
|
|
|
|
|
|
|
λ |
|
|
|
|
α |
|
|
|
||||||
d |
|
= |
α |
2ε |
|
|
|
|
|
sin |
α + |
|
|
sin 2 |
2 |
|
ωσ3 , . |
(12. 56) |
||||||||||||
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 − λ |
2 |
sin |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
tг |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
+ |
|
|
t |
|
|
|
|
−6,908 |
|
|
|
|
|
|
|
|
|
|||||
dx |
|
6,908(m |
1) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
= |
|
|
|
|
|
г |
|
e |
|
tz |
|
|
|
|
|
|||||||||||||||
dt |
|
|
|
t z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
t z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Она также решается численным методом. При решении её за начальные условия принимаются значения параметров в точке y индикаторной диаграммы,
то есть, р0 = ру; v0 = vy; х0 = 0; tг = 0.
Решение (12. 56) ведётся до выполнения условия (12. 45), после чего правомерной становится система (12. 55). Начальными условиями для неё являются численные значения p, v и х, определенные по (12. 56); за рво принимается его величина, определённая по условию равновесия оболочки в момент, соответствующий выполнению (12. 45). Начальное значение ε принимается равным ε0, а u0, xп0, uкл0 и у0 принимаются равными нулю.
Текущие значения отношения теплоёмкостей k определяются по уравнениям, приведенным в разделе 7.
С момента закрытия сливного клапана, что определяется неравенством
pв fкл − Pjкл + 0,45( pв − p0 ) fкл.доп ≤ Pо.пр |
(12. 57) |
степень сжатия не меняется, ибо с этого момента u = 0, uкл = 0 и dε/dt = 0. Оболочка не перемещается. Соответствующие величины параметров при выполнении (12. 57) принимаются за начальные. А характер протекания p,ν и x , устанавливается по (12. 56), которая становится правомерной до α = αz .
С точки z начинается процесс «чистого» расширения. При «чистом» расширении характер протекания параметров определяется системой уравнений
dp = − n2 p dν , |
|
|
|
|
|
|
|
|
|
||||
dt |
|
ν |
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
(12. 58) |
||||
dν |
|
ν |
α |
(ε −1) |
|
|
λ sin 2α |
|
|
|
|||
= − |
|
|
ω |
|
|
||||||||
|
|
|
sinα + |
|
|
2 |
2 |
|
|
|
|||
dt |
|
|
|
2ε |
|
2 |
1 − λ |
|
|
|
|
||
|
|
|
|
sin |
|
α |
|
|
|
||||
где αz ≤α ≤1800 .
324
При решении (12. 58) за начальные значения параметров принимаются их величины в точке z индикаторной диаграммы.
Так рассчитывается рабочий цикл дизеля с автоматическим регулированием степени сжатия.
Изложенное позволяет заключить, что динамическая модель рабочего цикла дизеля с ПАРСС представлена системой обыкновенных дифференциальных уравнений первого порядка, полученных на основании положений теории двигателей, термодинамики, гидродинамики и механики. Ею описываются динамика движения оболочки поршня в период насосных ходов, в тактах сжатия и расширения. Она включает уравнения динамического равновесия оболочки и иглы сливного клапана; уравнения динамики сгорания и неразрывности жидкости; уравнения для степени сжатия и удельного объёма рабочего тела.
При расчёте рабочего цикла описанным способом граничными условиями являются конструктивные параметра поршня. В частности, эти условия за-
ключаются в следующем: 0 ≤ у ≤ умакс, а εмин ≤ ε ≤ εмакс. Ограничения умакс, εмин и εмакс задаются в исходных данных.
К исходным данным относятся следующие:
1. Частота вращения коленчатого вала, об/мин . . . . . . . . . . . . . . . . . . . . . . . . . n
2. Радиус кривошипа . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . r
3. Отношение радиуса кривошипа к длине шатуна. . . . . . . . . . . . . . . . . . . . . . . λ 4. Масса оболочки. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . mоб
5. Масса масла в верхней полости поршня (начальное значение) . . . . . . . . . mм.в 6. Масса масла в нижней полости поршня (начальное значение) . . . . . . . . . mм.в 7. Масса деталей, совершающих возвратно-поступательное движение (включа-
ется и масса шатуна) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . mп 8. Давление остаточных газов . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . pr
9. Давление наддува . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . рк 10. Диаметр цилиндра . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . D
11. Коэффициент трения поршневых колец о стенки цилиндра . . . . . . . . . . . . k0
12. Число поршневых колец. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . i 13. Высота поршневого кольца. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . h
14. Давление поршневого кольца на стенку, создаваемое силами упругости . рр 15. Коэффициент трения оболочки о стержень поршня . . . . . . . . . . . . . . . . . . к1
16. Коэффициент трения оболочки о стенку цилиндра . . . . . . . . . . . . . . . . . . . к2
17. Давление в главной масляной магистрали двигателя . . . . . . . . . . . . . . . . . . рм 18. Диаметр рабочей поверхности верхней гидравлической полости . . . . . . . D1
19. Диаметр нижней гидравлической полости поршня (меньший из двух – см.
рис. 12. 13) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . D2 20. Коэффициент расхода жидкости . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . µ
21. Площадь сечения жиклёра нижней полости . . . . . . . . . . . . . . . . . . . . . . . . fж
325
22. Плотность жидкости (масла) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . γ 23. Площадь рабочей поверхности нижней полости поршня . . . . . . . . . . . . . Fк.п
24. Показатель политропы сжатия воздуха в компрессоре . . . . . . . . . . . . . . . . .пн
25. Температура окружающей среды, 0 К . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .T0
26. Степень охлаждения воздушного заряда в охладителе, град . . . . . . . . . ∆Tхол
27. Коэффициент наполнения . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ηv
28. Степень подогрева воздушного заряда при впуске, град . . . . . . . . . . . . . . ∆T
29. Исходное значение степени сжатия . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .ε0 30. Давление окружающей среды . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . p0 31. Температура остаточных газов, 0 K . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Tr
32. Элементарный химический состав топлива:
Массовая доля углерода . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . C водорода . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . H кислорода . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .O серы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . S
33. Показатель политропы сжатия рабочего тела . . . . . . . . . . . . . . . . . . . . . . . . n1
34. Угол опережения воспламенения, град . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . θ 35. Показатель характера сгорания . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . m 36. Продолжительность сгорания, град. ПКВ . . . . . . . . . . . . . . . . . . . . . . . . . . .ϕz
37. Коэффициент избытка воздуха . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . α 38. Коэффициент эффективности сгорания . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .ξ
39. Теплотворность топлива (низшая) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Hи
40. Приведенная масса иглы сливного клапана . . . . . . . . . . . . . . . . . . . . . . . . . mкл 41. Площадь рабочей поверхности иглы сливного клапана . . . . . . . . . . . . . . . . fкл 42. Предварительный натяг пружины клапана . . . . . . . . . . . . . . . . . . . . . . . . . Ро.пр 43. Площадь дополнительной рабочей поверхности иглы сливного
клапана . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . fкл.доп 44. Жёсткость пружины клапана . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . C
45. Диаметр отвода . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .dо
46. Угол конуса при вершине иглы сливного клапана, град . . . . . . . . . . . . . . . .α
47. Максимальный подъём иглы клапана . . . . . . . . . . . . . . . . . . . . . . . . . . . . . yмакс 48. Ход поршня . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . S
49. Максимальное значение степени сжатия . . . . . . . . . . . . . . . . . . . . . . . . . εмакс
50. Минимальное значение степени сжатия . . . . . . . . . . . . . . . . . . . . . . . . . . . .εмин
51. Показатель политропы расширения . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . n2 52. Коэффициент сжимаемости жидкости . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . β
Приведённая динамическая модель рабочего цикла дизеля с ПАРСС пригодна для расчёта установившихся и переходных режимов работы. При ис-
326
следовании переходного процесса (например, в условиях резкого наброса нагрузки) некоторые из исходных данных должны вводиться в виде таблиц или в виде функциональных зависимостей. К таким параметрам относятся, прежде
всего, α, Тr, Θ, ϕz, ζ.
В случае расчёта процессов сброса или наброса нагрузки на двигатель целесообразно коэффициент избытка воздуха задавать табличным способом. Для определения Тr (Тr ≈ Тг) и ϕz могут быть использованы статистические зависимости, устанавливающие их связь с коэффициентом избытка воздуха.
Примеры расчётов параметров рабочего цикла дизеля с ПАРСС по приведённой математической модели представлены в следующем разделе.
Необходимо отметить, что уравнения, составляющие динамическую модель рабочего цикла дизеля с регулируемой ε , записаны применительно к конструктивной схеме двигателя с ПАРСС, имеющего «длинную» оболочку (оболочка охватывает стержень поршня). В случае рассмотрения какой-либо другой конструктивной схемы регулирования может возникнуть необходимость изменения отдельных составляющих модели. Однако, в целом сущность рассмотренного метода от этого не изменится, так как метод базируется на основных законах механики, термо- и гидродинамики.
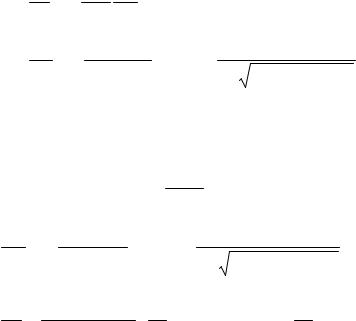
Изложенный метод описания параметров цикла обладает свойством общности: из него, например, легко выводится модель рабочего цикла для двигателя с обычным, жёстким, поршнем. Так, для описания процесса сжатия дви-
гателя с жёстким поршнем имеем систему |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
dp = − n1 p dν , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
dt |
|
|
|
ν |
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(12. 59) |
||||||||
|
|
dν |
|
|
|
ν |
с |
(ε |
−1) |
|
|
|
|
|
|
|
λ sin 2α |
|
|
|
|
. |
|||||||||||
|
|
= − |
|
|
|
|
|
|
|
|
|
ω |
|
||||||||||||||||||||
|
|
dt |
|
|
2 |
|
|
|
sinα + |
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
1 − λ |
sin |
α |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Для описания процесса сгорания |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
dν |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dp |
|
|
(k −1)qz |
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
dt |
p, |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
dt |
|
|
|
ν |
|
|
|
dt |
ν |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
dν |
|
|
|
ν |
|
(ε −1) |
|
|
|
|
|
|
|
λ sin 2α |
|
|
|
|
|
|
|
|||||||||||
|
= − |
c |
|
|
+ |
|
|
|
|
|
|
|
|
(12. 60) |
|||||||||||||||||||
|
dt |
|
|
2 |
|
|
sinα |
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
ω . |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
1 − λ |
sin |
α |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
m+1 |
|
|
|
|||
|
dx |
|
6,908(m +1) tг |
|
|
|
|
|
tг |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
exp |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
dt |
|
|
|
|
t z |
|
|
|
|
|
|
|
|
− 6,908 |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
t z |
|
|
|
|
|
|
|
t z |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для расширения
327
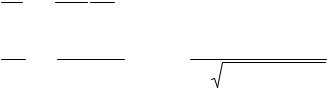
dp = − n2 p dν , |
|
|
|
|
|
|
|
|
|
||||
dt |
|
ν |
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(12.61) |
||||
dν |
|
ν |
c |
(ε −1) |
|
|
λ sin 2α |
|
|
. |
|||
= − |
|
|
ω |
|
|||||||||
dt |
|
2 |
sinα + |
|
|
2 |
|
2 |
|
|
|||
|
|
|
|
2 |
1− λ |
sin |
|
|
|
||||
|
|
|
|
|
|
|
|
α |
|
|
|||
Системы (12. 59), (12. 60), (12. 61) с помощью введения ступенчатых функций могут быть обобщенны в систему двух дифференциальных неоднородных уравнений первого порядка. Таким образом, при условии допущения об изохорности процессов смены рабочего тела может быть получена очень компактная математическая модель индикаторной диаграммы рабочего цикла.
12. 7. Характеристики двигателей с ПАРСС
Общие замечания. В предыдущем разделе было показано, что рабочий цикл дизеля с автоматическим регулированием степени сжатия описывается нелинейной системой обыкновенных дифференциальных уравнений, которая одинаково справедлива для условий работы с установившейся и переменной нагрузкой.
В дальнейшем под установившимся (стационарным, устойчивым) режимом работы понимается режим, при котором все переменные величины (например, температура жидкого рабочего тела, частота вращения коленчатого вала, давление в масляной магистрали, а также давление газообразного и жидких рабочих тел, температура газообразного рабочего тела, скорость истечения жидкости из рабочих камер поршня и т. д.), его определяющие, не меняются во времени или остаются вполне определенными периодическими функциями времени. Если параметры, характеризующие режим работы двигателя, не остаются постоянными во времени и (или) не являются периодическими функциями времени, то состояние системы не является установившимся. Такой режим работы в последующем называется нестационарным (неустановившимся, переходным).
Приведённое определение подразумевалось и ранее, когда употреблялись следующие термины: «установившийся», «неустановившийся» или «переходный» режим работы.
Рабочий цикл двигателя с ПАРСС при его работе на установившемся режиме с высокой степенью приближения можно рассматривать как рабочий цикл двигателя с обычным (жёстким) поршнем. Конечно, это справедливо лишь в том случае, когда перемещения оболочки относительно стержня поршня остаются малыми (амплитуда колебаний составляет примерно 0,1…0,15 мм). При
328
работе на установившемся режиме амплитуда колебаний должна оставаться незначительной с точки зрения обеспечения надлежащих качеств по износостойкости, надёжности и долговечности. Но эта амплитуда должна, всё же, быть достаточной для того, чтобы благодаря прокачиванию масла через полости поршня обеспечивать соответствующий теплоотвод от его поверхностей и поддерживать температуру деталей на допустимом уровне.
В таком случае расчёт рабочего цикла двигателя с ПАРСС представляет интерес лишь с точки зрения определения оптимальных величин его конструктивных и регулировочных параметров. Таких параметров, которые обеспечивали бы малые колебания оболочки поршня. В этом и состоит ценность изложенного метода расчёта.
Другое достоинство метода заключается в том, что он позволяет определять на стадии проектирования двигателя все интересующие исследователей параметры в период переходных режимов.
С этой точки зрения особый интерес представляет случай резкого (в частности, мгновенного) наброса нагрузки на двигатель. В таких условиях максимальные давление и температура газообразного рабочего тела резко возрастают. Предлагаемый метод и позволяет установить величину «всплеска» давления и температуры, а также характер их изменения в переходном процессе. Он же дает возможность рассчитать продолжительность переходного процесса, что представляет несомненный интерес и с практической точки зрения.
Поскольку оказывается возможным выявить параметры и продолжительность переходного процесса, то становится реальной возможность оценки степени эффективности тех или иных мероприятий, направленных на улучшение показателей системы автоматического регулирования степени сжатия.
Не менее важно знать протекание основных параметров системы регулирования в переходном процессе при сбросе нагрузки.
Настоящий раздел посвящён анализу особенностей рабочего цикла дизеля с ПАРСС при работе на установившихся и переходных режимах.
12. 7. 1. Нагрузочная характеристика
Нагрузочной характеристикой отображается характер изменения параметров двигателя при работе его с различными нагрузками. Но каждая из нагрузок соответствует условиям испытаний при установившемся режиме работы.
На рис. 12. 20 приведена нагрузочная характеристика дизеля 1ЧВН15/16 с ПАРСС при частоте вращения 1250 об/мин. Поршень обеспечивал возможность регулированием ε в пределах от 10 до 16.
329
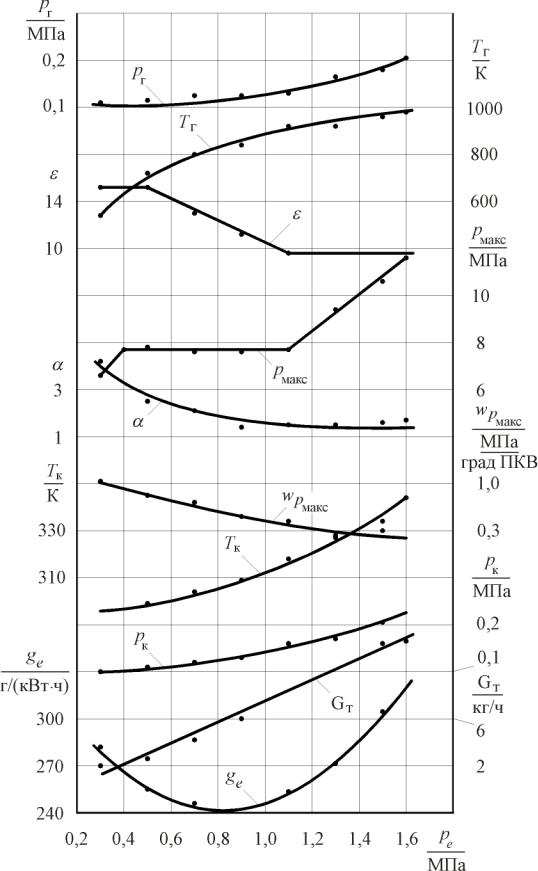
Рис. 12. 20. Изменение показателей дизеля с ПАРСС при работе по нагрузочной характеристике (п = 1250 об/мин; εмин = 10; εмакс = 16)
330
