Добавил:

DIF Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский автомобильно-дорожный государственный технический университет

Предмет:

Двигатели внутреннего сгорания

Файл:

Учебник. Двигатели внутреннего сгорания теория, моделирование и расчёт процессов / DVS_teoriy_modelir_i_raschet_processov2

.pdf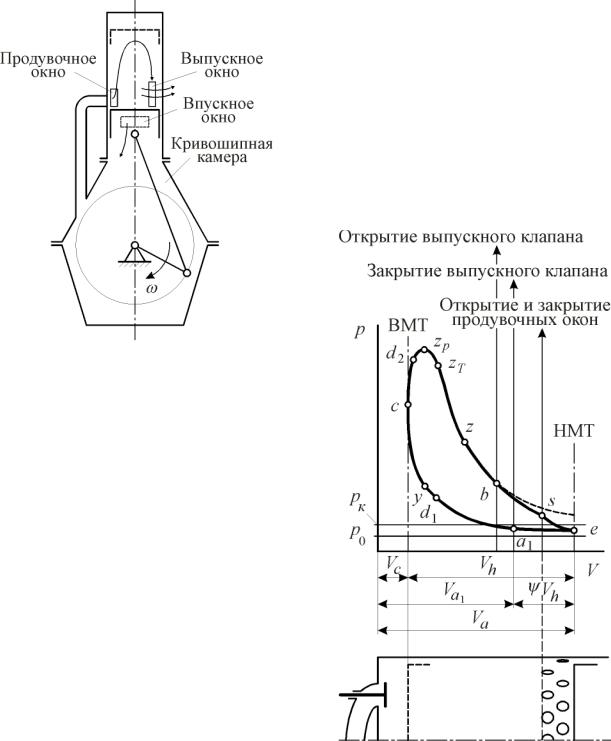

Скачиваний:

678

Добавлен:

04.06.2014

Размер:

3.28 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 1810 11 12 13 14 15 16 17 18 > Следующая >>>

продувкой

Рис. 11. 5. Индикаторная диаграмма двухтактного дизеля с прямоточно-щелевой

Кривошипно-камерная продувка

Эта схема несовершенна (рис. 11. 4), но не требует продувочного насоса. Его роль выполняет поршень с кривошипной камерой. Коэффициент остаточных газов для этой схемы продувки велик и находится в пределах 0,30…0,40. Применяется в карбюраторных, мотоциклетных, пусковых двигателях.

Рис. 11. 4. Схема кривошипнокамерной системы продувки

11. 2. Индикаторная диаграмма двухтактного дизеля с прямоточной клапанно-щелевой продувкой

Как видно из индикаторной диаграммы двухтактного двигателя (рис. 11. 5), действительное сжатие в цилиндре начинается после момента закрытия продувочных или выпускных органов, то есть, тех органов, которые закрываются последними. Обычно таковыми (в двигателях без наддува) являются выпускные органы. Обозначим через ψ от-

ношение Sпот/S, где Sпот – перемещение поршня от положения в НМТ до момен-

та закрытия продувочных (или выпускных) окон, и назовём это отношение потерянной долей хода поршня. Числен-

ные значения этого коэффициента для двигателей с разными системами продувки приведены в табл. 11. 1.

261

Численные значения потерянной доли хода поршня		Таблица 11. 1
Численные значения потерянной доли хода поршня

Вид продувки	Коэффициент ψ
Вид продувки	Контурная	Прямоточная
	Контурная	Прямоточная
Малооборотные двигатели (n = 100…500 мин–1 )	0,16…0,32	–
Высокооборотные двигатели (n = 1500…3000 мин–1)	0,38…0,42	0,18…0,22

В связи с изложенным в двухтактных двигателях различают номинальную и действительную степени сжатия.

Номинальная (геометрическая) степень сжатия ε = Va/Vc, выше, чем дей-

ствительная εд = Va1/Vc.
Действительная степень сжатия
	Va		V	a	−ψV	h
εд =	1	=		a		h	= ε − (ε −1)ψ = ε(1	−ψ) +ψ .
εд =	Vc	=			Vc		= ε − (ε −1)ψ = ε(1	−ψ) +ψ .
	Vc				Vc

Таким образом, действительная степень сжатия – это отношение объёма полости цилиндра в момент закрытия органов газораспределения, закрывающихся последними, к объёму пространства сжатия.

Номинальная степень сжатия

ε = εд −ψ .

1−ψ

Фазы процессов выпуска и продувки-наполнения

В фазах процессов выпуска и продувки-наполнения двухтактных двигателей (рис. 11. 6) без наддува (pк = 0,12…0,16 МПа) и с наддувом (pк = 0,18…0,4 МПа) введены следующие условные обозначения:

p0 – атмосферное давление;

pк – давление продувочного воздуха в продувочном ресивере; pг – давление отработавших газов в выпускном трубопроводе;

ps – давление в цилиндре в момент начала продувки (к моменту открытия продувочных окон давление в цилиндре должно быть несколько меньше, чем pк ,чтобы газы не затекали в ресивер);

pкp – критическое давление;

pa – условное давление рабочего тела в начале такта сжатия (получается экстраполированием политропы сжатия от точки а1 на линию НМТ). Его лучше вычислить через ηv, который определяется экспериментально.

На индикаторной диаграмме можно выделить следующие фазы выпуска и продувки:

b – k – s – фаза свободного выпуска. Эта фаза включает два периода,

262

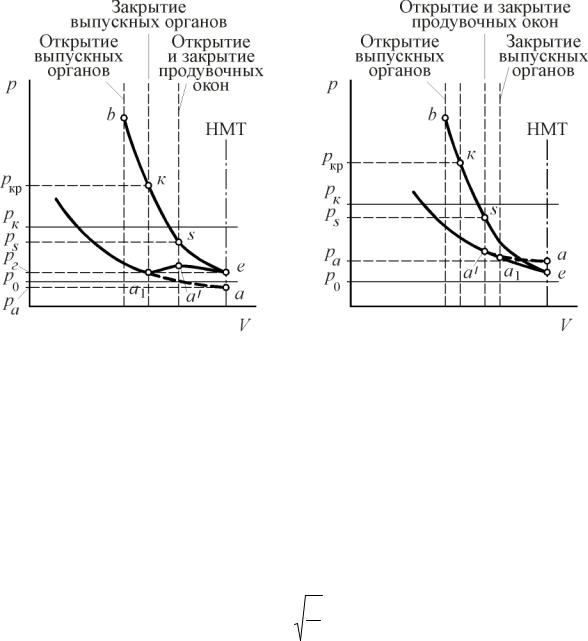
протекающих последовательно: b – k – период надкритического свободного выпуска и k – s – период подкритического свободного выпуска;

s – e – a’ –фаза продувки цилиндра. В течение этой фазы одновременно происходит наполнение цилиндра свежим зарядом и принудительная очистка цилиндра от отработавших газов;

a’ – a1 – конечная фаза процесса выпуска; при наддуве – дозарядка цилиндра (а1 – а/); a1 – y – процесс политропического сжатия (точка у – момент воспламенения – на рисунке не обозначена); a – a1 – условный участок политропического сжатия.

а) б)

Рис. 11. 6. Фазы процессов выпуска и продувки-наполнения двухтактных двигателей: а) – для двигателей без наддува; б) – для двигателей с наддувом

11. 3. Необходимое время-сечение

Уравнение необходимого времени-сечения в общем виде для фазы свободного выпуска

Секундный расход газа при истечении из отверстий определяется уравнением расхода

G = µfψ	p	, кг/с	(11. 1)
	v

где f – площадь поперечного сечения выпускных отверстий; µ – коэффициент расхода;

p и v – давление и удельный объём рабочего тела в цилиндре двигателя;

263

ψ– некоторая функция (функция расхода), имеющая различные значения для надкритического и подкритического периодов свободного выпуска: для надкритического периода (b – k) она имеет наибольшее значение и постоянна по величине, зависит только от состава (термодинамических свойств) отработавших газов, а именно:

	2	1	2k


ψ =ψмакс =		k−1	k −	1	,

k +1

где k = Сp/Сv – отношение теплоёмкостей (Ср – теплоёмкость рабочего тела при постоянном давлении, Сv – теплоёмкость при постоянном объёме).

Для подкритического периода (к – s) функция ψ зависит от отношения

давлений рг/р и изменяется по следующему закону:

k+1

ψ =

−

k −1

где p – текущее давление;

pг – давление в выпускном трубопроводе.

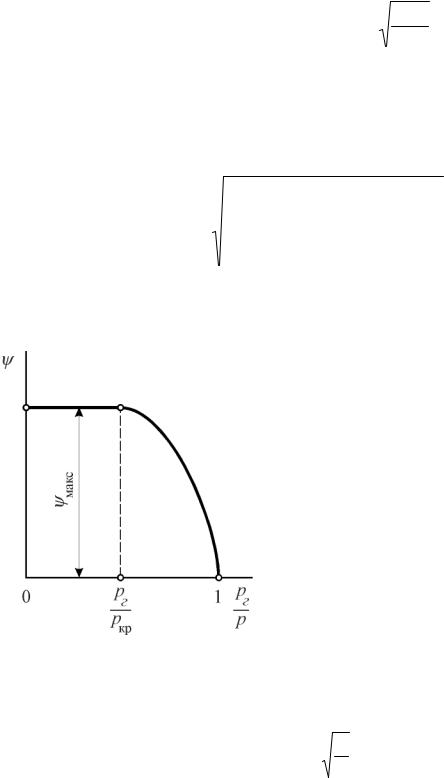
Характер протекания функции ψ поясняется графиком – рис. 11. 7.

Для среднего состава отработавших газов k ≈ 1,3; критическое отношение давлений равно

		pг		2	k		ркр
		pг		2	k+1	= 0,546 ;	ркр	=1,83.
			=
		pкp	=				рг
		pкp	k	+1			рг
		В реальных условиях работы двигате-
	ля в момент открытия выпускных органов
	(точка b индикаторной диаграммы) отноше-
	ние pb/pг значительно превышает величину
	1,83. Поэтому при свободном выпуске на-
	чальный период истечения отработавших га-
Рис. 11. 7. Характер протекания	зов всегда является надкритическим.
функции расхода		Массовый расход газа в дифферен-
функции расхода	циальной форме в соответствии с уравнени-
ем (11. 1) можно записать в виде	циальной форме в соответствии с уравнени-
ем (11. 1) можно записать в виде
dG = µfψ			pdt .					(11. 2)
			v

Примем во внимание, что

264

G = Gв − Gi ,
откуда
dG = d(Gв − Gi )= −dGi ,	(11. 3)

где G – массовое количество рабочего тела, вытекающего из цилиндра через выпускные окна за определённый отрезок времени;

Gв – массовое количество рабочего тела, находившегося в цилиндре в момент открытия выпускных органов;

Gi – количество рабочего тела в цилиндре в текущий момент времени t. Обозначим через V текущий объём рабочего тела в цилиндре. Тогда

уравнение (11. 3) примет вид		V
	dG = −d		.	(11. 4)

		v
Приравняем правые части уравнений (11. 2) и (11. 4). Получим
− d	V = µfψ	рdt .		(11. 5)
	v	v

Условимся считать процесс расширения рабочего тела политропическим, протекающим с показателем политропы m. Тогда

pvm = pbvbm ,

откуда

v = vв ppв m ,

(11. 6)

pв

vв

pв

vв

pв

Уравнение (11. 5) с учётом выражения (11. 6) можно записать в следующем виде:

	p		p			1	+		1
µfψ	p		p		2m		+	2		dt
µfψ		в								dt

	vв		pв
или
				p			1	+		1
							2	+		2m
µfψ							2			2m
µfψ	pвvb
				pв

= −

m V

vв

pв

dt = −d

m V .

pв

265

µfψ V

Поделим обе части полученного выражения на

. Тогда

pв

−

−1

pвvв

dt = −

dV +

pв

= − dV −

pв

Решим уравнение относительно fdt. Принимая V = Сonst, получим

fdt = − µm

После интегрирования

∫ fdt = −

−

−1

2m 2

pвvв ψ

pв

−

∫

(11. 7)

µm pвvв

pв

Выражение (11. 7) представляет собой уравнение необходимого време- ни-сечения в общем виде для процесса свободного выпуска рабочего тела из цилиндра. Оно пригодно также и для четырёхтактных двигателей. Его нужно привести к виду, удобному для инженерных расчетов.

Уравнение необходимого времени-сечения для надкритического периода свободного выпуска

Для надкритического периода свободного выпуска (b – k) функция рас-

хода ψ = ψмакс = Const. Имея это в виду, выражение (11. 7) легко проинтегрировать:

pкp

−

ВСчн.кр =

∫ fdt = −

∫

µm p v

макс

t =0

в в

pкp

1−m

pв

= −

µm p v

−

в в

макс

266

1−m

pг

pкp

m −1 µ

−1

макс

pв pг

m−1

pв pг

−1 .

m −1

pвvв

Ψмакс pг pкp

После подстановки выражений для рг/ркp, ψмакс и, учитывая, что рвνв =

= RгTв , получаем

m−1

tк

k m−1

∫

fdt =

k −1 2m

pв

−1 . (11. 8)

tв

m −1

k +1

R T

k −1

г в

k +1

На основе экспериментальных данных можно принять k ≈ m ≈ 1,3. Учи-

тывая, что Rг = 286,7, уравнение (11. 8) переписываем окончательно

tк

pв

0,115

∫ fdt =

0,0277

−1 .

0,932

Tв

Приближённо можно принять

V = Vв +Vкр , 2

где Vкр – объём цилиндра (соответственно и рабочего тела) в момент завершения надкритического периода истечения. Для приближённой оценки его величины может быть использовано соотношение

Vкp = ppкрв m Vв .

В некоторых источниках [16, 24] содержатся рекомендации по оценке величины V как полусуммы Vb и Vs, то есть, принимается

V = Vb +2 Vs ,

где Vs – объём цилиндра в момент открытия продувочных окон.

Давление и температура рабочего тела в момент открытия выпускных органов (рв и Tв соответственно) достаточно точно определяются тепловым расчётом. Для этого необходимо задаться величиной угла поворота коленчатого вала, при котором открываются выпускные органы.

267

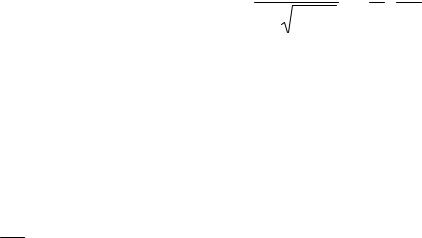
Таким образом,

tк

ВСчн.кр = ∫

	p	в
		в

fdt = F	pг		,V , µ,Tв .
	pг

tк

Анализ показывает, что ∫ fdt зависит от геометрических и термодина- o

мических параметров, от коэффициента расхода µ, численное значение которого выбирается в следующих пределах:

0,65…0,75 – для выпускных окон с острыми кромками; 0,80…0,85, если внутренние кромки окон слегка округлены.

Уравнение необходимого времени-сечения для подкритического периода свободного выпуска

На основании уравнения (11. 7) для подкритического периода истечения можно записать

−

ВСчп.кр = ∫

fdt = −

∫

tк

µm pb vв pкр

В записанном выражении подынтегральная функция является функцией

двух переменных: отношений давлений

(так как ψ =

рb

Её (подынтегральную функцию) можно привести к виду, удобному для интегрирования, или другими словами, можно преобразовать так, чтобы она стала функцией одной переменной, а именно, функцией от отношения давлений

ppг . Проведём соответствующие преобразования

−1

pb pг

После дифференцирования полученного выражения имеем

−2

= −

С учётом проведенных преобразований выражение для времени-сечения подкритического истечения запишется в виде

268

pb 1

−

pг

ВСчп.кр =

fdt = −

∫

µm pbvb p∫ ψ

pкр

tк

кр

pг

−

pг

−

∫

µm p v

b b

pг

pкр

pг −2		p
	d		=
p
		pb

p d pг =

pг

−

∫

µm pbvb

pг

кр

Точное аналитическое решение полученного

выражения невозможно

ввиду сложной зависимости подынтегральной функции от

pг

Обычно применяют графический метод отыскания численного значения интеграла, входящего в полученное выражение.

Обозначим

pг

∫

= Z .

pг

кр

Порядок отыскания Z (см. рис.11. 8) следующий (в качестве независи-

мой переменной рассматривается отношение

pг

– рассчитывается и вычерчивается функция ψ;

m+1

–рассчитывается и вычерчивается функция pг 2m ;

–строится график функции, являющейся произведением двух названных

			m+1
	p
	p	г	2m
функций ψ		г		;
функций ψ				;
	p
	p

269

Рис. 11. 8. Графический метод вычисления интеграла Z при определении необходимого временисечения для подкритического периода свободного выпуска

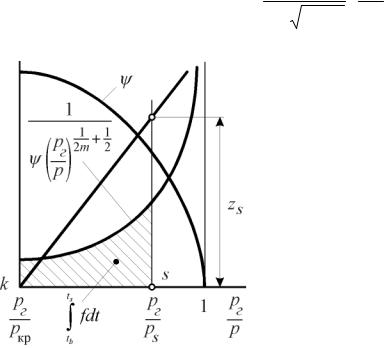
– по полученной функции вычисляется и строится обратная ей функция,

то есть,

. Площадь, ограниченная этой функцией, в заданных пре-

m+1

pг

делах интегрирования (от

до

) и определяет численное значение инте-

pкр

грала Z.

Таким образом,

−

ВСчп.кр = ∫

fdt =

Ζ.

tк

µm pbvb

Следует помнить, что при определении времени-сечения подкритического периода истечения для свободного выпуска параметры pb и vb определяются по результатам теплового расчёта, а давление в выпускной системе pг оценивается, исходя из выбранного типа системы продувки, частоты вращения вала двигателя, степени его форсирования и т. д. Величину давления в выпускной системе для безнаддувных двигателей выбирают в пределах 1,05…1,10 p0, а для двигателей с газотурбинным наддувом – в пределах 0,75…0,90 pк (p0 – давление окружающей среды, pк – давление наддува). Численное значение объёма рабочего тела V можно принять равным величине объёма рабочего тела в момент начала его подкритиченского истечения. Давление рабочего тела

в цилиндре в момент открытия продувочных окон может быть установлено, исходя из политропического характера процесса истечения, а при приближённых расчётах выбирается в пределах 1,1…1,8 pк .

Таким образом, общее время-сечение, необходимое для процесса свободного выпуска, когда свободный выпуск включает периоды надкритического и подкритического истечений, определится выражением

270

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 1810 11 12 13 14 15 16 17 18 > Следующая >>>

Соседние файлы в папке Учебник. Двигатели внутреннего сгорания теория, моделирование и расчёт процессов

#
04.06.20143.3 Mб926DVS_teoriy_modelir_i_raschet_processov1.pdf
#
04.06.20143.28 Mб678DVS_teoriy_modelir_i_raschet_processov2.pdf