6. Электр жетектеріндегі өтпелі процестер

Алдыңғы тарауларда электржетектердің тұрақталған режимдердегі қасиеттері мен сипаттамалары қарастырылады, яғни келесі шарт орындалғанда

М - М_с = 0. (6.1)

Берілген тарауда жетектің бір тұрақталған күйден екіншісіне өту кезінде болатын тұрақталмаған немесе өтпелі процестер қарастырылады. Мұнда

(6.2)

Өтпелі процестерді пайда болуының келесі себептерін атауға болады:

- М_с өзгеруі;

М өзгеруі яғни іске қосу, тежеу, реверс, жылдамдықты реттеу, жетектің қандайда бір параметрдің өзгеруі кезінде орын алатын жетектің бір сипаттамадан екіншісіне өтуі.

Өтпелі процестерді анализдеу қажеттілігінің туу себебі, көптеген маңызды механизмдердің өнімділігі өтпелі процестердің ағу жылдамдығымен анықталады; көптеген технологиялық операциялардың орындалу сапасы өтпелі процестермен анықталады; құрал-жабдықтың механикалық және электрлік асқын жүктемелігі көп жағдайларда өтпелі процестермен анықталады.

Зерттеу обьектісінде жетектің қарапайымдатылған, идеалдандырылған моделі болады.

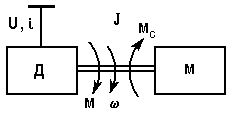
6.1 - сурет. Динамиканы зерттеуге арналған электржетек моделі.

Өтпелі процестерді меңгергенде негізгі мәселе кез-келген нақты жетектер үшін әртүрлі жағдайларда (t), M(t) және i(t) тәуелділіктерін анықтау болып табылады.

Өтпелі процестерді қарастырғанда келесі бастапқы берілістерді белгілі деп есептейміз:

• бастапқы күй: _нач, М_нач, i_нач;

• қорытынды күй: _кон, М_кон, i_кон және оған сәйкес келетін сипаттама (М);

• өтпелі процестерді тудырған фактордың уақыт бойынша өзгеру сипаты;

• жетектің параметрлері.

Тәжірибеде туатын барлық мәселелерді, оларды реттеп меңгеру мақсатында, төрт үлкен топқа бөлеміз:

1. Жетектің ең үлкен инерциялығы- механикалық инерциялық (J); электрлік инерциялық (L) өте аз немесе білінбейді. Өтпелі процесті тудыратын фактор секірмелі түрде (кенеттен) өзгереді, яғни жылдамдықтан тез. Бұл топқа жататын есептер мысалдары: жүктеменің кенеттен көбеюі немесе азаюы, іске қосу, реверс, тежелу, орамдардың индуктивтілігін ескермегенде тораптан қоректенетін асинхронды қозғалтқыштардың жылдамдығын реттеу; Ф = const, L_я = 0 болса тәуелсіз қоздырылатын тұрақты ток қозғалтқыштары үшін де солай; L_я= L_в =0 болса тізбектей немесе аралас қоздырылатын тұрақты ток қозғалтқыштары үшін де солай;

2. Жетектің ең үлкен инерциялығы-механикалық инерциялық (J); электрлік тізбектердің индуктивтілігі өте аз немесе білінбейді. Өтпелі процесті тудыратын фактор кенеттен өзгермейді, яғни оның өзгеру қарқыны  жылдамдықтың өзгеру қарқынына шамалас (әсер етуші фактордың “ақырын” өзгеруі).

Мысалдар: басқарылатын түрлендіргіш - тұрақты ток қозғалтқышы, жиілік түрлендіргіш – асинхронды қозғалтқыш (L = 0) жүйелеріндегі өтпелі процестер.

3. Механикалық және электрлік инерциялықтары шамалас; өтпелі процесс тудыратын фактор кенеттен өзгереді.

Мысалдар: ток көзі – қозғалтқыш жүйесінде; Ф = var; немесе Ф = const, бірақ L_я  0 болса тұрақты ток жетегіндегі өтпелі процестер.

4. Бірнеше инерциялық ескеріледі, өтпелі процесс тудыратын фактор кенеттен өзгермейді.

Реттеудің тұйықталған жүйелеріне қатысты осы күрделі мәселелерді біз қысқаша ғана қарастырамыз, оларға басқа пәндерде көбірек көңіл бөлінеді.

L = 0 және әсер етуші фактордың “тез” өзгергендігі өтпелі процестер

Бірінші топқа жататын барлық өтпелі процестер жылдамдықтың механикалық теңдеуіне бағынатындығы анық:

, (6.3)

(t) және M(t) тәуелділіктері бастапқы беріліс шарттарына сәйкес осы теңдеуді есептеу арқылы алынады.

Жетектің нақты ерекшеліктері M() және M_с() тәуелділіктері түрінде көрінеді

а) M = const, M_с = const

Бірінші топтағы есептерін қарастыруда өтпелі процесте M = const және M_с = const болған кездегі қарапайым жағдайдан бастайды.

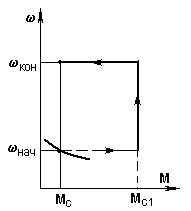
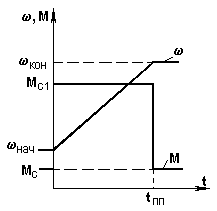
а) б)

6.2-сурет. М = const және M_c = const болған кездегі механикалық сипаттамалар (а) және уақыт тәуелділіктері (б).

Жетек (6.1-сурет) белгілі бір сипаттаманың _бас, М_бас = М_с нүктесінде (6.2-сурет) жұмыс істейді және t = 0 уақыт моментінде 6.2-суретте қалың сызықпен көрсетілген жаңа сипаттамаға кенеттен ауыстырылған.

(6.1) теңдеу бұл жағдайда дифференциалдық теңдеу болады және оның шешімі келесі түрде болады:

,

С - интегралдау тұрақтысын бастапқы шарттан анықтаймыз, егер t = 0,

 =_бас; болса, онда _бас. = С.

Яғни,

(6.4)

Бұл шешім _бас <  < _соң, интервалында әсер етеді, себебі шарт бойынша  = _соң болғанда, (М) функциясы сынады. Бұл М =М₁.

Өтпелі процесс графиктері уақыт t_ө.п. (6.2) теңдеуге  = _соң қойып және t-ға байланысты есептеу арқылы анықтауға болады.

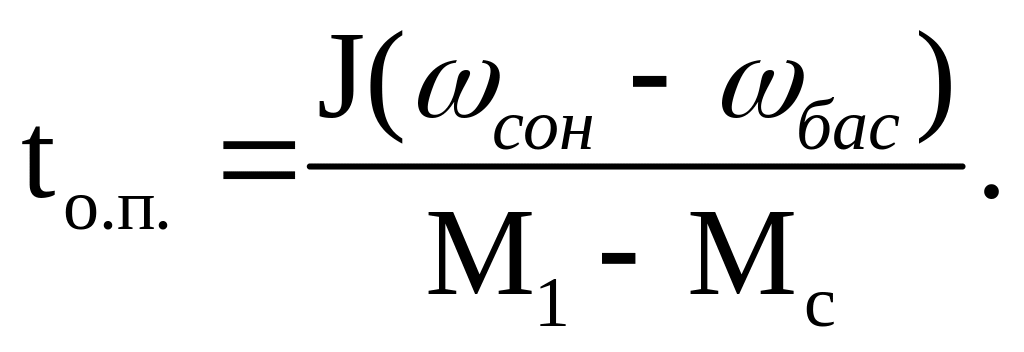(6.5)

Осы шешімді, сонымен қатар (6.1) теңдеуін dt-ға қатысты есептеп және нақты бір интегралды алып анықтауға болады:

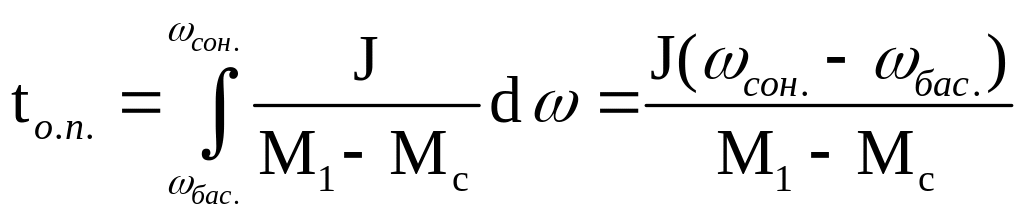
Қарастырылған қарапайым жағдайдың практикалық мағынасы өте зор, себебі өтпелі процестің уақыты мен сипатын бағалау мақсатында осы жағдайға көптеген нақты есептер келтірілуі мүмкін.

Мысалы t_п іске қосу уақытын бағалау және белгілі М_с және J механикалық сипаттамалары бар қысқа тұйықталған асинхронды қозғалтқыштың іске қосу өтпелі процесінің графигін тұрғызу.

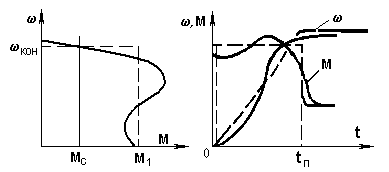
6.3-сурет. Асинхронды қозғалтқыштың механикалық сипаттамалары (а) және іске қосқандағы (t) және M(t) өтпелі процесс графиктері.

t_п белгілі болса, өтпелі процесс графигіне жақын графиктер тұрғызуға болады (6.3 б- суреттегі үздік сызық). Бұл графиктердің нақты графиктерден (үздіксіз сызық), айырмашылығы болады, бірақ көптеген жағдайларда алынған баға тиімді болады.

б) М_с = const, M, -ға сызықты тәуелді,  < 0.

Қозғалтқыштың және механизмнің сипаттамалары 6.4-суретте көрсетілгендей болсын.

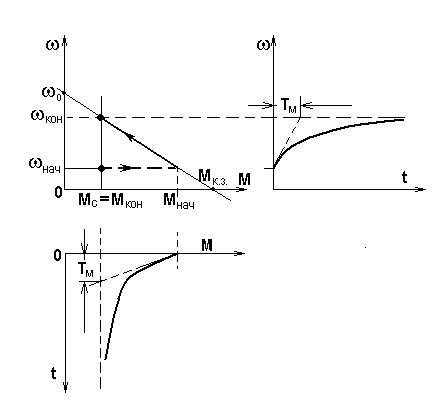
6.4-сурет. (t) сызықты тәуелділігінде механикалық сипаттамалар және (t) , M(t) өтпелі процестердің графиктері.

Қатаңдығы теріс қозғалтқыштың сызықтық механикалық сипаттама теңдеуі келесі түрде жазылуы мүмкін

(6.6)

немесе

(6.7)

мұнда - механикалық сипаттама қатаңдығы; сызықтық сипаттама үшін .

(6.5) теңдеуін (6.1) теңдеуіне қойып, қарапайым түрлендірулерден кейін алатынымыз:

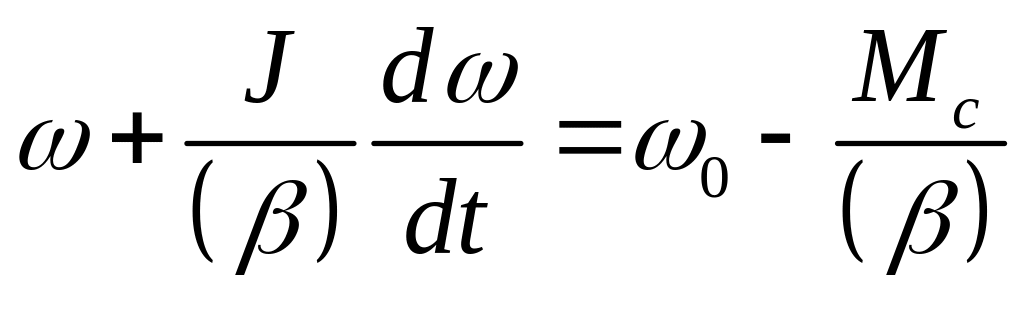
(6.4) сәйкес оң жағындағы өрнек _кон білдіреді. Туынды алдындағы коэффициентті Т_М арқылы белгілейміз.

(6.8)

Енді (6.1) теңдеуге орнына оның (6.4) алынған мәнін қоямыз:

немесе жоғарыда қабылданған белгілеулерді қолданып, алатынымыз:

(6.9)

Сонымен, қарастырылып отырған өтпелі процесте жылдамдық үшін де, момент үшін де келесі түрдегі теңдеу аламыз

, (6.10)

яғни, оң жағы тұрақты сызықтық біркелкі емес дифференциалдық теңдеу.

Коэффициент:

(6.11)

Электрмеханикалық уақыт тұрақтысы деп аталады.

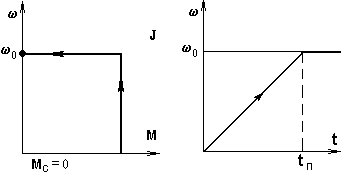
6.5-сурет. Т_М уақыт тұрақтысын анықтау.

Бұл шаманың мәнін анықтау үшін 6.5-суретте көрсетілген сипаттамаға ие шартты жетекті қарастырайық. Осындай жетектің жылдамдық алу уақытын (6.3) бойынша анықтап,

оның Т_м сияқты сипатталатынын көреміз. Сондықтан, электрмеханикалық уақыт тұрақтысы Т_м электр жетектің жылдамдығы қысқа тұйықталу моменті әсерінен бос жүрісте  = ₀ дейін жететін уақытты көрсетеді. Кейбір жеке жағдайларда Т_м-ді жетектің параметрлері арқылы көрсеткен ыңғайлы. Тұрақты ток қозғалтқышы үшін сипаттама қатаңдығын келесідей көрсетуге болады:

Бұл өрнекті (6.9) теңдеуіне қойсақ:

(6.12)

(6.8) теңдеуінің оң жағы өтпелі процесс аяқталғандағы тұрақталған шаманы көрсетеді:

x = x_cв + х_пр = Ае^pt + х_соң.,

мұнда: p – сипаттамалық теңдеудің түбірі.

1 + pТ_м = 0

яғни,

А – бастапқы шарттан анықталатын тұрақты

t = 0, x = x_бас.,

яғни: А = х_бас - х_соң.

Сонымен,

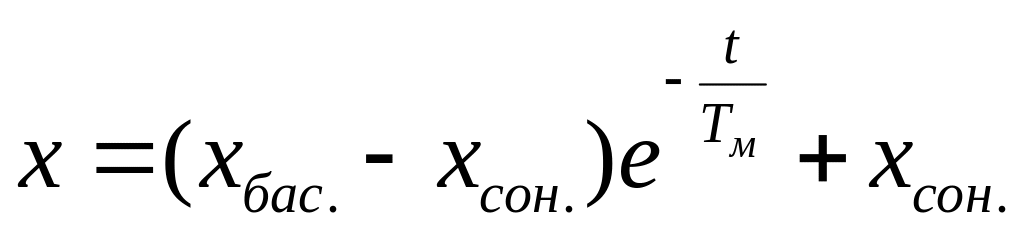(6.13)

яғни, жылдамдық пен момент өтпелі процесте бастапқы мәннен соңғы мәнге дейін экспоненциалды заң бойынша өзгереді.

Экспонентаның негізгі қасиеттері бойынша:

1. Кез-келген нүктедегі жанама тұрақталған күй сызығында Т_м тең бөлігін қияды.

2. t = Т_м уақытында шаманың өзгеруі толық өзгерістің 0,632 бөлігін құрайды.

3. t = 3Т_м өзгеру толық өзгерудің 0,95 бөлігін құрайды. Әрі қарай біз процесс t = 3Т_м уақытысында тұрақталады деп есептейміз

1-Мысал. Механикалық сипаттамасы жұмыс учаскесінде сызықты асинхронды қозғалтқыштың жүктемесі М_с1 мәнінен М_с2 мәніне күрт өскенде өтпелі процесті есептеу (6.6-сурет).

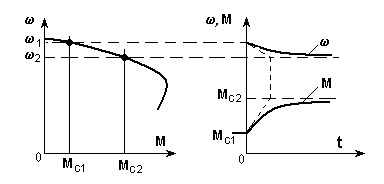
6.6-сурет. Жүктеменің күрт өсуіндегі өтпелі процесс.

Т_м есептейміз:

 және М бастапқы және қорытынды мәндерін анықтаймыз:

_бас. = ₁, _сон. = ₂;

М_бас. = М_с1, М_сон. = М_с2

(6.10) бойынша өтпелі процесс теңдеуін жазамыз:

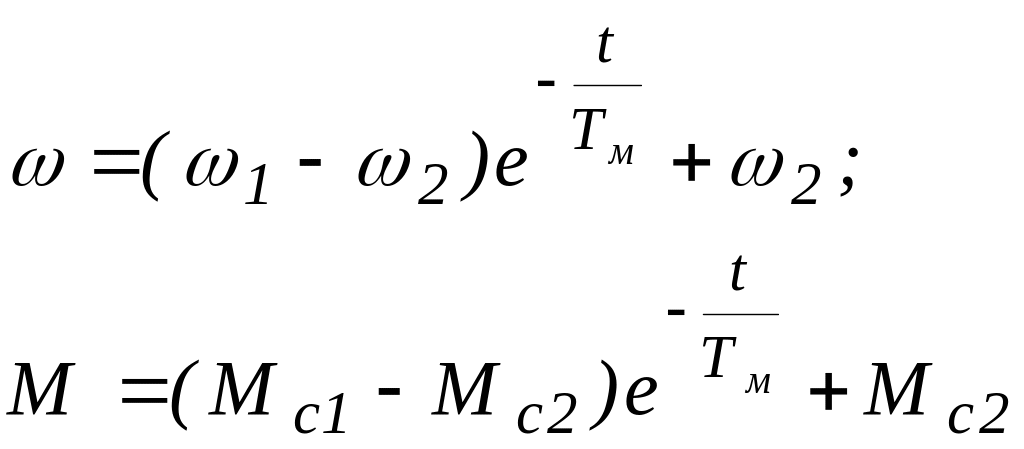
және графиктер тұрғызамыз (6.6-сурет).

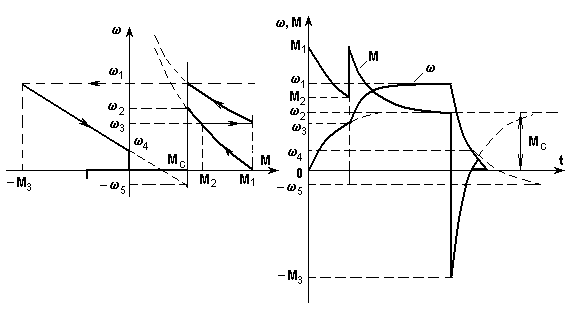
2-Мысал. Тізбектей қоздырылатын тұрақты ток қозғалтқышының іске қосу реостатының бір сатысымен іске қосылуы және динамикалық тежелуі кезіндегі өтпелі процесті есептеу; М_с – реактивті.

а) б)

6.7-сурет. Тізбектей қоздырылатын қозғалтқыштың реостаттық іске қосу және динамикалық тежеу кезіндегі механикалық сипаттамалары (а) және өтпелі процесс қисықтары (б).

Алдымен іске қосу диаграммасын тұрғызамыз (6.7а). Егер сипаттаманың жұмыс бөлігі түзуге жақын болса, онда есепті аналитикалық жолмен есептеуге болады. Берілген жағдайда механикалық сипаттаманың үзілген жерлері (₃, ₁) және сынған (₄) бөліктері бар, сондықтан өтпелі процесті бірнеше учаскеге бөлу қажет, ал әр учаскеде (М) және (М_с) функциялары сызықты болуы керек.

Біздің жағдайда төрт учаскеге бөлеміз:

I - 0<  < ₃ (реостаттық сипаттамада іске қосу);

II - ₃ <  < ₁ (табиғи сипаттамада іске қосу);

III - ₁ >  > ₄ (өздігінен қоздырылып тежеу);

IV - ₄ <  < 0 (М_с әсерінен тежелу).

Бірінші үш учаскеге қатысты (6.10) теңдеу қолданыла алады, себебі бұл учаскелер шегінде М() – сызықты функциялар; IV учаскеге, М = 0 және М_с= const, (6.2) теңдеуді қолданған жөн.

Біз қолданатын (6.10) және (6.2) теңдеулерінде уақыт санағы өтпелі процесті тудырған өзгерістер болған t=0 моментінен басталады. Сондықтан, бұл есепті кезең бойынша есептегенде уақыт санағын әр кезеңнің өз басынан бастау қажет. Өтпелі процестің толық уақыты барлық кезеңдер уақытының қосындысы ретінде анықталады.

(6.10) және (6.2) теңдеулерін қолдану үшін, ондағы шамалардың бастапқы және соңғы мәндерімен уақыт тұрақтыларын анықтап алған жөн. Қарастырылып отырған есеп үшін бастапқы және соңғы мәндер 6.1-кестеде көрсетілген.

6.1 – кесте

кезең№	бас.	сон.	Мбас.	Мсон.	Тм	Ескертулер
I	0	2	М1	Мс		(6.10) теңдеу
II	3	1	М1	Мс		(6.10) теңдеу
III	1	-5	-М3	Мс		(6.10) теңдеу
IV	4	0	0	0	-	(6.2) теңдеу Процесс  = 0 болғанда аяқталады, себебі Мс - реактивті

6.1-кестедегі берілгендер әр кезең үшін теңдеулерді жазуға және графиктерін тұрғызуға (6.7б-сурет) мүмкіндік береді.

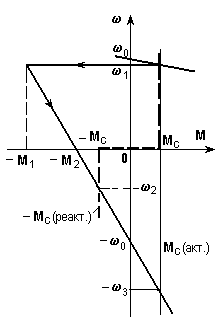
3-Мысал. U = const тораптан қоректенетін тәуелсіз қоздырылатын тұрақты ток қозғалтқышының реверсінің өтпелі процесс қисығын есептеу және тұрғызу, М_с активті және реактивті сипатта.

а) б

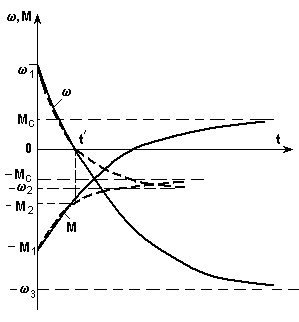
6.8-сурет. Электр жетегінің реверс кезіндегі механикалық сипаттамалары (а) және өтпелі процесс қисықтары (б).

Есептеуді (М) графиктерін тұрғызудан бастаймыз. Реактивті М_с графигі үзік сызықпен көрсетілген. Алдымен М_с активті болған жағдайды қарастырайық. Өтпелі процесс бір кезеңде жүреді, ал оның (6.10) өрнектен алынған теңдеулері келесі түрде болады:

мұнда:

Сәйкес графиктер 6.8 б-суретте үздісіз сызықпен көрсетілген.

М_с реактивті болғанда,  = 0 кезінде таңба өзгереді және екі кезеңде қарастырылады: І - =₁ мәнінен =0 дейін және II - =0 мәнінен  =-₂ мәнге дейін. I-ші кезеңде теңдеулер алдында алынған теңдеулерден айырмашылығы жоқ. Бұл кезеңде М_с-ның реактивтік сипаты көрінбейді және бірінші жағдайдағы сияқты жетектің тежелуіне әкеледі.

ІІ-ші кезеңде М_с таңбасы өзгереді және М_с жетектің қарама-қарсы бағытта жылдамдық алуында тежеулік әсер етеді. Бұл кезеңде теңдеу келесі түрге ие болады:

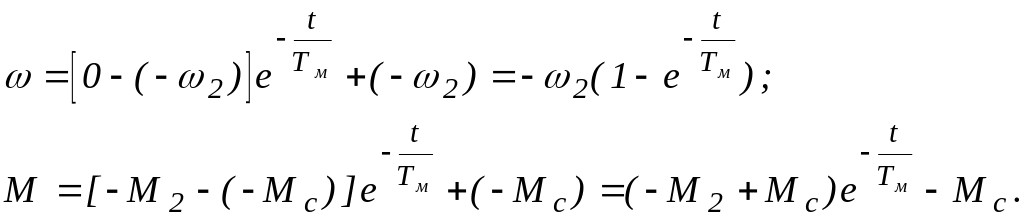
М_с реактивті болған кездегі өтпелі процесс графиктері 6.8,б-суретте пунктир сызықпен көрсетілген. t уақыт моментінде қисықтар сынады, процесс темпі баяулайды, бұл М_с таңбасының өзгеру себебінен динамикалық моменттің секірмелі түрде азаюына байланысты.

Егер i(t) тәуелділігін анықтау қажет болса, келесі қатынасты қолдануға болады:

в) М_с = const, M сызықты түрде  -дан тәуелді,  > 0

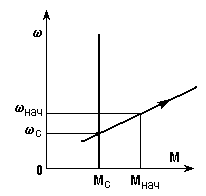
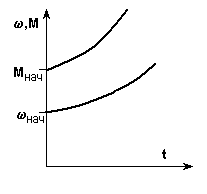
Жоғарыда қарастырылған өтпелі процестер,  <0 болғанда, тұрақталған режимнің тұрақты нүктесіне _сон., М_сон. сәйкес келеді, яғни  және М өзгере отырып, осы нүктеге ұмтылды. Сонымен қатар, кейде тұрақталған режимнің тұрақсыз нүктесіне сәйкес келетін  >0 болғанда өтпелі процесті есептеу қажеттілігі туады (6.9а-сурет).

а) б)

6.9-сурет.  > 0 болғандағы механикалық сипаттамалар (а) және өтпелі процесс қисықтары.

Бұл жағдайда жетектің механикалық сипаттамасының теңдеуі келесі түрде жазылады:

немесе

Бұл өрнектерді (6.1) теңдеуге қойсақ, кейбір түрлендірулерден кейін келесі теңдеуді аламыз:

(6.14)

мұнда: х - жылдамдық немесе момент;

х_с- тұрақталған режим нүктесіне сәйкес келетін жылдамдық немесе момент.

(6.8) теңдеумен салыстырғанда бұл теңдеуде туынды алдындағы таңба өзгерді, оң бөлігінде айнымалының соңғы мән мағынасы жоқ х_с бар. (6.11) теңдеуін бөлінетін айнымалылары бар теңдеу ретінде есептейміз; осы әдіспен (6.8) теңдеуді де есептеуге болады:

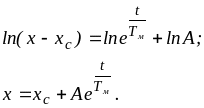
Бастапқы шарттарды: t = 0, x = x_бас. пайдаланып, келесіні аламыз:

х = (х_бас. - х_с) (6.15)

(6.12) сәйкес келетін (t) және М(t) графиктері 6.9б-суретте көрсетілген.