1. Обернених сантиметрах

2. барнах

3. Фермі

4. Кюрі

5. Греях

721.

Теор. Мех. І осн. Механіки суц. Середовищ

Частинка рухається по колу радіуса R зі сталою швидкістю v. Радіус кривини

траєкторії дорівнює

(1). R

(2). R+v²/g

(3). R+v²/2g

(4). R/2

(5). правильна відповідь відсутня

722.

Частинка рухається по колу радіуса R зі сталим прискоренням a. Радіус кривини

траєкторії дорівнює

(1). R

(2). 0

(3). R+a/2g

(4). R/2128

(5). правильна відповідь відсутня

723.

Частинка рухається по прямій зі сталим прискоренням a. Радіус кривини траєкторії

дорівнює

(1). 0

(2). -a/2g

(3). a/2g

(4). a/g

(5). правильна відповідь відсутня

724.

Частинка рухається по прямій зі сталою швидкістю v. Радіус кривини траєкторії

дорівнює

(1). 0

(2). -v²/2g

(3). v²/2g

(4). v²/g

(5). правильна відповідь відсутня

725.

Частинка рухається по еліпсу зі сталою швидкістю v. Велика та мала півосі еліпса

рівні a та b відповідно. Радіус кривини траєкторії дорівнює

(1). 0

(2). -v²/2g

(3). v²/2g

(4). v²/g

(5). правильна відповідь відсутня

726.

Частинка рухається по прямій зі сталим прискоренням a. Радіус кривини траєкторії

дорівнює

(1). 0

(2). a+b

(3). a-b

(4). (a² + b²)^1/2

(5). правильна відповідь відсутня

727.

(1). 1

(2). 2

(3). 0

(4). t

Частинка рухається за законом x=cos t, y=sin t. Модуль її швидкості рівний

(5). правильна відповідь відсутня

728.

(1). 1

(2). 0

(3). 2

(4). t

Частинка рухається за законом x=cos t, y=sin t. Модуль її прискорення рівний

(5). правильна відповідь відсутня

729.

(1). 1

(2). 2

(3). 0

(4). t

Частинка рухається за законом x=cos t, y=2sin t. Модуль її швидкості рівний

(5). правильна відповідь відсутня

730.

(1). 1

(2). 0

(3). 1/t

(4). t

Частинка рухається за законом x=cos t, y=2sin t. Модуль її прискорення рівний

(5). правильна відповідь відсутня

731.

Частинка рухається за законом x=3sin t , y=4sin t. Модуль її швидкості рівний

(1). |cos t|

(2). 5|cos t|

(3). 7|sin t|

(4). 5|sin t|

(5). правильна відповідь відсутня

732.

Частинка рухається за законом x=3sin t, y=4sin t. Модуль її прискорення рівний

(1). |cos t|

(2). 5|cos t|

(3). 7|sin t|

(4). 5|sin t|

(5). правильна відповідь відсутня

733.

(1). |t|

Частинка рухається за законом x=3t, y=4t. Модуль її прискорення рівний

(2). 5| t|

(3). 7| t|

(4). 0

(5). правильна відповідь відсутня

734.

(1). | t|

Частинка рухається за законом x=3t, y=4t. Модуль її швидкості рівний

(2). 5| t|

(3). 5

(4). 1

(5). правильна відповідь відсутня

735.

Частинка рухається за законом x=3sh t, y=4sh t. Модуль її прискорення рівний

(1). |ch t|

(2). 5|sh t|

(3). 7|sh t|

(4). 5|ch t|

(5). правильна відповідь відсутня

736.

Частинка рухається за законом x=3ch t, y=4ch t. Модуль її швидкості рівний

(1). |ch t|

(2). 5|ch t|

(3). 7|sh t|

(4). 5|sh t|

(5). правильна відповідь відсутня

737.

Виберіть набір величин, які є інтегралами руху для замкненої механічної системи

(1). енергія та імпульс

(2). енергія та момент імпульсу

(3). імпульс, момент імпульсу та енергія (4). енергія

(5). правильна відповідь відсутня

738.

Консервативною силою називається

(1). сила тертя

(2). будь-яка диссипативна сила

(3). така сила, для якої циркуляція вздовж довільного замкненого контура рівна нулю

(4). така сила, для якої циркуляція вздовж довільного замкненого контура відмінна від нуля (5). правильна відповідь відсутня

739.

На частинку масою m=1 діє сила F=a (a=const). У момент часу t=0, частинка

перебувала у точці з координатою x=0, а її швидкість рівна v=1. Знайдіть рівняння руху частинки під дією сили F та виберіть варіант правильної відповіді

(1). x(t)=at²+t+1

(2). x(t)=at²+t-1

(3). x(t)=at²/2+t

(4). x(t)=at²/2

(5). правильна відповідь відсутня

740.

На частинку масою m=1 діє сила F=t. У момент часу t=0, частинка перебувала у точці

з координатою x=0, а її швидкість рівна v=-1. Знайдіть рівняння руху частинки під дією сили F та виберіть варіант правильної відповіді

(1). x(t)=t³/6+t

(2). x(t)=t³6-t

(3). x(t)=t³/3+t

(4). x(t)=t³/3-1

(5). правильна відповідь відсутня

741.

На частинку масою m=1 діє сила F=cos t. У момент часу t=0, частинка перебувала у

точці з координатою x=0, а її швидкість рівна v=0. Знайдіть рівняння руху частинки під дією сили F та виберіть варіант правильної відповіді

(1). x(t)=cos t-1

(2). x(t)=-cos t-1

(3). x(t)=sin t+1

(4). x(t)=-cos t+1

(5). правильна відповідь відсутня

742.

На частинку масою m=1 діє сила F=sin t. У момент часу t=0, частинка перебувала у

точці з координатою x=0, а її швидкість рівна v=1. Знайдіть рівняння руху частинки під дією сили F та виберіть варіант правильної відповіді

(1). x(t)=cos t-t

(2). x(t)=-sin t-t

(3). x(t)=-sin t+2t

(4). x(t)=-cos t+2t

(5). правильна відповідь відсутня

743.

На частинку масою m=1 діє сила F=sin 2t+1. У момент часу t=0, частинка перебувала у

точці з координатою x=0, а її швидкість рівна v=1/2. Знайдіть рівняння руху частинки під дією сили F та виберіть варіант правильної відповіді

(1). x(t)=1/2 (-1/2 sin 2t+t²-t)

(2). x(t)=1/2 (-1/2 sin 2t+t²-1) (3). x(t)=1/2 (-1/2 sin 2t+t²+t) (4). x(t)=1/2 (-1/2 cos 2t+t²-1)

(5). правильна відповідь відсутня

744.

На частинку масою m=1 діє сила F=cos 2t-1. У момент часу t=0, частинка перебувала у

точці з координатою x=0, а її швидкість рівна v=1/2. Знайдіть рівняння руху частинки під дією сили F та виберіть варіант правильної відповіді

(1). x(t)=1/2 (-1/2 cos 2t+t²-t)

(2). x(t)=1/2 (-1/2 cos 2t-t²-1) (3). x(t)=1/2 (-1/2 sin 2t+t²+t) (4). x(t)=1/2 (-1/2 cos 2t-t²+t)

(5). правильна відповідь відсутня

745.

На частинку масою m=1 діє сила F=2sin t-1. У момент часу t=0, частинка перебувала у

точці з координатою x=0, а її швидкість рівна v=-2. Знайдіть рівняння руху частинки під дією сили F та виберіть варіант правильної відповіді

(1). x(t)=-2cos t-t²

(2). x(t)=-2sin t-t²/2

(3). x(t)=-2sin t+t²+t

(4). x(t)=-2sin t+t²-t

(5). правильна відповідь відсутня

746.

На частинку масою m=1 діє сила F=2cos t+2. У момент часу t=0, частинка перебувала

у точці з координатою x=0, а її швидкість рівна v=0. Знайдіть рівняння руху частинки під дією сили F та виберіть варіант правильної відповіді

(1). x(t)=-2cos t+t²+2 (2). x(t)=-2cos t t-t²/2 (3). x(t)=-2cos t+t²+t+2

(4). x(t)=-2cost t+t²-t+2

(5). правильна відповідь відсутня

747.

На частинку масою m=1 діє сила F=2(t+1). У момент часу t=0, частинка перебувала у

точці з координатою x=0, а її швидкість рівна v=0. Знайдіть рівняння руху частинки під дією сили F та виберіть варіант правильної відповіді

(1). x(t)=t³/6+t²

(2). x(t)=t³3+t²

(3). x(t)=t³/3+t

(4). x(t)=-t³/3-t³

(5). правильна відповідь відсутня

748.

Знайдіть закон руху частинки масою m=1 у потенціальному полі U=x² та виберіть

варіант правильної відповіді

(1). x=±E^1/2 sin (√2 t+φ) (2). x=±E^1/2 sin²(√2 t+φ) (3). x=±E^1/2 sin (√2 t+φ)+t (4). x=±E^1/2 cos (√2 t+φ)+t

(5). правильна відповідь відсутня

749.

Знайдіть закон руху частинки масою m=1 у потенціальному полі U=x²/2 та виберіть

варіант правильної відповіді

(1). x=±E^1/2 sin (√2 t+φ) (2). x=±E^1/2 sin²(√2 t+φ) (3). x=±(2E)^1/2 sin (t+φ) (4). x=±E^1/2 cos (√2 t+φ)

(5). правильна відповідь відсутня

750.

Знайдіть закон руху частинки масою m=1 у потенціальному полі U=2x² +4 та виберіть

варіант правильної відповіді

(1). x=±((E-4)/2)^1/2 sin (2 t+φ)

(2). x=±(E-4)^1/2 cos (√2 t+φ) (3). x=±(E/2)^1/2 sin (2t+φ) (4). x=±(E/8)^1/2 cos (4 t+φ)

(5). правильна відповідь відсутня

751.

Знайдіть закон руху частинки масою m=1 у потенціальному полі U=2x та виберіть

варіант правильної відповіді

(1). t=-1/2 (2E-4x)^1/2 +φ (2). t=1/2 (2E-2x)^1/2 +φ (3). t=- (2E+4x)^1/2 +φ (4). t=-2 (2E+2x)^1/2 +φ

(5). правильна відповідь відсутня

752.

Знайдіть закон руху частинки масою m=1 у потенціальному полі U=x-5 та виберіть

варіант правильної відповіді

(1). t=-1/5 (10E-4x)^1/2 +φ (2). t=-1/5 (2E+10-2x)^1/2+φ (3). t=- (2E+10-2x)^1/2 +φ (4). t=- (2E+10x)^1/2 +φ

(5). правильна відповідь відсутня

753.

Для лаґранжіана L = x ² — x знайдіть рівняння руху і вкажіть варіант правильної

відповіді.

(1). x” + 1 = 0

(2). 2x” — 1 = 0

(3). 2x” + 1 = 0

(4). x” + x = 0

(5). правильна відповідь відсутня

754.

Для лаґранжіана L = x ² + x² знайдіть рівняння руху і вкажіть варіант правильної

відповіді.

(1). 2x” — 1 = 0

(2). 2x” + x = 0

(3). x” — x = 0

(4). x” + x = 0

(5). правильна відповідь відсутня

755.

Для лаґранжіана L = ^x

— x² знайдіть рівняння руху і вкажіть варіант правильної

2

2

відповіді.

(1). 2x” — x = 0

(2). x” + 2x = 0

(3). x” — 2x = 0

(4). x” + x = 0

(5). правильна відповідь відсутня

756.

Для лаґранжіана L = x ² + x³ + 1 знайдіть рівняння руху і вкажіть варіант правильної

відповіді.

(1). 2x” — x² = 0

(2). 2x” + x² = 0

2

(3). x” — ^3x = 0

2

(4). x” + 3x² = 0

(5). правильна відповідь відсутня

757.

Для лаґранжіана L = ^x

— x² — 2xx знайдіть рівняння руху і вкажіть варіант

2

2

правильної відповіді.

(1). x” — 2x = 0

(2). 2x^” + x = 0 (3). x” — 2x — 2x = 0 (4). x” + 2x = 0

(5). правильна відповідь відсутня

758.

Для лаґранжіана L = ^x

+ xx знайдіть рівняння руху і вкажіть варіант правильної

2

2

відповіді.

(1). x” — 2x = 0

(2). x” = 0

(3). x” + x = 0

(4). x” + x = 0

(5). правильна відповідь відсутня

759.

Для лаґранжіана L = ^x

— 2xx + t знайдіть рівняння руху і вкажіть варіант правильної

2

2

відповіді.

(1). x” — 2x — t = 0

(2). x” — t = 0

(3). x” + x = 0

(4). x” = 0

(5). правильна відповідь відсутня

760.

Для лаґранжіана L =

⁽x +e^x)2 2

_{— x}2

2

знайдіть рівняння руху і вкажіть варіант правильної

відповіді.

(1). x” — e^2x + x = 0

(2). x” — e^2x — t = 0

(3). x” — e^2x — x = 0

(4). x” = 0

(5). правильна відповідь відсутня

761.

Для лаґранжіана L =

⁽x +e^x)2 2

_{— x}2

2

знайдіть рівняння руху і вкажіть варіант правильної

відповіді.

(1). x” — e^2x — x = 0

(2). x” — e^2x — t = 0

(3). x” — e^2x + x = 0

(4). x” = 0

(5). правильна відповідь відсутня

762.

Для лаґранжіана L =

⁽x —sin(2x)⁾² 2

— x знайдіть рівняння руху і вкажіть варіант

правильної відповіді.

(1). x” — sin⁽4x⁾ — x = 0

(2). x” — sin⁽2x⁾ + x = 0

(3). x” — sin⁽4x⁾ + 1 = 0

(4). x” — sin⁽4x⁾ — 1 = 0

(5). x” — sin⁽4x⁾ — 1 = 0

763.

Лаґранжіан вільної частинки рівний

(1). mv²/2 + U(x)

(2). mv²/2

(3). mv

(4). p²/2m + U(x)

(5). правильна відповідь відсутня

764.

Лагранжіан гармонічного осцилятора рівний.

2

(1) L = ^mx

2

(2). L = ^mx

2

2

(3). L = ^p

2m

• kx

2

2

_— kx

2

• 2

  kx

2

2

(4). L = ^mx

2

2

(5). L = ^mx

2

— kx³

765.

Лаґранжіан L виражається через кінетичну T та потенціальну U енерґії так

(1). L=T+U

(2). L=T-U

(3). L=(T+U)/2

(4). L=T/2+U

(5). правильна відповідь відсутня

766.

Для лаґранжіана L = ^x

— x знайдіть гамільтоніан та виберіть варіант правильної

2

2

відповіді

(1). H=p²-x

(2). H=p²+x

(3). H=p²/2+x

(4). H=p²/2-x

(5). правильна відповідь відсутня

767.

Для лаґранжіана L = ^x

+ 3x знайдіть гамільтоніан та виберіть варіант правильної

2

2

відповіді

(1). H=p²/2-3x

(2). H=p²/2+3x

(3). H=p²/2+x

(4). H=p²/2-x

(5). правильна відповідь відсутня

768.

Для лаґранжіана L = ^{x x}

знайдіть гамільтоніан та виберіть варіант правильної

2

2

2 2

відповіді

(1). H=p²/2-x²

(2). H=p²/2+x²/2

(3). H=p²/2+x²

(4). H=p²/2-x²/2

(5). правильна відповідь відсутня

769.

Для лаґранжіана L = ^x + ^x

знайдіть гамільтоніан та виберіть варіант правильної

2

2

2 2

відповіді

(1). H=p²/2-2x²

(2). H=p²/2+x²/2

(3). H=p²/2+2x²

(4). H=p²/2-x²/2

(5). правильна відповідь відсутня

770.

Для лаґранжіана L = ^x

— xx знайдіть гамільтоніан та виберіть варіант правильної

2

2

відповіді

(1). H=p²/2-x²/2

(2). H=p²/2+x²/2

(3). H=1/2 (p+x)2

(4). H=1/2 (p-x)²

(5). правильна відповідь відсутня

771.

Для лаґранжіана L = ^x

+ xx знайдіть гамільтоніан та виберіть варіант правильної

2

2

відповіді

(1). H=p²/2-x²/2

(2). H=p²/2+x²/2

(3). H=1/2 (p+x)2

(4). H=1/2 (p-x)2

(5). правильна відповідь відсутня

772.

Для лаґранжіана L = ^x

— xx — ^x

знайдіть гамільтоніан та виберіть варіант правильної

2

2

2 2

відповіді

(1). H=p²/2-x²/2

(2). H=p²/2+x²/2

(3). H=1/2 (p-x)2+x²/2

(4). H=1/2 (p+x)2-x²/2

(5). правильна відповідь відсутня

773.

Для лаґранжіана L = ^x

— xx + ^x

знайдіть гамільтоніан та виберіть варіант

2

2

2 2

правильної відповіді

(1). H=p²/2-x²/2

(2). H=p²/2+x²/2

(3). H=1/2 (p-x)²+x²/2

(4). H=1/2 (p+x)²-x²/2

(5). правильна відповідь відсутня

774.

Для лаґранжіана L = ^x

— xx — x знайдіть гамільтоніан та виберіть варіант правильної

2

2

відповіді

(1). H=p²/2-x/2

(2). H=1/2 (p+x)2+x

(3). H=1/2 (p-x)²+x²/2

(4). H=1/2 (p+x)²-x²/2

(5). правильна відповідь відсутня

775.

(1).

(2).

(3).

(4).

Для гамільтоніану H=pq, одне з канонічних рівнянь має вигляд

(5). правильна відповідь відсутня

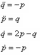776.

(1).

(2).

(3).

(4).

Для гамільтоніану H=p²-pq, одне з канонічних рівнянь має вигляд

(5). правильна відповідь відсутня

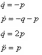777.

(1).

(2).

(3).

(4).

Для гамільтоніану H=1/2 (p+q)² одне з канонічних рівнянь має вигляд

(5). правильна відповідь відсутня

778.

(1).

(2).

(3).

(4).

Для гамільтоніану H=1/2 (p+q)²+q² одне з канонічних рівнянь має вигляд

(5). правильна відповідь відсутня

779.

h

Виберіть властивості дужок Пуассона, які виконуються для довільних функцій f, g та

(1). {f,g} = -{g,f}

(2). {f, const} = f

(3). {f ²,g} = 2f{f,g}

(4). {f,g-h}={f,g}-{f,h}

(5). {f,{g,h}}+{g,{h,f}}+{h,{f,g}}=0

780.

(1). 0

(2). 1

(3). p

(4). q

Дужка Пуассона {q,p} рівна

(5). правильна відповідь відсутня

781.

(1). 0

(2). 1

(3). qp

(4). q

Дужка Пуассона {q²,p} рівна

(5). правильна відповідь відсутня

782.

(1). 0

(2). 2qp

(3). qp

Дужка Пуассона {q²,p²} рівна

(4). q²-p²

(5). правильна відповідь відсутня

783.

(1). 0

Дужка Пуассона {cos p,p²} рівна

(2). 2qsin p

(3). 2psin p

(4). p²sin p

(5). правильна відповідь відсутня

784.

(1). 0

Дужка Пуассона {cos p,q} рівна

(2). sin p

(3). -cos p

(4). cos q

(5). правильна відповідь відсутня

785.

(1). 0

Дужка Пуассона {cos p,q sin p} рівна

(2). sin p

(3). cos p

(4). sin²p

(5). правильна відповідь відсутня

786.

Дужка Пуассона { p,q sin p} рівна

(1). -sinp

(2). p sin p

(3). 2p cos p

(4). 2sin p

(5). правильна відповідь відсутня

787.

Дужка Пуассона { p²,q sin p} рівна

(1). sinp

(2). 2sin p

(3). 2cos p

(4). -2p sinp

(5). правильна відповідь відсутня

788.

Дужка Пуассона { p²,q sh p} рівна

(1). sh p

(2). 2sh p

(3). 2ch p

(4). -2p sh p

(5). правильна відповідь відсутня

789.

Гамільтоніан вільної частинки рівний

(1). p/m

(2). p/2m + kx²/2 (3). p²/2m + U(x)

(4). p²/2m

(5). правильна відповідь відсутня

790.

Гамільтоніан є функцією від

(1). координат, імпульсів та часу (2). координат, швидкостей та часу (3). імпульсів, швидкостей та часу

(4). координат, імпульсів, швидкостей та часу

(5). правильна відповідь відсутня

791.

Гамільтоніан гармонічного осцилятора рівний

(1). p/m

(2). p²//2m + kx²/2 (3). p²/2m + U(x)

(4). p²/2m

(5). правильна відповідь відсутня

792.

Канонічними перетвореннями називають такі перетворення, при яких

(1). зберігається вигляд рівнянь Гамільтона (2). зберігається вигляд рівнянь Лаґранжа

(3). зберігаються фундаментальні дужки Пуасона та вигляд рівнянь Гамільтона (4). зберігається імпульс

(5). правильна відповідь відсутня

793.

Виберіть одну з умов, яку повинна задовільняти твірна функція канонічного

перетворення F₁=F₁(q_i,Q_i,t)

(1). p_i=∂F₁/∂q_i

(2). p_i=-∂F₁/∂q_i

(3). p_i=∂F₁/∂Q_i

(4). p_i=-∂F₁/∂q_i

(5). правильна відповідь відсутня

794.

Виберіть одну з умов, яку повинна задовільняти твірна функція канонічного

перетворення F₂=F₂(q_i,P_i,t)

(1). Q_i=-∂F₂/∂P_i

(2). Q_i=∂F₂/∂P_i

(3). Q_i=∂F₂/∂p_i

(4). Q_i=-∂F₂/∂p_i

(5). правильна відповідь відсутня

795.

Виберіть одну з умов, яку повинна задовільняти твірна функція канонічного

перетворення F₃=F₃(p_i,Q_i,t)

(1). q_i=∂F₃/∂p_i

(2). q_i=-∂F₃/∂p_i

(3). q_i=∂F₃/∂Q_i

(4). q_i=-∂F₃/∂Q_i

(5). правильна відповідь відсутня

796.

Виберіть одну з умов, яку повинна задовільняти твірна функція канонічного

перетворення F₄=F₄(p_i,P_i,t)

(1). q_i=∂F₄/∂P_i

(2). q_i=-∂F₄/∂P_i

(3). q_i=∂F₄/∂p_i

(4). q_i=-∂F₄/∂p_i

(5). правильна відповідь відсутня

797.

Диференціали твірних функцій dF₁(q_i,Q_i,t) та dF₂(q_i,P_i,t) пов'язані співвідношенням:

(1). dF₂=dF₁-d(Q_iP_i)

(2). dF₂=dF₁+d(Q_iP_i)

(3). dF₂=dF₁-d(q_ip_i)

(4). dF₂=dF₁+d(q_ip_i)

(5). правильна відповідь відсутня

798.

Використовуючи рівняння Гамільтона-Якобі знайти закон руху частинки масою m=1 у

потенціальному полі U=4-2x та вказати правильний варіант відповіді

(1). x(t)=-E/2 -1/2 -2(β+t)²

(2). x(t)=-E/2 -4 -4(β+t)^1/2

(3). x(t)=-E/2 -1-2(β+t)²

(4). x(t)=-E/2 +2+(β+t)²

(5). x(t)=-E/2 -1/2 +(β+t)²

799.

Використовуючи рівняння Гамільтона-Якобі знайти закон руху частинки масою m у

потенціальному полі U=5+x та вказати правильний варіант відповіді

(1). x(t)=E-(β+t)²/2m

(2). x(t)=E-(β+5t)²/2m

(3). x(t)=E-5-(β+t)²/2m

(4). x(t)=E-5-(β+5t)²/2m

(5). правильна відповідь відсутня

800.

Використовуючи рівняння Гамільтона-Якобі знайти закон руху частинки масою m у

потенціальному полі U=2+2x та вказати правильний варіант відповіді

(1). x(t)=E/2 -1-(β+t)²/m

(2). x(t)=E-(β+2t)²/2m

(3). x(t)=E-2-2(β+t)²/m

(4). x(t)=E-(β+t)²/2m

(5). x(t)=E-5-(β+5t)²/2m

801.

Використовуючи рівняння Гамільтона-Якобі знайти закон руху частинки масою m=1 у

потенціальному полі U=1-2x та вказати правильний варіант відповіді

(1). x(t)=E/2 -1/2 -(β+t)²

(2). x(t)=E/2 +1/2 -(β+t)^1/2

(3). x(t)=E/2 +1-2(β+t)²

(4). x(t)=E/2 -1/2 -2(β+t)²

(5). x(t)=E/2 +1/2 +(β+t)²

802.

Використовуючи рівняння Гамільтона-Якобі знайти закон руху частинки масою m=1 у

потенціальному полі U=3x+2 та вказати правильний варіант відповіді

(1). x(t)=E/3 -1/3 -1/3(β+t)² (2). x(t)=E/3 +2/3 +2/3(β+t)^1/2 (3). x(t)=E/3 -3-3(β+t)²

(4). x(t)=E/3 -2/3 -3/2(β+t)²

(5). x(t)=E/3 -1/3 +(β+t)²

803.

Знайдіть частоту малих коливань частинки масою m=1 в потенціальному полі

U=sin²(x) в околі положення рівноваги та виберіть варіант правильної відповіді

(1). ω=2

(2). ω=1

(3). ω=1/2

(4). ω=√2

(5). правильна відповідь відсутня

804.

Знайдіть частоту малих коливань частинки масою m=1 в потенціальному

полі U=cos²(x) в околі положення рівноваги та виберіть варіант правильної відповіді

(1). ω=2

(2). ω=1

(3). ω=√2

(4). ω=√1/2

(5). правильна відповідь відсутня

805.

Знайдіть частоту малих коливань частинки масою m=1 в потенціальному полі

U=tg²(ax), a >0 в околі положення рівноваги та виберіть варіант правильної відповіді

(1). ω=2a

(2). ω=a√2

(3). ω=a/2 √2

(4). ω=a/√2

(5). правильна відповідь відсутня

806.

Знайдіть частоту малих коливань частинки масою m=1 в потенціальному полі U=cos

(x) в околі положення рівноваги та виберіть варіант правильної відповіді

(1). ω=2

(2). ω=1

(3). ω=√2

(4). ω=1/2

(5). правильна відповідь відсутня

807.

Знайдіть частоту малих коливань частинки масою m=1 в потенціальному полі U=sin

(x) в околі положення рівноваги та виберіть варіант правильної відповіді

(1). ω=1

(2). ω=1/2

(3). ω=√2

(4). ω=1/4

(5). правильна відповідь відсутня

808.

Знайдіть частоту малих коливань частинки масою m=1 в потенціальному

полі U=tg (x) в околі положення рівноваги та виберіть варіант правильної відповіді

(1). ω=1

(2). ω=1/2

(3). правильна відповіль відсутня (4). ω=1/4

(5). ω=4

809.

Знайдіть частоту малих коливань частинки масою m=1 в потенціальному полі U=th (x)

в околі положення рівноваги та виберіть варіант правильної відповіді

(1). ω=1

(2). ω=1/2

(3). ω=√2

(4). правильна відповідь відсутня (5). ω=1/4

810.

Знайдіть частоту малих коливань частинки масою m=1 в потенціальному полі U=cth

(x) в околі положення рівноваги та виберіть варіант правильної відповіді

(1). ω=1

(2). ω=1/2

(3). ω=√2

(4). ω=1/4

(5). правильна відповідь відсутня

811.

Знайдіть частоту малих коливань частинки масою m=1 в потенціальному полі U=x² в

околі положення рівноваги та виберіть варіант правильної відповіді

(1). ω=1

(2). ω=1/2

(3). ω=√2

(4). ω=1/4

(5). правильна відповідь відсутня

812.

Знайдіть головні моменти інерції однорідної дротини масою m, яка має форму

стрижня довжиною 2a та виберіть варіант правильної відповіді

(1). I₁=0, I₂=I₃=ma²/3

(2). I₁=0, I₂=I₃=ma²/2

(3). I₁=I₂=0, I₃=ma²/3

(4). I₁=0, I₂=I₃=ma²

(5). правильна відповідь відсутня

813.

Знайдіть головні моменти інерції однорідної дротини масою m, яка має форму

квадрата зі стороною 2aта виберіть варіант правильної відповіді

(1). I₁=I₂=ma²/3, I₃=4ma²/3

(2). I₁=I₂=2ma²/3, I₃=4ma²/3

(3). I₁=I₂=2ma²/3, I₃=ma²/3

(4). I₁=0, I₂=I₃=ma²

(5). правильна відповідь відсутня

814.

Знайдіть головні моменти інерції однорідної дротини масою m, яка має форму кола

радіуса a та виберіть варіант правильної відповіді

(1). I₁=I₂=ma²/3, I₃=4ma²/3

(2). I₁=I₂=2ma²/3, I₃=4ma²

(3). I₁=I₂=ma²/2, I₃=ma²

(4). I₁=0, I₂=I₃=ma²

(5). правильна відповідь відсутня

815.

Знайдіть головні моменти інерції однорідної тонкої пластини масою m, яка має форму

квадрата зі стороною 2a та виберіть варіант правильної відповіді

(1). I₁=I₂=ma²/3, I₃=2ma²/3

(2). I₁=I₂=2ma²/3, I₃=4ma²

(3). I₁=I₂=2ma²/2, I₃=ma²

(4). I₁=0, I₂=I₃=ma²

(5). правильна відповідь відсутня

816.

Знайдіть головні моменти інерції однорідної тонкої пластини масою m, яка має форму

прямокутника зі сторонами 2a і 2b та виберіть варіант правильної відповіді

(1). I₁=ma²/3, I₂=mb²/3, I₃=2m(a²+b²)/3 (2). I₁=ma²/2, I₂=mb²/2, I₃=m(a²+b²)/2 (3). I₁=ma²/4, I₂=mb²/4, I₃=m(a²+b²)/4 (4). I₁=ma²/3, I₂=mb²/3, I₃=m(a²+b²)/3

(5). правильна відповідь відсутня

817.

Знайдіть головні моменти інерції однорідної тонкої пластини масою m, яка має форму

круга радіуса a та виберіть варіант правильної відповіді

(1). I₁=ma²/2, I₂=ma²/3, I₃=2ma²/3 (2). I₁=I₂=ma², I₃=2ma²

(3). I₁=I₂=ma²/4, I₃=ma²/2

(4). I₁=I₂=ma², I₃=ma²/2

(5). правильна відповідь відсутня

818.

Знайдіть головні моменти інерції однорідної тонкої сфери радіуса a масою m та

виберіть варіант правильної відповіді

(1). I₁=I₂=ma²/2, I₃=ma²

(2). I₁=I₂=I₃=ma²

(3). I₁=I₂=I₃=ma²/2

(4). I₁=I₂=I₃=2ma²/3

(5). правильна відповідь відсутня

819.

Знайдіть головні моменти інерції однорідної кулі радіуса a масою m та виберіть

варіант правильної відповіді

(1). I₁=I₂=I₃=ma²

(2). I₁=I₂=I₃=2ma²/3

(3). I₁=I₂=I₃=2ma²/5

(4). I₁=I₂=I₃=ma²/2

(5). правильна відповідь відсутня

820.

Знайдіть головні моменти інерції однорідного тіла масою m, яке має форму

прямокутного паралелепіпеда зі сторонами 2a, 2b і 2c та виберіть варіант правильної відповіді

(1). I₁=ma²/3, I₂=mb²/3, I₃=2mс²/3 (2). I₁=ma²/2, I₂=mb²/2, I₃=mс²/2

(3). I₁=ma(b²+c²)/2, I₂=m(a²+с²)/2, I₃=m(a²+b²)/2 (4). I₁=ma(b²+c²)/3, I₂=m(a²+с²)/3, I₃=m(a²+b²)/3

(5). правильна відповідь відсутня

821.

(1). 0

(2). 1

(3). 2

(4). 3