2.4 Расчет опн регулятора.
Путем изменения параметров настройки регулятора получим режим автоколебаний на электронной модели замкнутой САР в среде «VisSim». Зафиксируем критическое значение коэффициента пропорциональности регулятора и период колебаний. Рассчитаем оптимальные параметры настройки регулятора.
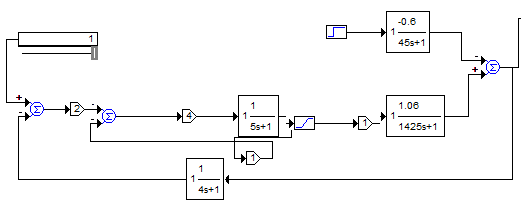
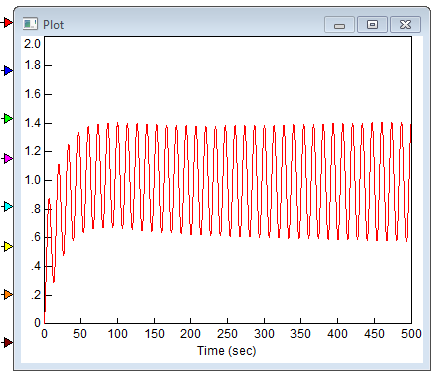
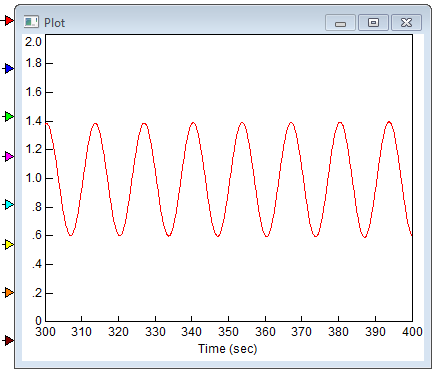
Рис. 9. Незатухающие колебания при критическом коэффициенте усиления
Предельный коэффициент усиления - 4; период незатухающих колебаний - 15 секунд.
Теперь рассчитаем оптимальные коэффициенты:
П Крег=0.5 К
Таблица 2 Оптимальные коэффициенты усиления для регулятора
Параметры при незатухающих колебаниях |
|
||||
К - коэффициент усиления регулятора |
То - период колебаний, сек |
Оптимальные параметры настройки регулятора |
|||
|
|
Закон регулирования |
Крег |
Ти |
Тд |
4 |
15 |
П |
2 |
∞ |
0 |
3. Статический анализ сар.
3.1. Статическая точность регулирования
Моделируем переходные процессы в замкнутой САР для трех видов расходных характеристик при изменения нагрузки λ от 0 до 1, фиксируем установившееся значения регулируемой величины φ∞. Строим статические характеристики САР φ∞ =f(λ).
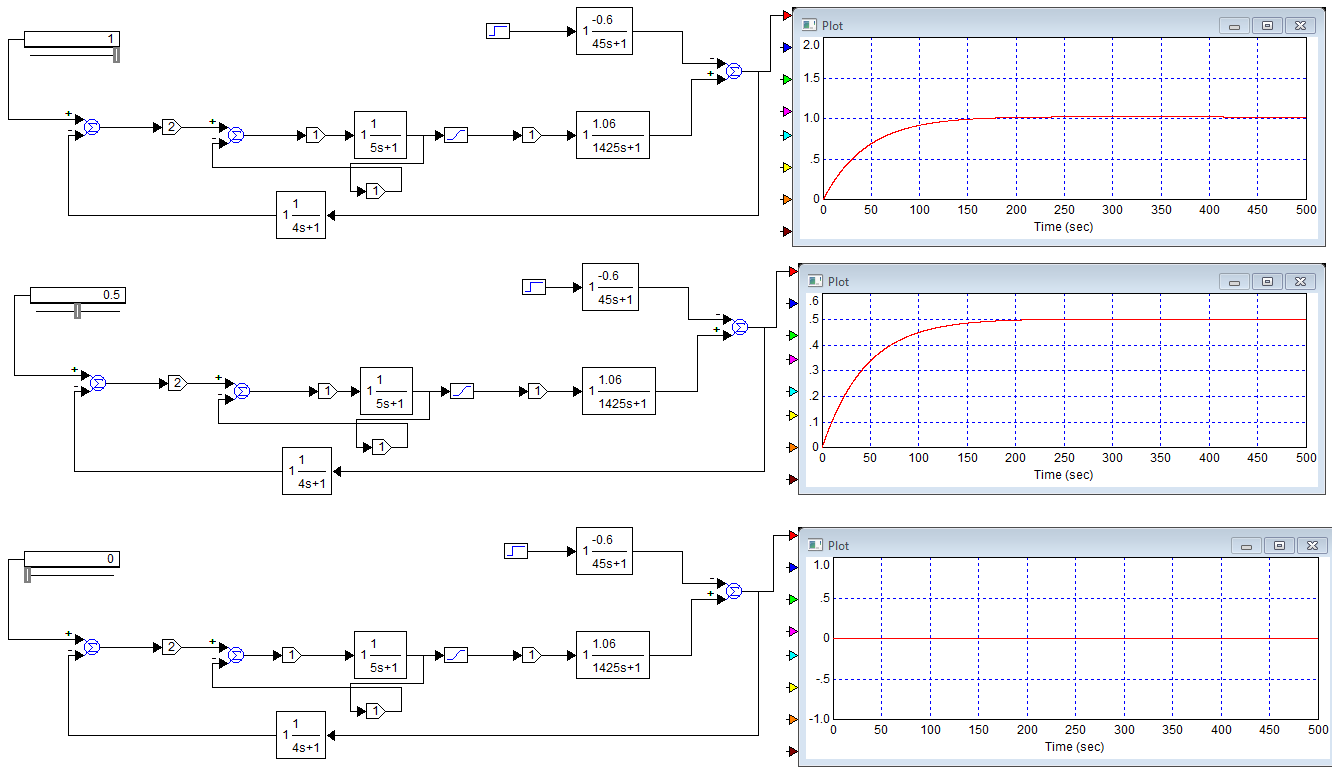
Рис. 10. Модель САР при 0; 50; 100 % нагрузки
Вывод: при увеличении нагрузки, растет время переходного процесса, что приводит к увеличению статической ошибки.
3.2 Анализ влияния зазоров в регулирующих органах на статические свойства сар
В связи с наличием трения, зазоров, перекрывшей в звеньях (например, в измерителе, усилителе и т.д.) САР реагирует не на все изменения регулируемой величины. Наибольшее отклонение регулируемой величины, на которое система не реагирует, называется нечувствительностью ΔYнеч
Проведем опыт, введем зону нечувствительности перед усилителем, в модель САР, затем будем менять значения зоны нечувствительности от 0 до 2, т.е. симулируем зазоры и люфты в У (усилителе), после этого строим зависимость выходного значения модели САР от нечувствительности усилителя.
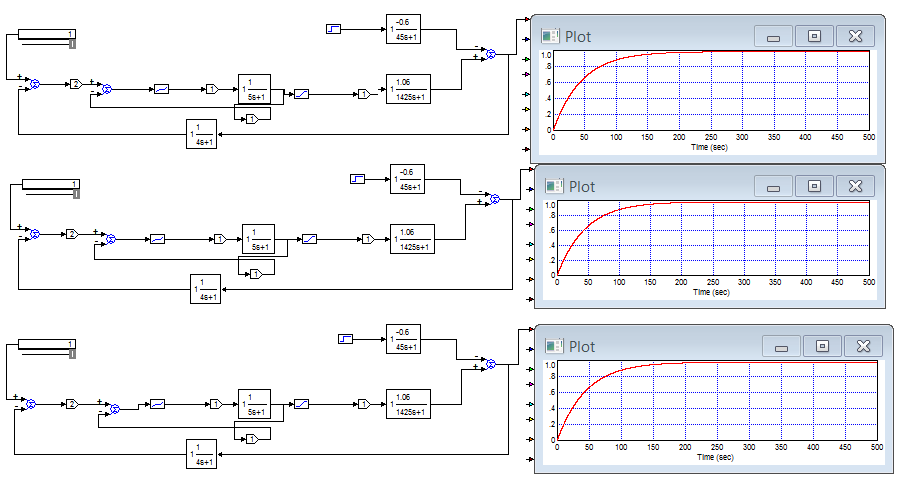
Рис. 11 Модель САР при ΔYнеч = 0; 0,1; 0,2
Вывод: Рост нечувствительности (зазоры, люфты), в моем случае усилителя, приводят к статической ошибки процесса регулирования.
4. Влияние отдельных элементов регулятора на качество САР.
4.1. Оценка влияния численных значений времени исполнительного механизма и инерционности датчика на показатели качества переходных процессов в заданной САР.
Фиксируем показатели качества переходных процессов при моделировании различных значений времени сервомотора и инерционности датчика.
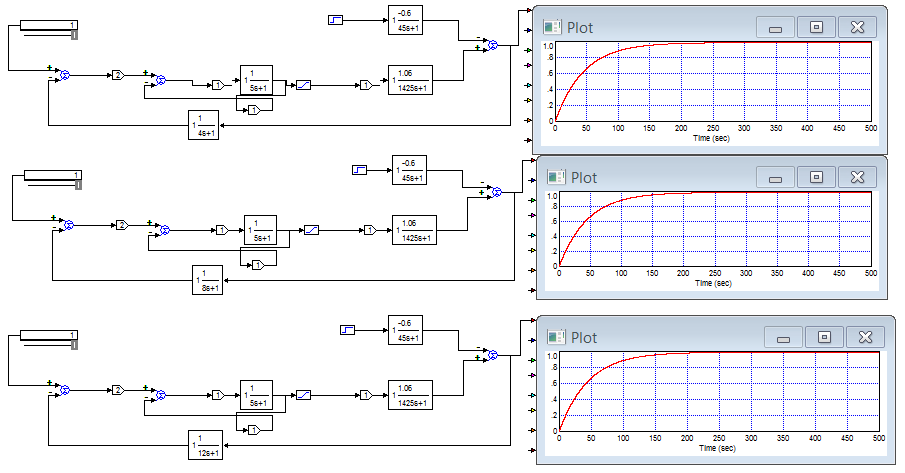
Рис. 12. Модель САР при Тд = 4; 8; 12.
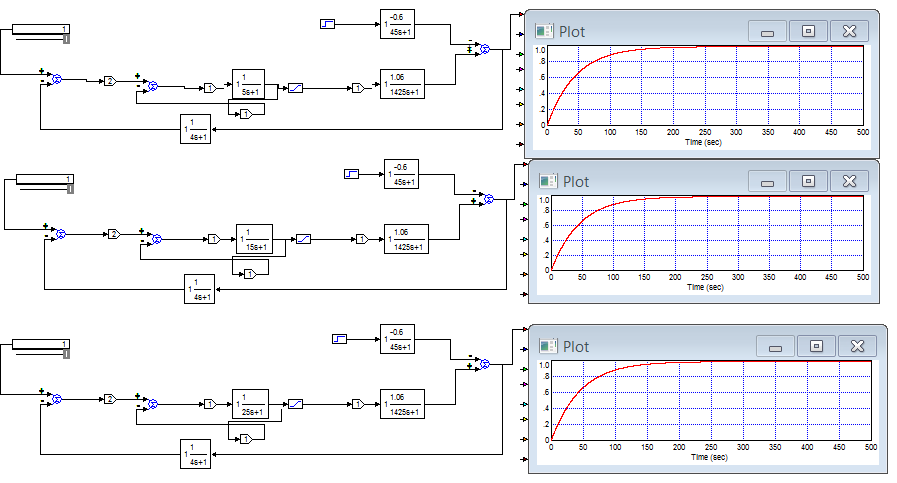
Рис. 13. Модель САР при Тим = 5; 15; 25.
4.2. Оценка влияния времени запаздывания датчика на устойчивость САР.
По мере роста запаздывания максимальное отклонение растет и показатель качества устойчивости ухудшается.
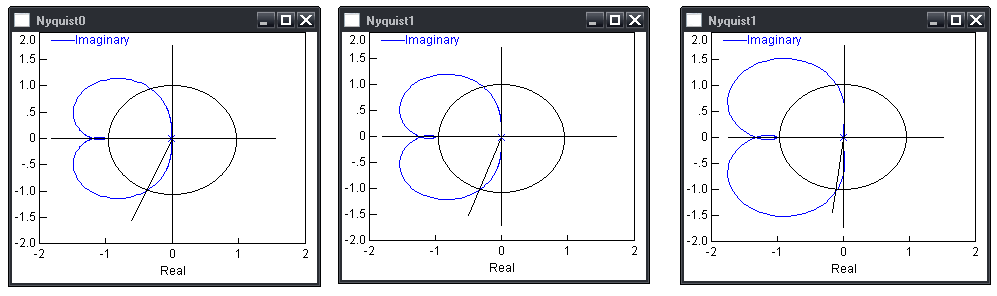
Рис. 14 АФЧХ при τ = 1; 2; 3 с.
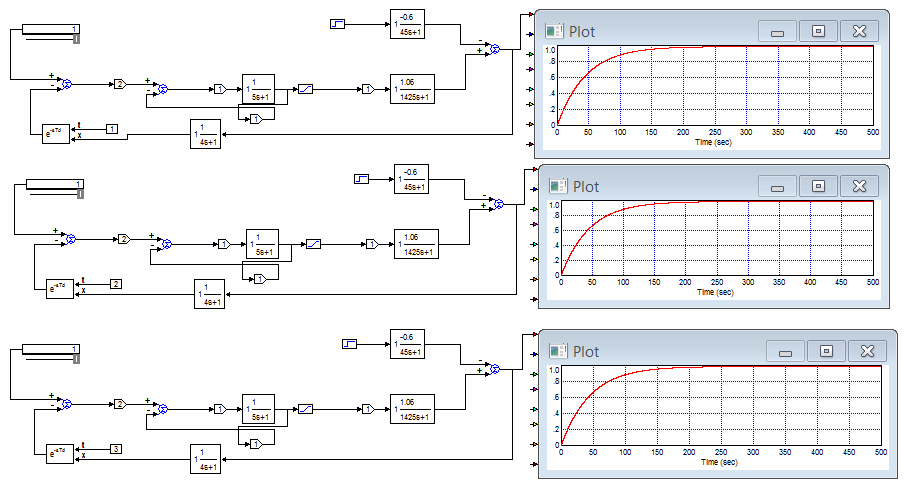
Рис. 15 Модель САР при τ = 1; 2; 3 с.
4.3. Оценка влияния нечувствительности регулятора на свойства САР.
Вводим в структурную схему САР звено (к выходу Д и ИМ), моделирующее нечувствительность регулятора с шириной зоны от 0 до 0,2; получим переходные функции замкнутой САР.
Рост коэффициента нечувствительности приводит к росту статической ошибки процесса регулирования. Допускается, статическая ошибка процесса регулирования от 0 до 10 %.
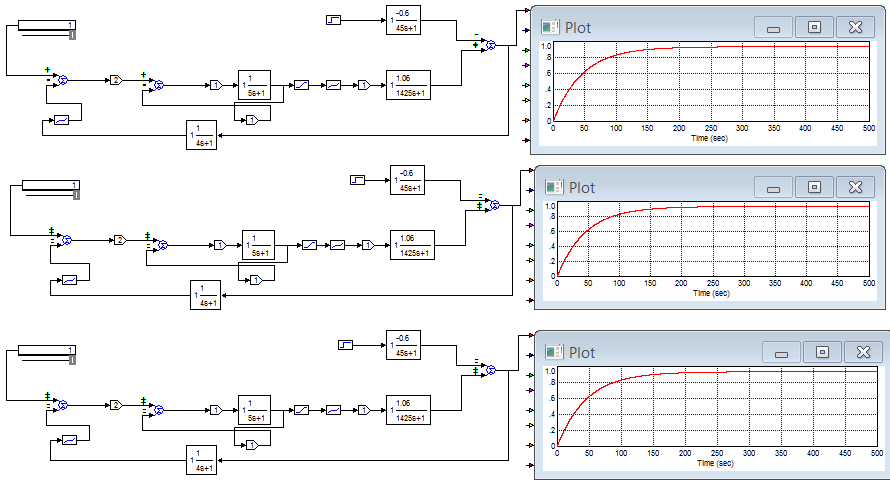
Рис. 16. Модель САР при коэффициентах нечувствительности 0; 0,1; 0,2.