
- •1 Вопрос
- •2 Вопрос Гармонические колебания. Пружинный маятник
- •3.Гармонические колебания. Математический маятник.
- •4. Гармонические колебания. Физический маятник
- •5) Свободные гармонические колебания в колебательном контуре
- •6) Сложение гармонических колебаний одного направления и одинаковой частоты, биения
- •Вопрос7. Сложение взаимно перпендикулярных колебаний. Фигуры Лиссажу.
- •Вопрос 8. Затухающие колебания
- •Вопрос 9 . Вынужденные колебания. Резананс
- •Вопрос 10. Переменный ток. Получение и основные характеристики
- •Вопрос 13 Сопротивление, емкость, индуктивность в цепи переменного тока.
- •Вопрос 14 Мощность, выделяемая в цепи переменного тока.
- •17. Электромагнитные волны и их характеристики.
- •18. Энергия и импульс электромагнитной волны.
- •21)Интерференция света. Опыт Юнга
- •22)Интерференция света в плоскопараллельной пластинке и тонком клинке
- •23) Кольца Ньютона
- •25.Дифракция света.Метод зон френеля.Диск
- •26.Дифракция Фраунгофера на прямоугольной щели
- •Вопрос 29. Поляризация. Закон Блюстера
- •Закон Брюстера
- •Вопрос 30. Оптическая анизотропия
- •(Вопр№31) Электронная теория дисперсии света. Аномальная и нормальная дисперсия света. Связь дисперсии и поглощения
- •(Вопр№32) Зависимость показателя преломления от частоты падающего света.
- •33. Поглощение света.Закон Бугера.
Вопрос 8. Затухающие колебания
ЗАТУХАЮЩИЕ КОЛЕБАНИЯ - колебания с постоянно убывающей со временем амплитудой.
Свободные колебания реальных систем всегда затухают. Затухание обусловлено в основном трением (механические системы) и сопротивлением ( в электромагнитных колебательных контурах).
Колебательная система называется линейной, если её свойства не меняются при колебаниях, то есть такие параметры, как сила тяжести, упругость пружины, сопротивление, емкость, индуктивность не зависят ни от смещения, ни от скорости, ни от ускорения колеблющейся величины. В дальнейшем мы будем рассматривать только линейные системы.
Уравнения затухающих колебаний
Получим дифференциальное уравнение свободных затухающих колебаний на примере реального пружинного маятника, совершающего колебания в среде с сопротивлением (простейший случай - трение о воздух). Пусть масса маятника m, коэффициент упругости пружины k, сила сопротивления, действующая на маятник, F = - bv, v - скорость маятника, b - коэффициент сопротивления среды, в которой находится маятник. Так как мы рассматриваем только линейные системы, b = const, k = const. x - смещение маятника от положения равновесия.
Второй закон Ньютона в нашем случае запишется так:
Это уравнение и есть дифференциальное уравнение свободных затухающих колебаний пружинного маятника. Его, однако, принято записывать в следующем, так называемом каноническом виде:
- коэффициент затухания, - собственная частота свободных (незатухающих) колебаний пружинного маятника, то, что раньше мы обозначали просто w.
Уравнение затухающих колебаний в таком (каноническом) виде описывает затухающие колебания всех линейных систем; конкретная колебательная система отличается только выражениями для b и j0.
Вопрос 9 . Вынужденные колебания. Резананс
Вынужденные колебания — колебания, происходящие под воздействием внешних периодических сил.
Автоколебания отличаются от вынужденных колебаний тем, что последние вызваны периодическим внешним воздействием и происходят с частотой этого воздействия, в то время как возникновение автоколебаний и их частота определяются внутренними свойствами самой автоколебательной системы.
Наиболее
простой и содержательный пример
вынужденных колебаний можно получить
из рассмотрения гармонического
осциллятора и вынуждающей силы, которая
изменяется по закону: .
![]()
Вынужденные колебания гармонического осциллятора[править]
Консервативный гармонический осциллятор[править]
Второй
закон Ньютона для такого осциллятора
запишется в виде:
![]() . Если ввести обозначения:
. Если ввести обозначения:
![]() и заменить ускорение на вторую производную
от координаты по времени, то получим
следующее обыкновенное дифференциальное
уравнение:
и заменить ускорение на вторую производную
от координаты по времени, то получим
следующее обыкновенное дифференциальное
уравнение:
![]()
Решением этого уравнения будет сумма общего решения однородного уравнения и частного решения неоднородного. Общее решение однородного уравнения было уже получено здесь и оно имеет вид:
,
![]()
где
![]() —
произвольные постоянные, которые
определяются из начальных условий.
—
произвольные постоянные, которые
определяются из начальных условий.
Найдём
частное решение. Для этого подставим в
уравнение решение вида:
![]() и получим значение для константы:
и получим значение для константы:
![]()
Тогда
окончательное решение запишется в виде:
![]()
Эффект резонанса для разных частот внешнего воздействия и коэффициентов затухания
Резонанс[править]
Из
решения видно, что при частоте вынуждающей
силы, равной частоте свободных колебаний,
оно не пригодно — возникает резонанс,
то есть «неограниченный» линейный рост
амплитуды со временем. Из курса
математического анализа известно, что
решение в этом случае надо искать в
виде:
![]() .
Подставим этот анзац в дифференциальное
уравнение и получим, что :
.
Подставим этот анзац в дифференциальное
уравнение и получим, что :
![]()
Таким образом, колебания в резонансе будут описываться следующим соотношением:
![]()
Затухающий гармонический осциллятор[править
Второй закон Ньютона:
.
![]()
Переобозначения:
![]()
Дифференциальное
уравнение:
![]()
Его решение будет строиться, как сумма решений однородного уравнения и частного решения неоднородного. Анализ однородного уравнения приведён здесь. Получим и проанализируем частное решение.
Запишем
вынуждающую силу следующим образом:![]() ,
тогда решение будем искать в виде:
,
тогда решение будем искать в виде:
![]() .
Подставим это решение в уравнение и
найдём выражение для A:
.
Подставим это решение в уравнение и
найдём выражение для A:

где

Полное решение имеет вид:
,
где![]() — собственная частота затухающих
колебаний.
— собственная частота затухающих
колебаний.
Константы
C1иC2
в каждом из случаев определяются из
начальных условий:
![]()
В этом случае, в отличие от осциллятора без трения, амплитуда колебаний в резонансе имеет конечную величину.
Если
мы рассмотрим устоявший процесс, то
есть ситуацию при![]() , то решение однородного уравнения будет
стремиться к нулю и останется только
частное решение:
, то решение однородного уравнения будет
стремиться к нулю и останется только
частное решение: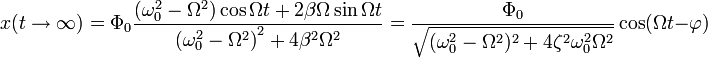
Это означает, что при система «забывает» начальные условия, и характер колебаний зависит только от вынуждающей силы.
Работа,
совершаемая вынуждающей силой
![]() за время
за время![]() ,
равна
,
равна![]() , а мощность
, а мощность![]() . Из уравнения
. Из уравнения
следует,
что![]()
Если учесть, что при установившихся вынужденных колебаниях
![]()
![]()
![]()
то
nогда
средняя за период![]() мощность:
мощность:
![]()
Работа
за период![]()
