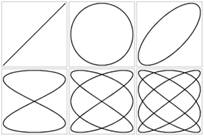
Вопрос7. Сложение взаимно перпендикулярных колебаний. Фигуры Лиссажу.

Фигуры Лиссажу́ — замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два гармонических колебания в двух взаимно перпендикулярных направлениях. Впервые изучены французским учёным Ж. Лиссажу (J. Lissajous; 1822—80). Вид фигур зависит от соотношения между периодами (частотами), фазами и амплитудами обоих колебаний. В простейшем случае равенства обоих периодов фигуры представляют собой эллипсы, которые при разности фаз 0 или π вырождаются в отрезки прямых, а при разности фаз π/2 и равенстве амплитуд превращаются в окружность. Если периоды обоих колебаний неточно совпадают, то разность фаз всё время меняется, вследствие чего эллипс всё время деформируется. При существенно различных периодах фигуры Лиссажу не наблюдаются. Однако, если периоды относятся как целые числа, то через промежуток времени, равный наименьшему кратному обоих периодов, движущаяся точка снова возвращается в то же положение — получаются фигуры Лиссажу более сложной формы. Фигуры Лиссажу вписываются в прямоугольник, центр которого совпадает с началом координат, а стороны параллельны осям координат и расположены по обе стороны от них на расстояниях, равных амплитудам колебаний.

Свободные затухающие колебания. Характеристики затухания: коэффициент затухания, время релаксации, декремент затухания, добротность колебательной системы.

Затуханием колебаний называется постепенное ослабление колебаний с течением времени, обусловленное потерей энергии колебательной системой. Закон затухания колебаний зависит от свойств колебательной системы. Система называется линейной, если параметры, характеризующие существенные в рассматриваемом процессе физические свойства системы, не изменяются в ходе процесса. Свободные затухающие колебания линейной системы описываются уравнением:

где - коэффициент затухания, - собственная частота системы, т.е. частота, с которой совершались бы колебания в отсутствии затухания. Выражение коэффициента затухания через параметры системы зависит от вида колебательной системы. Два тела, массы которых одинаковы, движутся навстречу друг другу, при этом скорость одного тела в 2 раза больше скорости второго. Какая часть механической энергии системы перейдет во внутреннюю энергию при центральном абсолютно неупругом ударе?

Для решения уравнения

производится подстановка .Эта подстановка приводит к характеристическому уравнению:

которое имеет два корня:

При не слишком большом затухании (при ) подкоренное выражение будет отрицательным. Если его представить в виде где - вещественная положительная величина, называемая циклической частотой затухающих колебаний и равная

то корни уравнения запишутся в виде:

Общим решением уравнения будет функция:

которую можно представить в виде:

Здесь и - произвольные постоянные.

движение системы можно условно рассматривать как гармоническое колебание частоты w с амплитудой, изменяющейся по закону:

Период затухающих колебаний определяется формулой:

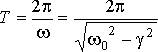
При незначительном затухании период колебаний практически равен

Такое отношение амплитуд называется декрементом затухания, а его натуральный логарифм - логарифмическим декрементом затухания:

Логарифмический декремент затухания обратен по величине числу колебаний, совершаемых за то время, за которое амплитуда уменьшается в «e» раз.

Помимо рассмотренных величин для характеристики колебательной системы употребляется величина

называемая добротностью колебательной системы. Добротность пропорциональна числу колебаний, совершаемых системой за то время, за которое амплитуда колебаний уменьшается в «e» раз.

время релаксации — время, за которое амплитуда колебаний уменьшится в e раз.

Вращательное движение - это движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения. Система отсчета - совокупность системы координат и часов, связанных с телом отсчета. Траектория движения материальной точки - линия, описываемая этой точкой в пространстве. Длина участка траектории, пройденного материальной точкой с момента начала отсчета времени, называется длиной пути.