
- •1 Вопрос
- •2 Вопрос Гармонические колебания. Пружинный маятник
- •3.Гармонические колебания. Математический маятник.
- •4. Гармонические колебания. Физический маятник
- •5) Свободные гармонические колебания в колебательном контуре
- •6) Сложение гармонических колебаний одного направления и одинаковой частоты, биения
- •Вопрос7. Сложение взаимно перпендикулярных колебаний. Фигуры Лиссажу.
- •Вопрос 8. Затухающие колебания
- •Вопрос 9 . Вынужденные колебания. Резананс
- •Вопрос 10. Переменный ток. Получение и основные характеристики
- •Вопрос 13 Сопротивление, емкость, индуктивность в цепи переменного тока.
- •Вопрос 14 Мощность, выделяемая в цепи переменного тока.
- •17. Электромагнитные волны и их характеристики.
- •18. Энергия и импульс электромагнитной волны.
- •21)Интерференция света. Опыт Юнга
- •22)Интерференция света в плоскопараллельной пластинке и тонком клинке
- •23) Кольца Ньютона
- •25.Дифракция света.Метод зон френеля.Диск
- •26.Дифракция Фраунгофера на прямоугольной щели
- •Вопрос 29. Поляризация. Закон Блюстера
- •Закон Брюстера
- •Вопрос 30. Оптическая анизотропия
- •(Вопр№31) Электронная теория дисперсии света. Аномальная и нормальная дисперсия света. Связь дисперсии и поглощения
- •(Вопр№32) Зависимость показателя преломления от частоты падающего света.
- •33. Поглощение света.Закон Бугера.
3.Гармонические колебания. Математический маятник.
Гармонические колебания — колебания, при которых физическая (или любая другая) величина изменяется с течением времени по синусоидальному или косинусоидальному закону. Кинематическое уравнение гармонических колебаний имеет вид
или
,
где х — смещение (отклонение) колеблющейся точки от положения равновесия в момент времени t; А — амплитуда колебаний, это величина, определяющая максимальное отклонение колеблющейся точки от положения равновесия; ω — циклическая частота, величина, показывающая число полных колебаний происходящих в течение 2π секунд; — полная фаза колебаний, — начальная фаза колебаний.
Обобщенное гармоническое колебание в дифференциальном виде
Математи́ческий ма́ятник — осциллятор, представляющий собой механическую систему, состоящую из материальной точки, находящейся на невесомой нерастяжимой нити или на невесомом стержне в однородном поле сил тяготения. Период малых собственных колебаний математического маятника длины L неподвижно подвешенного в однородном поле тяжести с ускорением свободного падения g равен
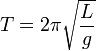
и не зависит от амплитуды колебаний и массы маятника.
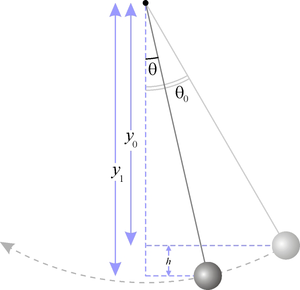
Маятник, совершающий малые колебания, движется по синусоиде. Поскольку уравнение движения является обыкновенным ДУ второго порядка, для определения закона движения маятника необходимо задать два начальных условия — координату и скорость, из которых определяются две независимых константы:
![]()
где
— амплитуда колебаний
маятника, ![]() —
начальная фаза колебаний,
— циклическая
частота, которая определяется из
уравнения движения. Движение, совершаемое
маятником, называется гармоническими
колебаниями.
—
начальная фаза колебаний,
— циклическая
частота, которая определяется из
уравнения движения. Движение, совершаемое
маятником, называется гармоническими
колебаниями.
4. Гармонические колебания. Физический маятник
Гармонические колебания — колебания, при которых физическая (или любая другая) величина изменяется с течением времени по синусоидальному или косинусоидальному закону. Кинематическое уравнение гармонических колебаний имеет вид
или
,
где х — смещение (отклонение) колеблющейся точки от положения равновесия в момент времени t; А — амплитуда колебаний, это величина, определяющая максимальное отклонение колеблющейся точки от положения равновесия; ω — циклическая частота, величина, показывающая число полных колебаний происходящих в течение 2π секунд; — полная фаза колебаний, — начальная фаза колебаний.
Обобщенное гармоническое колебание в дифференциальном виде
Физический маятник — Осциллятор, представляющий собой твёрдое тело, совершающее колебания в поле каких-либо сил относительно точки, не являющейся центром масс этого тела, или неподвижной оси, перпендикулярной направлению действия сил и не проходящей через центр масс этого тела.
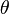 —
угол
отклонения маятника от равновесия;
—
угол
отклонения маятника от равновесия;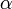 —
начальный
угол отклонения маятника;
—
начальный
угол отклонения маятника;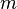 —
масса
маятника;
—
масса
маятника;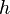 —
расстояние
от точки подвеса до центра тяжести
маятника;
—
расстояние
от точки подвеса до центра тяжести
маятника; —
радиус
инерции относительно оси, проходящей
через центр тяжести.
—
радиус
инерции относительно оси, проходящей
через центр тяжести.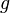 —
ускорение
свободного падения.
—
ускорение
свободного падения.
Момент инерции относительно оси, проходящей через точку подвеса:
![]() .
.
Пренебрегая сопротивлением среды, дифференциальное уравнение колебаний физического маятника в поле силы тяжести записывается следующим образом:
![]() .
.
Полагая ![]() ,
предыдущее уравнение можно переписать
в виде:
,
предыдущее уравнение можно переписать
в виде:
![]() .
.
Центр качания — точка, в которой надо сосредоточить всю массу физического маятника, чтобы его период колебаний не изменился.
Поместим
на луче,
проходящем от точки подвеса через центр
тяжести точку на расстоянии ![]() от
точки подвеса. Эта точка и будет центром
качания маятника.
от
точки подвеса. Эта точка и будет центром
качания маятника.
Действительно,
если всю массу сосредоточить в центре
качания, то центр качания будет совпадать
с центром масс. Тогда момент инерции
относительно оси подвеса будет равен ![]() ,
а момент
силы тяжести относительно
той же оси
,
а момент
силы тяжести относительно
той же оси ![]() .
Легко заметить, что уравнение движения
не изменится.
.
Легко заметить, что уравнение движения
не изменится.
Теорема Гюйгенса
Если физический маятник подвесить за центр качания, то его период колебаний не изменится, а прежняя точка подвеса сделается новым центром качания.
Если амплитуда колебаний мала, то корень в знаменателе эллиптического интеграла приближенно равен единице. Такой интеграл легко берется, и получается хорошо известная формула малых колебаний:
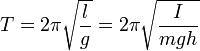 .
.
Эта формула даёт результаты приемлемой точности (ошибка менее 1 %) при углах, не превышающих 4°.
Следующий порядок приближения можно использовать с приемлемой точностью (ошибка менее 1 %) при углах до 1 радиана (≈60°)
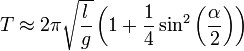 .
.
