26.Дифракция Фраунгофера на прямоугольной щели

ДИФРАКЦИЯ ФРАУНГОФЕРА НА ЩЕЛИ

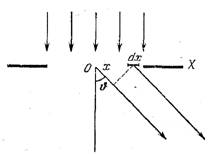
Простейшим для расчета и практически очень важным случаем является фраунгоферова дифракция на длинной прямоугольной щели (Дифракция Фраунгофера на щели). Ширину щели обозначим через b, ее длину будем считать бесконечной. Пусть на щель нормально падает плоская монохроматическая волна (рис. 5.7.1). Световое поле за щелью найдется по принципу Гюйгенса как результат интерференции когерентных вторичных волн, исходящих из различных точек волнового фронта на щели. Вторичные волны, излучаемые полоской волнового фронта ширины dx, параллельной щели, складываясь, дают цилиндрическую волну, осью которой является эта полоска. Зависимость этой волны от направления ее распространения, определяемого углом j должен предполагаться малым. Однако необходимо учесть разности фаз между волнами, исходящими из различных полосок. Разумеется, речь идет о фазах колебаний на бесконечном расстоянии от щели. Волна, исходящая из dx под углом j, опережает по фазе волну того же направления, исходящую из середины щели О, на kx sinj.

Поэтому результирующее поле в бесконечности, создаваемое всей щелью, представиться интегралом

Здесь опущены все множители, не являющиеся на относительное распределение волнового поля по направлениям. Вычислив интеграл, получим

Где введено обозначение

Отсюда для распределения интенсивности света по направлениям найдем 

Где  - интенсивность в направлении падающей волны. Обе функции обращаются в максимум, равной единице, при a=0. При  , где m=1,2 они равны 0. Между двумя соседними минимумами располагаются максимумы различных порядков. Их положения определяются трансцендентным уравнением a cos-sina=0. Практически можно считать, что максимумы располагаются посередине между соседними минимумами.

Вопрос №27 Дифракция Фраунгофера от прямоугольной щели.

Рассмотрим дифракцию Фраунгофера на узкой прямоугольной щели. Пусть пучок параллельных лучей монохроматического света падает перпендикулярно на узкую прямоугольную щель шириной   в непрозрачном экране Э1 (рис.6). За щелью расположена линза  , которая собирает лучи на экране Э2, помещенном в ее фокальной плоскости (рис.7). Если бы при прохождении света через щель соблюдался закон прямолинейного распространения света, то на экране Э2 получилось бы изображение прямоугольной щели.

    

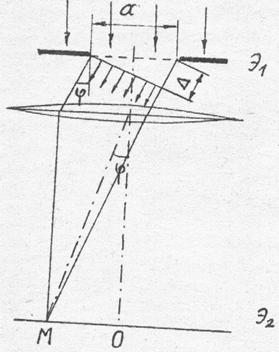
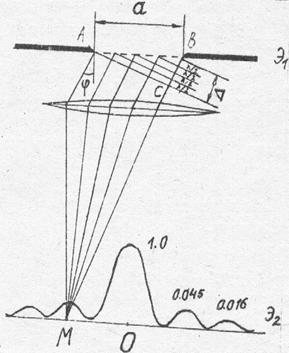
 Рис.6 Рис.7

Вследствие дифракции картина коренным образом изменяется: на экране наблюдается система интерференционных максимумов – размытых изображений щели, разделенных темными промежутками интерференционных минимумов.

Согласно принципу Гюйгенса, каждый элемент поверхности световой волны АВ является источником когерентных волн, распространяющихся в различных направлениях. Из всех возможных направлений выберем одно – под углом   относительно нормали к плоскости щели. Лучи, идущие из разных участков щели АВ под углом   по отношению к их первоначальному направлению, соберутся линзой в точке М. Они пройдут разные пути и будут сдвинуты по фазе. Результат их интерференции в точке М зависит от угла    и ширины щели.

Для объяснения полученной картины воспользуемся методом зон Френеля и выполним следующее построение. Через крайнюю точку А щели (см. рис.7) проведем плоскость АС, перпендикулярную направлению дифрагированных лучей. Тогда отрезок ВС будет представлять собой раз-ность хода крайних-лучей. Разделим его на ряд отрезков длиной  . Число таких отрезков   будет равно

  (4)

Через концы этих отрезков проведем плоскости, параллельные плоскости АС, до пересечения с открытой частью волновой поверхности АВ. Фронт волны АВ разобьется на   полосок одинаковой ширины, являющихся зонами Френеля. Колебания, приходящие в точку М от любой пары соседних зон, имеют разность хода   и, находясь в противоположных фазах, ослабляют друг друга. Следовательно, ослабление света (дифракционный минимум) в точке М наблюдается при четном числе   ( ), а усиление (дифракционный максимум) – при нечетном числе   ( ). Таким образом, из формулы (4) получим условия минимумов и максимумов освещенности:

  (5)

 (6)

где 

Дифракционная картина от одной щели представляет собой чередование светлых и темных полос около нейтрального максимума, которому соответствует условие  . Число и называется порядком, дифракционного максимума: числу   соответствует максимум нулевого порядка, числам   и   – максимумы первого и второго порядков соответственно. На рис.7 указаны положение и интенсивности дифракционных максимумов. Область, лежащую между   и  , занимает центральная светлая полоса. Чем меньше длина волны и больше ширина щели, тем уже эта полоса. Положение максимумов и минимумов на экране Э2 зависят от длины падающей световой волны, Если падающий свет сложный, например, состоит из двух монохроматических излучений с длинами волн    и  , то на экране максимумы и минимумы этих волн располагаются а разных местах. Большим   соответствуют большие углы отклонения.

В дальнейшем, с развитием теории электромагнетизма было установлено, что свет представляет собой электромагнитную волну, а с развитием представлений о пространстве и времени (теория относительности) отпала надобность в эфире, в котором распространяются электромагнитные колебания. Однако, несмотря на достижения волновой теории света в объяснении различных явлений, выявились и ее затруднения. 

Вопрос №28 Поляризация света.Закон Малюса.

Закон Малюса — физический закон, выражающий зависимость интенсивности линейно-поляризованного света после его прохождения через поляризатор от угла   между плоскостями поляризации падающего света и поляризатора.

где   — интенсивность падающего на поляризатор света,   — интенсивность света, выходящего из поляризатора,   — коэффициент пропускания поляризатора.

Установлен Э. Л. Малюсом в 1810 году.

В релятивистской форме

где   и   — циклические частоты линейно поляризованных волн, падающей на поляризатор и вышедшей из него.

Свет с иной (не линейной) поляризацией может быть представлен в виде суммы двух линейно-поляризованных составляющих, к каждой из которых применим закон Малюса. По закону Малюса рассчитываются интенсивности проходящего света во всех поляризационных приборах, например в поляризационных фотометрах и спектрофотометрах. Потери на отражение, зависящие от   и не учитываемые законом Малюса, определяются дополнительно.