22)Интерференция света в плоскопараллельной пластинке и тонком клинке

Получить две когерентные волны можно и другим методом - делением амплитуды первичной волны.

Если световая волна с плоским фронтом падает на плоскопараллельную пластину, то она отражается и преломляется на обеих сторонах пластины (рис. 3.3). Будем рассматривать волны 1 и 2. Эти волны имеют одинаковые частоты  . Разность фаз  , т.к. она определяется только условиями отражения и преломления. Следовательно, волны 1 и 2 когерентны. Их разность хода  , где   - толщина пластины,   - ее показатель преломления,   - угол падения. Волны 1 и 2 параллельны. Это означает, что они сходятся только на бесконечности и там образуют интерференционную картину, которую называют линиями равного наклона.

Рис. 3.3. Интерференция света в плоскопараллельной пластине 

В оптических экспериментах, где толщина пластин мала (у нас d≈0,1 мм), бесконечно далекое расстояние до экрана наблюдения соответствует нескольким метрам.

Для наблюдения изображения интерференционной картины можно воспользоваться линзой.

Делить падающую волну можно и клиновидной пластиной. Мы также получим две когерентные волны. Но они переналожатся вблизи поверхности клина. Они будут интерферировать вблизи поверхности клина. Чтобы наблюдать такую картину (ее называют линии равной толщины), надо использовать линзу (рис. 3.4).

Рис.3.4. Интерференция света в тонком клине 

Если угол клина мал, то разность хода  , т.е. точно также считается, как и в случае с плоскопараллельной пластиной.

23) Кольца Ньютона

Ко́льца Нью́тона — кольцеобразные интерференционные максимумы и минимумы, появляющиеся вокруг точки касания слегка изогнутой выпуклой линзы и плоскопараллельной пластины при прохождении света сквозь линзу и пластину^[1]. Интерференционная картина в виде концентрических колец (колец Ньютона) возникает между поверхностями одна из которых плоская, а другая имеет большой радиус кривизны (например, стеклянная пластинка и плосковыпуклая линза). Исаак Ньютон исследовав их в монохроматическом и белом свете обнаружил, что радиус колец возрастает с увеличением длины волны (от фиолетового к красному).

Удовлетворительно объяснить, почему возникают кольца, Ньютон не смог. Удалось это Юнгу. Проследим за ходом его рассуждений. В их основе лежит предположение о том, что свет — это волны. Рассмотрим случай, когда монохроматическая волна падает почти перпендикулярно на плосковыпуклую линзу.

Пример колец Ньютона

Волна 1 появляется в результате отражения от выпуклой поверхности линзы на границе стекло — воздух, а волна 2 — в результате отражения от пластины на границе воздух — стекло. Эти волны когерентны, то есть у них одинаковые длины волн, а разность их фаз постоянна. Разность фаз возникает из-за того, что волна 2 проходит больший путь, чем волна 1. Если вторая волна отстает от первой на целое число длин волн, то, складываясь, волны усиливают друг друга.

 — max, где -   любое целое число,   -  длина волны.

Напротив, если вторая волна отстает от первой на нечетное число полуволн, то колебания, вызванные ими, будут происходить в противоположных фазах и волны гасят друг друга.

 — min, где -   любое целое число,   -  длина волны.

Для учета того, что в разных веществах скорость света различна, при определении положений минимумов и максимумов используют не разность хода, а оптическую разность хода. Разность оптических длин пути называется оптической разностью хода.

 — оптическая длина пути,

 — оптическая разность хода.

Если известен радиус кривизны R поверхности линзы, то можно вычислить, на каких расстояниях от точки соприкосновения линзы со стеклянной пластиной разности хода таковы, что волны определенной длины λ гасят друг друга. Эти расстояния и являются радиусами темных колец Ньютона. Необходимо также учитывать тот факт, что при отражении световой волны от оптически более плотной среды фаза волны меняется на , этим объясняется тёмное пятно в точке соприкосновения линзы и плоскопараллельной пластины. Линии постоянной толщины воздушной прослойки под сферической линзой представляют собой концентрические окружности при нормальном падении света, при наклонном — эллипсы. Радиус k-го светлого кольца Ньютона (в предположении постоянного радиуса кривизны линзы) в отражённом свете выражается следующей формулой:

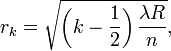
где

R — радиус кривизны линзы;

k = 2, 4, …;

λ — длина волны света в вакууме;

n — показатель преломления среды между линзой и пластинкой.

24)Дифракция света. Метод зон Френеля.

Дифракцией называется огибание волнами препятствий, встречающихся на их пути, или в более широком смысле - любое отклонение распространения волн вблизи препятствий от законов геометрической оптики. Благодаря дифракции волны могут попадать в область геометрической тени, огибать препятствия, проникать через небольшие отверстия в экранах и т. д. Например, звук хорошо слышен за углом дома, т. е. звуковая волна его огибает.

Явление дифракции объясняется с помощью принципа Гюйгенса, согласно которому каждая точка, до которой доходит волна, служит центром вторичных волн, а огибающая этих волн задает положение волнового фронта в следующий момент времени.  

Явление дифракции характерно для волновых процессов. Поэтому если свет является волновым процессом, то для него должна наблюдаться дифракция, т. е. световая волна, падающая на границу какого-либо непрозрачного тела, должна огибать его (проникать в область геометрической тени). Из опыта, однако, известно, что предметы, освещаемые светом, идущим от точечного источника, дают резкую тень и, следовательно, лучи не отклоняются от их прямолинейного распространения. Почему же возникает резкая тень, если свет имеет волновую природу? К сожалению, теория Гюйгенса ответить на этот вопрос не могла.

Принцип Гюйгенса решает лишь задачу о направлении распространения волнового фронта, но не затрагивает вопроса об амплитуде, а следовательно, и об интенсивности волн, распространяющихся по разным направлениям. Френель вложил в принцип Гюйгенса физический смысл, дополнив его идеей интерференции вторичных волн.

Согласно принципу Гюйгенса - Френеля, световая волна, возбуждаемая каким-либо источником S, может быть представлена как результат суперпозиции когерентных вторичных волн, «излучаемых» фиктивными источниками. Такими источниками могут служить бесконечно малые элементы любой замкнутой поверхности, охватывающей источник S. Обычно в качестве этой поверхности выбирают одну из волновых поверхностей, поэтому все фиктивные источники действуют синфазно. Таким образом, волны, распространяющиеся от источника, являются результатом интерференции всех когерентных вторичных волн. Френель исключил возможность возникновения обратных вторичных волн и предположил, что если между источником и точкой наблюдения находится непрозрачный экран с отверстием, то на поверхности экрана амплитуда вторичных волн равна нулю, а в отверстии - такая же, как при отсутствии экрана.

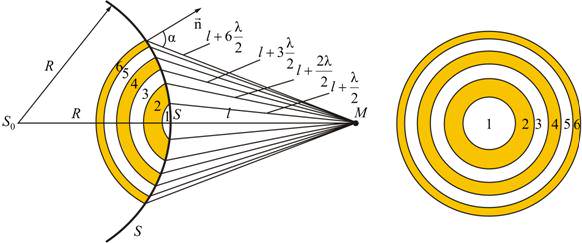
Френель предложил оригинальный метод разбиения волновой поверхности S на зоны, позволивший сильно упростить решение задач (метод зон Френеля).       Границей первой (центральной) зоны служат точки поверхности S, находящиеся на расстоянии  от точки M (рис. 9.2). Точки сферы S, находящиеся на расстояниях , , и т.д. от точки M, образуют 2, 3 и т.д. зоны Френеля.       Колебания, возбуждаемые в точке M между двумя соседними зонами, противоположны по фазе, так как разность хода от этих зон до точки M    . Рис. 9.2       Поэтому при сложении этих колебаний, они должны взаимно ослаблять друг друга:   ,  (9.2.2)         где A – амплитуда результирующего колебания,  – амплитуда колебаний, возбуждаемая i-й зоной Френеля.       Величина  зависит от площади  зоны и угла  между нормалью к поверхности и прямой, направленной в точку M.       Площадь одной зоны .       Отсюда видно, что площадь зоны Френеля не зависит от номера зоны i. Это значит, что при не слишком больших i площади соседних зон одинаковы.       В то же время с увеличением номера зоны возрастает угол  и, следовательно, уменьшается интенсивность излучения зоны в направлении точки M, т.е. уменьшается амплитуда . Она уменьшается также из-за увеличения расстояния до точки M:  .       Общее число зон Френеля, умещающихся на части сферы, обращенной в сторону точки M, очень велико: при , , число зон , а радиус первой зоны .       Отсюда следует, что углы между нормалью к зоне и направлением на точку M у соседних зон примерно равны, т.е. что амплитуды волн, приходящих в точку M от соседних зон, примерно равны.       Световая волна распространяется прямолинейно. Фазы колебаний, возбуждаемые соседними зонами, отличаются на π. Поэтому в качестве допустимого приближения можно считать, что амплитуда колебания  от некоторой m-й зоны равна среднему арифметическому от амплитуд примыкающих к ней зон, т.е. .       Тогда выражение (9.2.1) можно записать в виде   .  (9.2.2)         Так как площади соседних зон одинаковы, то выражения в скобках равны нулю, значит результирующая амплитуда .       Интенсивность излучения   .       Таким образом, результирующая амплитуда, создаваемая в некоторой точке M всей сферической поверхностью, равна половине амплитуды, создаваемой одной лишь центральной зоной, а интенсивность .       Так как радиус центральной зоны мал ( ), следовательно, можно считать, что свет от точки P до точки M распространяется прямолинейно.       Если на пути волны поставить непрозрачный экран с отверстием, оставляющим открытой только центральную зону Френеля, то амплитуда в точке M будет равна . Соответственно, интенсивность в точке M будет в 4 раза больше, чем при отсутствии экрана (т.к. ). Интенсивность света увеличивается, если закрыть все четные зоны.       Таким образом, принцип Гюйгенса–Френеля позволяет объяснить прямолинейное распространение света в однородной среде.       Правомерность деления волнового фронта на зоны Френеля подтверждена экспериментально. Для этого используются зонные пластинки – система чередующихся прозрачных и непрозрачных колец.       Опыт подтверждает, что с помощью зонных пластинок можно увеличить освещенность в точке М, подобно собирающей линзе.