1 Вопрос

Виды колебаний. Свободные (собственные), гармонические колебания и их характеристики.

Колебания-движение периодически повторяющийся процесс во премени.

Свободные (или собственные) — это колебания в системе под действием внутренних сил после того, как система выведена из состояния равновесия (в реальных условиях свободные колебания всегда затухающие

Вынужденные — колебания, протекающие в системе под влиянием внешнего периодического воздействия. Примеры: листья на деревьях, поднятие и опускание руки. При вынужденных колебаниях может возникнуть явление резонанса: резкое возрастание амплитуды колебаний при совпадении собственной частоты осциллятора и частоты внешнего воздействия.

Гармонические колебания — колебания, при которых физическая (или любая другая) величина изменяется с течением времени по синусоидальному или косинусоидальному закону. Кинематическое уравнение гармонических колебаний имеет вид

или

,

где х — смещение (отклонение) колеблющейся точки от положения равновесия в момент времени t; А — амплитуда колебаний, это величина, определяющая максимальное отклонение колеблющейся точки от положения равновесия; ω — циклическая частота, величина, показывающая число полных колебаний происходящих в течение 2π секунд;   — полная фаза колебаний,   — начальная фаза колебаний.

Обобщенное гармоническое колебание в дифференциальном виде

• Амплитуда — максимальное отклонение колеблющейся величины от некоторого усреднённого её значения для системы, 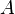  (м)

• Период — промежуток времени, через который повторяются какие-либо показатели состояния системы (система совершает одно полное колебание),   (с)

• Частота — число колебаний в единицу времени, 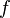  (Гц, с⁻¹).

Период колебаний   и частота   — обратные величины;

 и 

В круговых или циклических процессах вместо характеристики «частота» используется понятие круговая (циклическая) частота   (рад/с, Гц, с⁻¹), показывающая число колебаний за   единиц времени:

2 Вопрос Гармонические колебания. Пружинный маятник

Пружинный маятник – груз массой m, подвешенный на абсолютно упругой пружине и совершающий гармонические колебания под действием упругой силы F=-kx

Для того, чтобы свободные колебания совершались по гармоническому закону, необходимо, чтобы сила, стремящаяся возвратить тело в положение равновесия, была пропорциональна смещению тела из положения равновесия и направлена в сторону, противоположную смещению 

F (t) = ma (t) = –m ω2 x (t).

Рисунок 2.2.1. Колебания груза на пружине. Трения нет

Круговая частота ω₀ свободных колебаний груза на пружине находится из второго закона Ньютона: 

откуда 

Частота ω₀ называется собственной частотой колебательной системы.

Период T гармонических колебаний груза на пружине равен 

При горизонтальном расположении системы пружина–груз сила тяжести, приложенная к грузу, компенсируется силой реакции опоры. Если же груз подвешен на пружине, то сила тяжести направлена по линии движения груза. В положении равновесия пружина растянута на величину x₀, равную 

и колебания совершаются около этого нового положения равновесия. Приведенные выше выражения для собственной частоты ω₀ и периода колебаний T справедливы и в этом случае.

Строгое описание поведения колебательной системы может быть дано, если принять во внимание математическую связь между ускорением тела a и координатой x: ускорение является второй производной координаты тела x по времени t: 

Поэтому второй закон Ньютона для груза на пружине может быть записан в виде 

или 

(*)

где 

Все физические системы (не только механические), описываемые уравнением (*), способны совершать свободные гармонические колебания, так как решением этого уравнения являются гармонические функции вида 

x = xm cos (ωt + φ0).

- груз на пружине при малых отклонениях совершает гармонические колебания во времени t с периодом Т и амплитудой А. - колебания происходят по закону синуса (начинаются от толчка груза) ... - ... или по закону косинуса (начинаются отведением груза в сторону).