2.2 Пересечение поверхности плоскостью (из-1)

При выполнении первого индивидуального задания необходимо определить проекции линии пересечения поверхности плоскостью и построить полученное сечение. Для выполнения задания необходимо увеличить эскиз с рис. 1 «Индивидуального задания» в 3 – 3,5 раза на лист чертежной бумаги формата А3 (предпочтительно вертикального расположения). Пример дан в приложении А. К чертежу задания ИЗ-1 необходимо приложить листок, где в письменной форме кратко изложить формулировку задачи и план ее решения (можно в алгоритмической записи).

Для определения проекций линии пересечения поверхности плоскостью можно воспользоваться одним из способов: методом вспомогательных секущих плоскостей, проводя их через ребра геометрической фигуры (метод ребер) или методом замены плоскостей проекций.

1. Метод вспомогательных секущих плоскостей. Суть этого метода заключается в определении точки пересечения каждого ребра заданной гранной поверхности (пирамиды, призмы) или нескольких образующих линейчатой поверхности вращения (конуса, наклонного цилиндра) с плоскостью (задача на определение точки пересечения прямой общего положения с плоскостью общего положения, см. рис. 5 и 6). Соединив последовательно полученные точки пересечения на соответствующих проекциях с учетом видимости, получаем проекции искомой линии пересечения поверхности и плоскости. На рис. 7 приведен пример применения этого метода для решения задачи на нахождение проекций линии пересечения наклонной призмы плоскостью (f  h) - КLF(K₁L₁F₁, K₂L₂F₂).

Рис. 7

2. Метод замены плоскостей проекций. Суть применения этого метода заключается в преобразовании системы плоскостей проекций так, чтобы заданная секущая плоскость общего положения стала проецирующей плоскостью в новой системе плоскостей проекций (см. рис. 3). Точки пересечения ребер поверхности или образующих линейчатой поверхности вращения с заданной секущей плоскостью однозначно определяются на новой плоскости проекций. По проекциям точек F₄, E₄ и R₄ с учетом принадлежности геометрических элементов (точка F принадлежит ребру SC пирамиды, точка E – ребру SA, точка R – ребру SB) по линиям связи строятся проекции F₁, E₁ и R₁, а затем проекции F₂, E₂ и R₂. Целесообразно делать проверку, а именно: F₄F_x1 = F₂F_x; E₄E_x1 = E₂E_x и R₄R_x1 = R₂R_x. Полученные проекции точек пересечения соединить последовательно с учетом видимости линии, определить видимость поверхности (рис. 8).

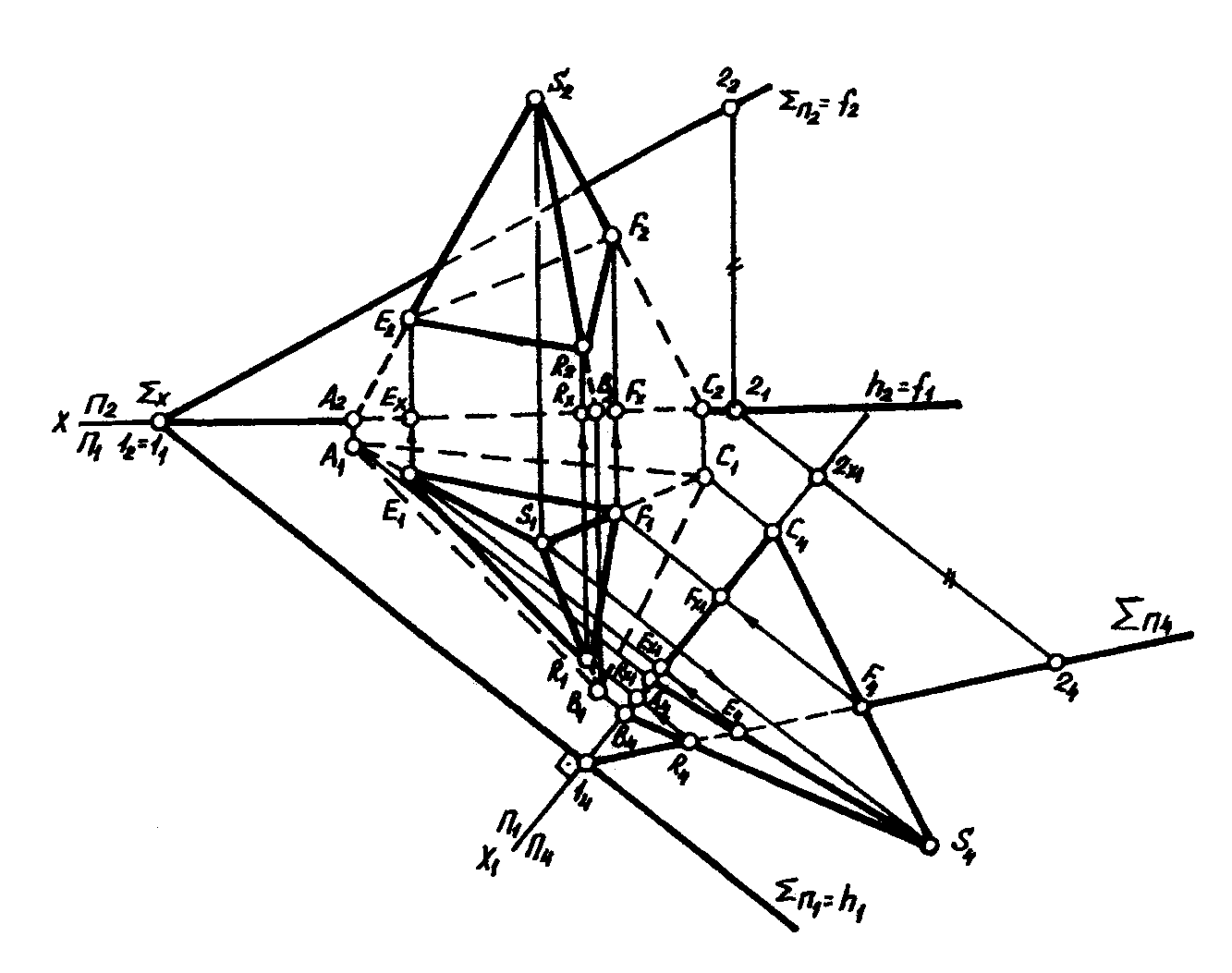
Рис. 8

Для определения натурального вида сечения трехгранной наклонной пирамиды плоскостью можно воспользоваться способом замены плоскостей проекций (см. рис. 4 и приложение А).

2.3 Взаимное пересечение поверхностей

2.3.1 Метод вспомогательных секущих плоскостей

На рис. 9 показано построение линии пересечения поверхностей вращения (конуса и сферы).

Сначала определяются опорные точки линии пересечения: с помощью фронтальной плоскости уровня Ф (след Ф_П1), которая пересекает обе поверхности по их очеркам (по окружности f(f₁, f₂) и 1S2(1₁S₁2₁, 1₂S₂2₂) - отмечаются проекции точек А(А₂), В(В₂): f₂(S₂ – 2₂)=A₂(B₂). Достраиваются горизонтальные проекции точек А(А₁), В(В₁): A₂A₁(B₂B₁)f₁=A₁(B₁). Эти опорные точки являются наивысшей А и наинизшей В точками линии пересечения, а также точками видимости линии на плоскости П₂.

Далее определяются точки видимости линии относительно горизонтальной плоскости П₁, которые находятся путем введения вспомогательной секущей горизонтальной плоскости уровня Г¹, проходящей по экватору сферы h(h₁,h₂). Эта плоскость пересекает конус по окружности радиуса R – параллель h¹(h₁¹,h₂¹). На пересечении h(h₁,h₂) и h¹(h₁¹,h₂¹) определяются проекции точек С и D: h₁  h₁¹ = C₁(D₁); C₁C₂  h₂(h₂¹) = C₂(D₂).

Рис. 9

Промежуточные точки линии пересечения определяются путем введения вспомогательных секущих горизонтальных плоскостей уровня в интервале между точками А и В. При пересечении любой вспомогательной плоскости с заданными поверхностями получаются соответствующие окружности, на пересечении которых и находятся искомые точки линии пересечения. Например, с помощью плоскости Г² определяются проекции точек М и N (M₁ и N₁), с помощью плоскости Г³ определяются проекции точек E и F (Е₁ и F₁). Последовательно соединяя проекции точек C₁, N₁, A₁, M₁ и D₁ (видимая часть проекции линии пересечения), а также D₁, E₁, B₁, F₁ и C₁ (невидимая часть проекции) изображается горизонтальная проекция линии пересечения заданных поверхностей.

Фронтальную проекцию линии пересечения строим по свойству принадлежности найденных точек соответствующим вспомогательным секущим плоскостям. Фронтальные проекции точек С и D принадлежат плоскости Г¹, т.е. С₂  Г₂¹ и D₂  Г₂¹. Аналогично определяются фронтальные проекции точек М и N (M₂  Г₂²; N₂  Г₂²), а также точек Е и F (E₂  Г₂³ и F₂  Г₂³).

Если в условии задачи дан частный случай, когда образующие одной из пересекающихся поверхностей перпендикулярны плоскости проекций, то на этой плоскости проекций линия пересечения совпадает с очерком заданной проецирующей поверхности. Задача сведется к нахождению второй проекции линии пересечения, используя свойство принадлежности точек линии пересечения второй пересекающейся поверхности. На рис. 10 приведен пример построения линии пересечения конуса и цилиндра, образующие которого перпендикулярны плоскости П₂. Опорными точками линии пересечения являются точки А(А₁,А₂) и В(В₁,В₂). Фронтальная проекция линии пересечения определена – совпадает с очерком цилиндра, горизонтальную проекцию строим с помощью вспомогательных секущих горизонтальных плоскостей уровня. В пересечении конуса со вспомогательными секущими плоскостями получаются окружности, в пересечении с цилиндром – прямоугольники. Точки видимости линии относительно плоскости П₁ определяются путем введения вспомогательной секущей плоскости Г¹, проходящей по оси симметрии цилиндра. Плоскость Г¹ пересекает конус по окружности радиуса R¹, цилиндр – по прямоугольнику n(n₁,n₂), на пересечении окружности и n(n₁,n₂) определяются точки С(С₁) и D(D₁). Построение промежуточных точек: с помощью вспомогательной плоскости Г² получаются точки К(К₁) и N(N₁): Г² пересекает конус по окружности радиуса R² и цилиндр по прямоугольнику m(m₁,m₂), на пересечении получаются искомые точки. Для более точного построения задается несколько вспомогательных секущих плоскостей.

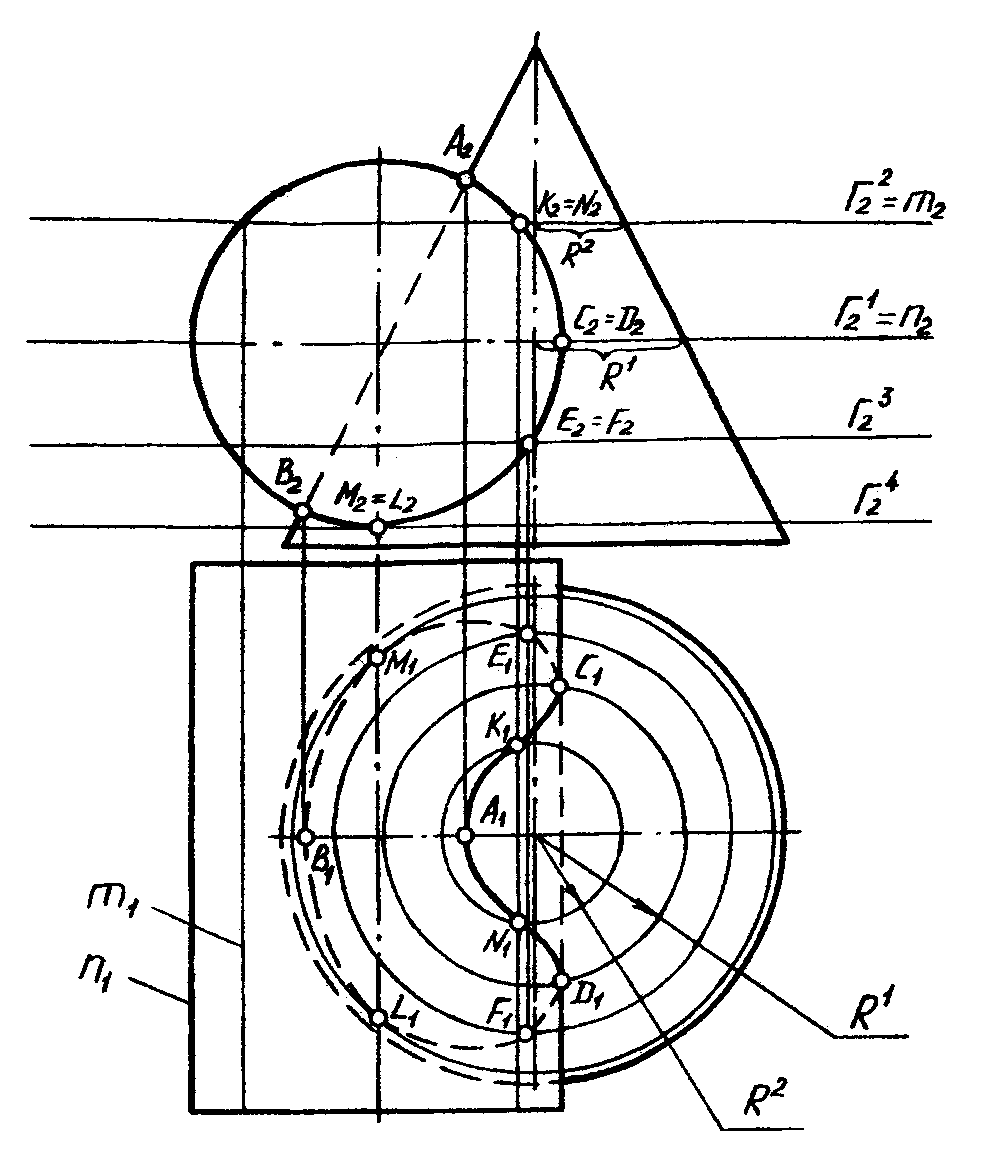
Рис. 10