
- •1Предмет статистики как особой отрасли науки.
- •2Теоретические и методологические основы статистики.
- •3.Основные задачи и функции статистики в переходный период к рыночной экономике
- •4, Виды статистического наблюдения массовых общественных явлений
- •5. Ошибки статистического наблюдения и способы их контроля.
- •6. Понятие сводки статистических данных.
- •7. Сущность группировки статистических данных, задачи, решаемые на её основе.
- •8.Научные основы группировки. Выбор группировочного признака.
- •9.Методика определения величины интервала группировки
- •10. Табличное оформление результатов группировки.
- •12. Виды абсолютных величин, их значение и способы получения.
- •13. Формы выражения и виды относительных величин.
- •14. Область практического применения относительных величин в изучении экономических явлений
- •15. Понятие средних величин, их виды и условия применения.
- •16 Методика расчёта средней арифметической (простой и взвешенной).
- •17. Методика расчёта средней арифметической взвешенной в дискретном и интервальном рядах распределения.
- •18. Методика расчёта средней гармонической и область её практического применения.
- •19. Средняя геометрическая: методика расчёта и область практического применения.
- •20. Методика расчёта моды и медианы и область их практического применения.
- •21. Статистические показатели вариации признаков и их экономический смысл.
- •22. Правило сложения дисперсии.
- •23. Понятие и виды динамических рядов.
- •24. Основные правила построения динамических рядов.
- •28. Статистические методы измерения сезонных колебаний.
- •29. Методика определения среднегодовых темпов роста и прироста.
- •30. Понятие индексов. Индивидуальные и общие индексы.
- •31. Агрегатная форма индексов динамики и правила их построения.
- •32. Методика расчёта средних гармонических и средних арифметических индексов.
- •33. Система индексов. Использование системы индексов в экономическом анализе.
- •34. Влияние изменения структуры на динамику средних величин (система индексов переменного, постоянного состава и индекс структурных сдвигов).
- •35. Особенности построения территориальных индексов.
- •36. Объективная необходимость выборочного наблюдения в рыночной экономике.
- •37. Способы отбора выборочной совокупности
- •38. Ошибки выборочного наблюдения и их классификация.
- •40. Методика расчёта ошибки выборочной доли.
- •41. Методы распространения выборочных данных на генеральную совокупность.
- •42 Область практического применения выборочных исследований в рыночной экономике.
- •43. Виды взаимосвязей экономических явлений и значение их статистического изучения.
- •44, Статистические методы изучения связи между явлениями
- •45. Корреляционный метод в анализе взаимосвязи экономических явлений.
- •46. Определение тесноты связи признаков экономических явлений.
- •47. Использование корреляционного метода в прогнозировании экономических явлений.
- •48. Графический способ изображения статистических данных.
45. Корреляционный метод в анализе взаимосвязи экономических явлений.
При изучении экономических явлений методами К. а. необходимо тщательно выявлять причинные зависимости, лежащие в основе корреляции наблюдаемых показателей. Отсутствие причинной связи между явлениями (хотя корреляционная связь между ними установлена) называется ложной корреляцией. Она часто встречается при анализе временных рядов, когда параллельно снижаются или повышаются показатели, на самом деле совершенно не зависящие друг от друга.
Рассматриваемые связи математически описываются корреляционными уравнениями (другое название — уравнение регрессии). Напр., простейшим корреляционным уравнением связи между двумяпеременными является уравнение прямой вида y = a + bx. При функциональной связи такая прямая точно соответствовала бы всем значениям зависимой переменной. Если представить такую связь графически, то она проходила бы через все наблюдаемые точки y. При корреляции же соответствие, как указано, соблюдается лишь приблизительно, в общем, и точки наблюдений расположены не по прямой, а в виде “облачка”, более или менее вытянутого в некотором направлении. Поэтому приходится специальными приемами находить ту линию, которая наилучшим образом отражает корреляционную зависимость, т. е. направление “облачка” (рис. К. 1). Распространенный способ решения этой задачи — метод наименьших квадратов отклонений наблюдаемых значений y от значений, рассчитываемых по формуле корреляционного уравнения.
Особенно широко применяется К. а. в теории производственных функций, в разработке разного рода нормативов на производстве, а также в анализе спроса и потребления.
46. Определение тесноты связи признаков экономических явлений.
.
К простейшим показателям степени тесноты связи относят коэффициент корреляции знаков, предложенный немецким учёным Г.Фехнером. Этот показатель основан на оценке степени согласованности знаков (направлений) отклонений факторного и результативного признаков от их средних значений.
Коэффициент
корреляции знаков определяется формулой
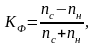 где
где
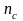 - число совпадений знаков отклонений
индивидуальных величин
- число совпадений знаков отклонений
индивидуальных величин
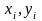 от их средних
от их средних
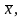 ;
;
 - число несовпадений знаков отклонений.
Коэффициент Фехнера может принимать
значение в пределах от -1 до +1. Если знаки
большинства пар отклонений совпадут,
то тогда показатель будет близок к 1,
что свидетельствует о наличии прямой
связи.
- число несовпадений знаков отклонений.
Коэффициент Фехнера может принимать
значение в пределах от -1 до +1. Если знаки
большинства пар отклонений совпадут,
то тогда показатель будет близок к 1,
что свидетельствует о наличии прямой
связи.
Более совершенным показателем степени тесноты связи является линейный коэффициент корреляции, впервые введённый английским математиком К.Пирсоном:

В этом показателе учитываются не только знаки отклонений индивидуальных значений признаков от средних, но и сами величины таких отклонений.
Между линейным
коэффициентом
и коэффициентом регрессии
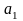 в уравнении линейной парной регрессии
существует зависимость, определяемая
формулой
в уравнении линейной парной регрессии
существует зависимость, определяемая
формулой
 где
где
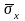 и
и
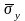 - средние квадратические отклонения
факторного и результативного признаков,
соответственно.
- средние квадратические отклонения
факторного и результативного признаков,
соответственно.
Линейный
коэффициент корреляции имеет большое
значение при исследовании
социально-экономических явлений и
процессов, распределение которых близко
к нормальному. Поэтому на практике часто
анализ начинают с расчёта этого
коэффициента. Линейный коэффициент
корреляции может принимать значения в
пределах от -1 до +1. Чем ближе коэффициент
корреляции по абсолютной величине к 1,
тем теснее связь между признаками. Знак
при коэффициенте корреляции указывает
на направление связи – прямой зависимости
соответствует знак плюс, а обратной –
знак минус. Условие
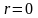 является необходимым и достаточным,
чтобы признаки
и
были независимы. При этом условии
соответствующие коэффициенты регрессии
обращаются в нуль, а прямые регрессии
является необходимым и достаточным,
чтобы признаки
и
были независимы. При этом условии
соответствующие коэффициенты регрессии
обращаются в нуль, а прямые регрессии
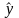 по
и
по
и
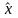 по
оказываются взаимно перпендикулярными
в прямоугольной системе координат.
по
оказываются взаимно перпендикулярными
в прямоугольной системе координат.
Линейный коэффициент корреляции достаточно точно оценивает степень тесноты связи лишь в случае наличия линейной зависимости между признаками. При наличии же криволинейной зависимости линейный коэффициент корреляции недооценивает степень тесноты связи и даже может быть равен нулю. В таких случаях зависимости между признаками применяют эмпирическое корреляционное отношение и теоретическое корреляционное отношение (индекс корреляции).
Эмпирическое
корреляционное отношение
 рассчитывается
по данным, получаемым в результате
группировки
рассчитывается
по данным, получаемым в результате
группировки
 где
где
![]() - общая дисперсия результативного
признака;
- общая дисперсия результативного
признака; - межгрупповая дисперсия результативного
признака;
- межгрупповая дисперсия результативного
признака;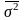 - средняя внутригрупповых дисперсий
результативного признака.
- средняя внутригрупповых дисперсий
результативного признака.
Теоретическое
корреляционное отношение
определяется по формуле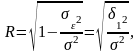
где
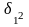 - факторная
дисперсия или
дисперсия выравненных значений
результативного признака (т.е. рассчитанных
по уравнению регрессии)
- факторная
дисперсия или
дисперсия выравненных значений
результативного признака (т.е. рассчитанных
по уравнению регрессии)
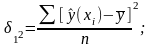
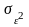 - остаточная
дисперсия,
отображающая вариацию результативного
признака
от всех прочих, кроме
,
факторов
- остаточная
дисперсия,
отображающая вариацию результативного
признака
от всех прочих, кроме
,
факторов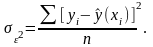 Соотношение между факторной
и общей
дисперсиями
Соотношение между факторной
и общей
дисперсиями
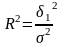 называется индексом
детерминации и
характеризует часть общей вариации
результативного признака
,
описываемую фактором
в регрессионной модели. Корень квадратный
из индекса детерминации определяет
индекс
корреляции
называется индексом
детерминации и
характеризует часть общей вариации
результативного признака
,
описываемую фактором
в регрессионной модели. Корень квадратный
из индекса детерминации определяет
индекс
корреляции
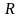 .
.
Представленные
выше показатели тесноты связи, исчисленные
по данным сравнительно небольшой
статистической совокупности (при
 ),
могут искажаться действием случайных
причин. Это вызывает необходимость
проверки их существенности.
),
могут искажаться действием случайных
причин. Это вызывает необходимость
проверки их существенности.
Для оценки
значимости коэффициента корреляции
(или коэффициентов регрессии) применяется
t
–критерий Стьюдента.
Вычисленное значение
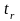 критерия
критерия
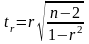
сравнивается с
критическим
 ,
которое берётся из таблицы значений
Стьюдента с учётом заданного уровня
значимости
,
которое берётся из таблицы значений
Стьюдента с учётом заданного уровня
значимости
 и числа степеней свободы
и числа степеней свободы
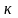 .
Если величина
.
Если величина
 ,
то величина коэффициента корреляции
признаётся значимой.
,
то величина коэффициента корреляции
признаётся значимой.
Для оценки
значимости индекса корреляции
(или адекватности построенной
регрессионной модели) применяется
F-критерий
Фишера.
Фактическое значение критерия
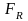 вычисляется по формуле
вычисляется по формуле
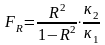
и сравнивается с
критическим значением
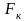 ,
которое определяется по таблице
F-критерия
с учётом принятого уровня значимости
и числа степеней свободы
,
которое определяется по таблице
F-критерия
с учётом принятого уровня значимости
и числа степеней свободы
 и
и
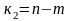
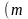 - число параметров уравнения регрессии).
При
- число параметров уравнения регрессии).
При
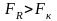 величина индекса корреляции признаётся
значимой.
величина индекса корреляции признаётся
значимой.
В случаях, если изучаются совокупности достаточно большого объёма, применяют другие методы оценки значимости описанных выше показателей (например, пользуются таблицей интеграла вероятностей Лапласа).
В заключение настоящей темы следует подчеркнуть, что интерпретация моделей регрессии должна осуществляться методами той отрасли знаний, к которой относятся исследуемые явления и процессы. Но всякая интерпретация начинается со статистической оценки уравнения регрессии в целом и оценки значимости входящих в модель параметров.
При анализе адекватности уравнения регрессии описываемому процессу возможны следующие варианты:
1) построенная модель на основе её проверки по F-критерию в целом адекватна, и все коэффициенты регрессии значимы. Такая модель может быть использована для принятия решений и прогнозов;
2) модель по F-критерию адекватна, но часть коэффициентов регрессии незначима. В этом случае модель пригодна для принятия некоторых решений, но не для производства прогнозов;
3) модель по F-критерию адекватна, но все коэффициенты регрессии незначимы. Такая модель непригодна для принятия решений и осуществления прогнозов.
