40. Методика расчёта ошибки выборочной доли.
Ошибка выборки в статистике это некоторая средняя величина или обобщающая
характеристика, ошибок полученных при многократном повторении испытаний.
W
- P
-
ошибка выборки;
-
выборочная средняя;
-
генеральная средняя;
W – доля единиц, обладающих изучаемым признаком в выборочной совокупности
(выборочная доля);
P - доля единиц, обладающих изучаемым признаком в генеральной совокупности.
Величина ошибок зависит от способа отбора. В математической статистике доказано,
что средняя ошибка выборки (математическое ожидание средней ошибки
выборки) – это среднеквадратическое отклонение распределения выборочной средней
величины.
Ошибка выборки определяется:
В
математической статистике доказано,
что средняя ошибка собственно случайного
повторного отбор рассчитывается:
, где
-
средняя ошибка выборки;
-
дисперсия генеральной совокупности;
-
численность выборки.Если исследуется
выборочная доля при повторном отборе
,
где
- дисперсия
биномиального распределения.
Результаты повторного отбора подчиняются закону биномиального распределения.
При бесповторном отборе результаты многократной выборки и распределения ошибок
подчиняются гипергеометрическому распределению, и формула средней ошибки имеет
вид:
,
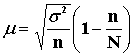соответственно
для выборочной доли
.При
выборках большой численности, когда
из массовых генеральных совокупностей
(
)
для расчета ошибок выборки можно
использовать формулу повторного отбора.
В формулах средней ошибки выборки присутствует генеральная дисперсия. Однако,
она, как правило, неизвестна. Если мы проводим выборку для того, чтобы
изучить только часть совокупности, мы не можем знать генеральную дисперсию.
Исключение составляют только выборки, проводимые для контроля результата
сплошного наблюдения.
41. Методы распространения выборочных данных на генеральную совокупность.
Для получения характеристик генеральной совокупности по соответствующим показателям выборки в зависимости от цели исследования применяется:
а) способ прямого пересчёта показателей выборки;
б) способ поправочных коэффициентов.
Способ прямого
пересчёта состоит
в том, что показатели выборочной
совокупности (
или
)
распространяются на генеральную
совокупность с учётом предельной ошибки
выборки (
или
).
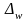Средняя
характеристика количественного признака
по генеральной совокупности при
известных значениях средней характеристики
признака
по выборке и предельной ошибки выборки
определяется по формуле
Для установления
пределов, в которых находится доля
альтернативного признака в генеральной
совокупности
по известной доле признака в выборочной
совокупности
и известному значения предельной
ошибки выборки
применяется формула
Способ поправочных коэффициентов применяется в случаях, когда целью выборочного метода является проверка или уточнение результатов сплошного наблюдения.
В статистической практике этот способ используется при уточнении данных переписей имущества, животных в домашних хозяйствах и др. Например, если в хозяйствах населения деревни по данным 10%-ной выборки было зарегистрировано 104 головы скота, а по более ранним данным сплошного учёта в этом массиве значится 100 голов, то коэффициент недоучёта составляет (104 – 100)/100=0,04 (или 4%).
С учётом этого коэффициента вносится поправка в общую численность скота.