37. Способы отбора выборочной совокупности

Способы отбора единиц, применяемые в практике выборочного метода исследования, определяются правилами формирования выборочной совокупности, в зависимости от которых выборка может быть:

1) собственно-случайная – состоит в том, что выборочная совокупность получается в результате случайного отбора отдельных единиц из генеральной совокупности. Количество единиц выборки определяется исходя из принятой доли выборки. Примерами такой выборки может служить розыгрыш спортлото, жеребьёвка и т.д.;

2) механическая – состоит в том, что отбор единиц в выборку производится из генеральной совокупности, разбитой на равные интервалы (группы). Размер интервала в генеральной совокупности принимается равным обратной величине доли выборки. Так, при 5%-ной выборке механически (подряд) отбирается каждая 20-я единица. По способу проведения механический отбор всегда бесповторный;

3) типическая – состоит в том, что генеральная совокупность вначале расчленяется на однородные типические группы, затем из каждой типической группы собственно-случайной или механической выборкой производится индивидуальный отбор единиц в выборочную совокупность. Отбор единиц может быть пропорциональным удельному весу каждой группы или непропорциональным. Типическая выборка применяется при изучении сложных статистических совокупностей. Например, при выборочном обследовании производительности труда работников, состоящих из отдельных групп по квалификации. Типическая выборка даёт более точные результаты по сравнению с другими способами отбора единиц, что обеспечивается расчленением генеральной совокупности на качественно однородные группы и представительством в выборке (репрезентативностью) каждой типологической группы;

4) серийная (гнездовая) – состоит в том, что из генеральной совокупности отбираются не отдельные единицы, а целые их серии (гнёзда), причём внутри каждой серии обследуются все без исключения единицы. Серии могут быть как равновеликие, так и неравновеликие по численности;

5) комбинированная – заключается в том, что одновременно используются (комбинируются) несколько предыдущих способов отбора. Например, серийный отбор сочетается с собственно-случайным.

При организации выборочного наблюдения следует иметь ввиду, что размер ошибки выборки прежде всего зависит от численности выборочной совокупности . Из формулы для ошибки выборки 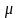видно, что средняя ошибка выборки обратно пропорциональна , то есть при увеличении численности выборки, например, в 9 раз, ошибка выборки уменьшается только в 3 раза.

38. Ошибки выборочного наблюдения и их классификация.

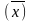Возможные расхождения между характеристикой выборочной и генеральной совокупности измеряются средней ошибкой выборки . В математической статистике доказывается, что значения средней ошибки выборки определяются по формуле

где n - численность единиц выборки, 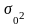- дисперсия генеральной совокупности. Генеральная дисперсия на практике, как правило, неизвестна, поэтому для определения средней ошибки используется дисперсия выборочной совокупности 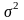. Соотношение между дисперсиями в генеральной и выборочной совокупности имеет вид

При достаточно большом значении n выполняется равенство поэтому для оценки средней ошибки выборки применяется формула

Эта оценка справедлива при повторном отборе единиц совокупности, который предполагает, что каждая зарегистрированная единица выборочной совокупности или их серия после обследования снова возвращаются в генеральную совокупность и в дальнейшем могут быть отобраны повторно.

При бесповторном отборе оценка средней ошибки выборки

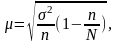
где N - численность единиц генеральной совокупности. Бесповторное проведение отбора предполагает, что отобранная единица в генеральную совокупность не возвращается и в дальнейшем не может подвергаться повторному обследованию.

Дисперсия количественного признака в выборке определяется известной формулой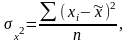

где , - значения признака у отдельных единиц и среднее значение признака в выборочной совокупности.

Дисперсия альтернативного признака в выборочной совокупности для показателя доли признака определяется по формуле

.

Альтернативным признаком называют признак, который может принимать только два значения.

Получаемые значения средней ошибки выборки позволяет определить одно из возможных значений средней величины количественного признака в генеральной совокупности

и одно из возможных значений, в пределах которых может находиться доля альтернативного признака во всей совокупности .

В математической статистике доказывается, что пределы значений характеристик генеральной совокупности и p) отличаются от характеристик выборочной совокупности и на величину 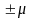лишь с вероятностью 0,683. Вероятность правильности суждений можно повысить, если расширить пределы отклонений, приняв в качестве меры среднюю ошибку выборки, увеличенную в раз. Например, при удвоенном значении вероятность правильного суждения достигает 0,954, а при утроенном – 0,997.

Предельную ошибку выборки находят по формуле ,

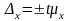где - коэффициент доверия. Величина определяется по специальным таблицам в зависимости от заданного значения доверительной вероятности F. Например, при величине требуемой доверительной вероятности коэффициент доверия

39. Методика расчёта ошибки выборочной средней.

Возможные расхождения между характеристикой выборочной и генеральной совокупности измеряются средней ошибкой выборки . В математической статистике доказывается, что значения средней ошибки выборки определяются по формуле

где n - численность единиц выборки, - дисперсия генеральной совокупности. Генеральная дисперсия на практике, как правило, неизвестна, поэтому для определения средней ошибки используется дисперсия выборочной совокупности . Соотношение между дисперсиями в генеральной и выборочной совокупности имеет вид

При достаточно большом значении n выполняется равенство поэтому для оценки средней ошибки выборки применяется формула

Эта оценка справедлива при повторном отборе единиц совокупности, который предполагает, что каждая зарегистрированная единица выборочной совокупности или их серия после обследования снова возвращаются в генеральную совокупность и в дальнейшем могут быть отобраны повторно.

При бесповторном отборе оценка средней ошибки выборки

где N - численность единиц генеральной совокупности. Бесповторное проведение отбора предполагает, что отобранная единица в генеральную совокупность не возвращается и в дальнейшем не может подвергаться повторному обследованию.