32. Методика расчёта средних гармонических и средних арифметических индексов.

Одной из форм выражения общих индексов являются средние индексы: средний арифметический взвешенный индекс и средний гармонический взвешенный индекс.

Средний арифметический индекс строится таким образом, что он тождественен агрегатным индексам экстенсивных объёмных показателей. Так, например, агрегатный индекс физического объёма преобразуется в средний арифметический взвешенный индекс физического объёма (с учётом, что

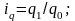
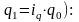
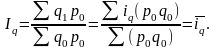
Средний гармонический индекс является преобразованной формой агрегатных индексов качественных интенсивных показателей (цен, себестоимости единицы продукции, производительности труда работника и др.) Например, агрегатный индекс цен преобразуется в формулу гармонического взвешенного индекса цен (с учётом, что ):

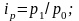
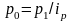33. Система индексов. Использование системы индексов в экономическом анализе.

Системой индексов называется ряд последовательно построенных индексов. Такие системы характеризуют изменения, происходящие в течение интервала времени, включающего в себя более двух периодов. В зависимости от базы сравнения системы индексов бывают: базисными и цепными.

Система базисных индексов — это ряд последовательно вычисленных индексов одного и того же явления с постоянной базой сравнения. Т.е. в знаменателе всех индексов находится индексируемая величина базисного периода.

Система цепных индексов — это ряд индексов, вычисленных с меняющейся от индекса к индексу базой сравнения.

Индексы применяются для характеристики изменения уровня сложных экономических показателей. Их можно использовать также в аналитических целях для оценки влияния на результативный показатель изменения факторов, его формирующих. Предпосылкой для проведения анализа в индексной форме является возможность представления результативного экономического показателя произведением двух или более определяющих его величину показателей или суммой таких произведений.

Оценивать роль отдельных факторов изменения результативного показателя можно путем построения системы взаимосвязанных индексов. Задача состоит в том, что бы рассчитать изменение сложного показателя при изменении величины только одного фактора так, чтобы величина других факторов была бы сохранена на определенном постоянном уровне. В основе приема аналитических индексных расчетов лежит принцип элиминирования (устранения влияния) изменений величины всех факторов, кроме изучаемого. При построении индексов, оценивающих влияние отдельных факторов на изменение сложного показателя, необходимо иметь в виду, что общий результат изменения этого показателя представляет собой сумму изменения за счет влияния всех исследуемых факторов, формирующих этот показатель.

В связи с этим, стоит рассмотреть индекс структурных сдвигов. Под индексом структурных сдвигов понимают индекс, характеризующий влияние изменения только структуры изучаемого явления на динамику среднего уровня этого явления.

Между всеми вышеперечисленными индексами существуют взаимосвязи:

взаимосвязь между индивидуальными и сводными индексами позволяет разложить общее изменение анализируемого показателя на индивидуальные.

взаимосвязь базисных и цепных индексов с постоянными весами позволяет разложить изменение изучаемого показателя за длительный период на изменения более краткого периода.

индекс переменного состава может быть разложен на два индекса: индекс фиксированного состава (изменение только исследуемого показателя), индекс структурных сдвигов (влияние изменения весов на среднее изменение исследуемого показателя).

если экономические показатели связаны между собой как произведение, то их индексы взаимосвязаны точно так же.