22. Правило сложения дисперсии.

В математической статистике доказывается правило сложения дисперсий, которое говорит, что общая дисперсия равна сумме межгрупповой дисперсии и средней внутригрупповых дисперсий. Оно записывается в виде формулы

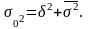
Это правило (закон) сложения дисперсий имеет большую практическую значимость, так как позволяет выявить зависимость вариации от определяющих её факторов при помощи соотношения межгрупповой и общей дисперсии

Это соотношение называется коэффициентом детерминации и определяет процент различий (отклонений) в совокупности, обусловленный признаком-фактором, выбранным для группировки в качестве основного.

Пример. При исследовании производительности труда однородной совокупности рабочих на предприятии была проведена группировка рабочих по размеру заработной платы. В результате статистической обработки данных и расчётов оказалось, что коэффициент детерминации Это означает, что различие в производительности труда отдельных рабочих лишь на 43 % обусловлены фактором заработной платы и, следовательно, на 57 % - остальными факторами (условиями).

В статистике наряду с дисперсией количественного признака определяется дисперсия альтернативного признака. Альтернативными являются признаки (в том числе качественные), которыми обладают одни единицы изучаемой совокупности и не обладают другие. Формула расчёта дисперсии альтернативного признака имеет вид

где 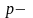доля вариантов, обладающих изучаемым признаком.

23. Понятие и виды динамических рядов.

Рядом динамики называются расположенные в хронологической последовательности статистические показатели, отображающие развитие изучаемого явления во времени.

Каждый ряд динамики содержит два основных элемента:

1) показатели времени t;

2) соответствующие им уровни развития изучаемого явления .

В качестве показаний времени в рядах динамики выступают:

а) либо определённые даты (моменты) времени;

б) либо определённые периоды (интервалы - годы, кварталы, месяцы, сутки).

Уровни рядов динамики могут выражаться абсолютными, относительными или средними величинами.

В зависимости от характера изучаемого явления уровни рядов динамики могут относиться или к определённым датам (моментам) времени или к отдельным периодам. В соответствии с этим ряды динамики по виду подразделяются на: а) моментные; б) интервальные.

Моментные ряды динамики отображают уровни динамического ряда на дату. Примером моментного ряда может быть показатель списочной численности работников предприятия в 2003г. (табл.15).

Табл.15. Списочная численность работников

Дата	1.01 2003г.	1.07 2003г.	1.10 2003г.	31.12 2003г.
Число работников, чел.	164	172	183	179

Особенностью моментного ряда является то, что в его уровни могут входить одни и те же единицы изучаемой совокупности. В представленном примере основная часть персонала предприятия, составляющая списочную численность на 1.01.2003г., продолжая работать в течение года, отображена в последующих уровнях численности. Поэтому при суммировании уровней моментного ряда динамики может возникнуть повторный счёт.

Посредством моментных рядов динамики изучают состояние явления на отдельные даты (моменты) времени (численность работников, товарные запасы, количество оборудования и другие показатели).

Интервальные ряды динамики отображают итоги развития изучаемых явлений за отдельные периоды (интервалы) времени. Например, данные о розничном товарообороте магазина в 1998–2003г.г. приведены в табл.16 в виде интервального ряда.

Табл.16. Розничный товарооборот магазина в 1998–2003г.г.

Год	1998	1999	2000	2001	2002	2003
Объём розничного товарооборота, млн.руб.	724,5	768,7	815,4	903,1	985,3	1012,5

Отличительной особенностью интервальных рядов динамики абсолютных одноимённых величин является возможность суммирования их уровней. Поэтому каждый уровень интервального ряда динамики может складываться из данных за более короткие интервалы (субпериоды) времени. Например, суммирование товарооборота четырёх кварталов, даёт объём товарооборота за год и т.д. Свойство суммирования уровней за последовательные интервалы времени позволяет получать ряды динамики более укрупнённых периодов.

Посредством интервальных рядов динамики в экономике изучается изменение во времени производства, реализации товаров, издержек обращения и других показателей, отображающих итоги развития (функционирования) изучаемого явления за отдельные периоды времени.

Статистическое отображение развития явления во времени может быть также представлено рядами динамики с нарастающими итогами. Их применение обусловлено потребностями отображения результатов развития показателей не только за данный период, но и с учётом предшествующих периодов. При составлении таких рядов производится последовательное суммирование смежных уровней. Например, в табл.17 в виде небольшого ряда динамики с нарастающими итогами представлен розничный товарооборот магазина в 2003г. Данные последней графы отображают обобщённые с начала года результаты по товарообороту по отдельным периодам квартального цикла работы.

Табл.17. Ход изменения розничного товарооборота в 2003г.

Квартал	Розничный товарооборот, млн.руб.
	За квартал	С начала года
Первый Второй Третий Четвёртый	246,2 205,1 256,7 304,5	246,2 451,3 (246,2 + 205,1) (451,3 708 (451,3 + 256,7) 1012,5 (708 + 304,5 )

По виду показателя уровня ряды динамики подразделяются на следующие:

1) ряды динамики абсолютных величин 2) ряды динамики относительных величин; 3) ряды динамики средних величин.