18.Модельное ура-е регрессии…….
Корреляционной зависимостью между двумя переменными величинами называется функциональная зависимость между значениями одной из них и условным математическим ожиданием другой.
Корреляционная зависимость может быть представлена в виде:
Мх(Y)=φ(x) (1) или МY(X)=φ(y) (2)
Уравнения (1) и (2) называются модельными уравнениями регрессии (или просто уравнениями регрессии) соответственно Y по X и X по Y, функции φ(х) и ψ(у) - модельными функциями регрессии (или функциями регрессии), а их графики — модельными линиями регрессии (или линиями регрессии).
Для
точного описания уравнения регрессии
необходимо знать условный закон
распределения переменной
при условии, что переменная
примет значение
,
.
В
статистической практике такой информации
получить не удается, т.к. обычно имеется
выборка пар значений
объема
.
В этом случае речь может идти о приближенном выражении, аппроксимации по выборке функции регрессии. Такой оценкой является выборочная линия (кривая) регрессии
-
условная средняя переменной
при фиксированном значении
,
-
параметры кривой.
При
должна сходиться по вероятности к
функции регрессии
.
Таким образом, эконометрическая модель имеет вид:
где - наблюдаемое значение зависимой переменной,
- объясненная часть, зависящая от значений объясняющих переменных,
- случайная составляющая.
В
многомерном случае, когда х – вектор,
,
где
- могут считаться как случайными, так
и детерминированными.
.
Итак,
чтобы получить достаточно достоверные
и информативные данные о распределении
какой-либо случайной величины, необходимо
иметь выборку её наблюдений достаточно
большого объема. Такие выборки представляют
собой наборы значений
-
число наблюдений,
-
количество объясняющих переменных.
Рассмотрим
.
Парная
регрессия – уравнение связи двух
переменных
.
Определение. Любое эконометрическое исследование начинается со спецификации модели, т.е. с формулировки (выбора) вида модели, исходя из соответствующей теории связи между переменными.
Различают линейные и нелинейные регрессии. Нелинейные регрессии делят на два класса: регрессии, нелинейные относительно включенных объясняющих переменных, но линейных по оцениваемым параметрам, и, регрессии, нелинейные по оцениваемым параметрам.
Линейная:
.
Нелинейные по объясняющим параметрам:
Регрессии, нелинейные по оцениваемым параметрам:
Степенная:
Показательная:
Экспоненциальная:
Логарифмическая:
Полулогарифмическая:
Обратная:
Если
у нас есть набор значений двух переменных
и
то на плоскости
эти значения можно отобразить точками,
таким образом получаем поле
корреляции, которое
изображено на рис. 1.
Рис.1. Поле корреляции
20.Общая дисперсия измеряет вариацию признака по всей совокупности в целом под влиянием всех факторов, обуславливающих эту вариацию. Она равняется среднему квадрату отклонений отдельных значений признака х от общего среднего значения х и может быть определена как простая дисперсия или взвешенная дисперсия.
Внутригрупповая дисперсия характеризует случайную вариацию, т.е. часть вариации, которая обусловлена влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки. Такая дисперсия равна среднему квадрату отклонений отдельных значений признака внутри группы X от средней арифметической группы и может быть вычислена как простая дисперсия или как взвешенная дисперсия.
Таким образом, внутригрупповая дисперсия измеряет вариацию признака внутри группы и определяется по формуле:
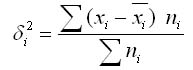
где хi — групповая средняя; ni — число единиц в группе.
Например, внутригрупповые дисперсии, которые надо определить в задаче изучения влияния квалификации рабочих на уровень производительности труда в цехе показывают вариации выработки в каждой группе, вызванные всеми возможными факторами (техническое состояние оборудования, обеспеченность инструментами и материалами, возраст рабочих, интенсивность труда и т.д.), кроме отличий в квалификационном разряде (внутри группы все рабочие имеют одну и ту же квалификацию).
Средняя из внутри групповых дисперсий отражает случайную вариацию, т. е. ту часть вариации, которая происходила под влиянием всех прочих факторов, за исключением фактора группировки. Она рассчитывается по формуле:
Межгрупповая дисперсия характеризует систематическую вариацию результативного признака, которая обусловлена влиянием признака-фактора, положенного в основание группировки. Она равняется среднему квадрату отклонений групповых средних от общей средней. Межгрупповая дисперсия рассчитывается по формуле:
