1.Эконом.Вопросы,приводящие к задачам эконометрики.

Эконометрикой называется наука, позволяющая анализировать связи между различными экономическими показателями на основании реальных статистических данных с применением методов теории вероятностей и математической статистики. С помощью эконометрики выявляют новые, ранее неизвестные связи, уточняют или отвергают гипотезы о существовании определенных связей между экономическими показателями, предлагаемые экономической теорией.

Основная цель эконометрики заключается в модельном описании конкретных количественных взаимосвязей, обусловленных общими качественными закономерностями, выявленными в экономической теории.

Основной предмет исследования эконометрики – это массовые экономические явления и процессы. Предметы исследования эконометрики и статистики являются весьма схожими, потому что эконометрика исследует массовые экономические явления и процессы, а статистика исследует массовые явления и процессы любой природы (в том числе и экономические).

3.Постановка задачи нахождения регрессионной зависимости между величинами по их наблюденным значениям.Корреляционное поле.

Постановка задачи регрессионного анализа формулируется следующим образом .

Имеется совокупность результатов наблюдений. Требуется: установить количественную взаимосвязь между показателем и факторами. В таком случае задача регрессионного анализа понимается как задача выявления такой функциональной зависимости y^* = f(x₂ , x₃ , …, x_т), которая наилучшим образом описывает имеющиеся экспериментальные данные.

Допущения:

• количество наблюдений достаточно для проявления статистических закономерностей относительно факторов и их взаимосвязей;

• обрабатываемые ЭД содержат некоторые ошибки (помехи), обусловленные погрешностями измерений, воздействием неучтенных случайных факторов;

• матрица результатов наблюдений является единственной информацией об изучаемом объекте, имеющейся в распоряжении перед началом исследования.

Функция f(x₂ , x₃ , …, x_т), описывающая зависимость показателя от параметров, называется уравнением (функцией) регрессии. Термин "регрессия" (regression (лат.) – отступление, возврат к чему-либо) связан со спецификой одной из конкретных задач, решенных на стадии становления метода, и в настоящее время не отражает всей сущности метода, но продолжает применяться.

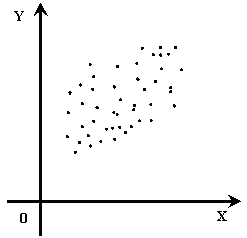
Корреляционным полем называется множество точек {X_i, Y_i} на плоскости XY

Рисунок 6.3 – Пример корреляционного поля (положительная корреляция)	Рисунок 6.4 – Пример корреляционного поля  (отрицательная корреляция)

Если точки корреляционного поля образуют эллипс, главная диагональ которого имеет положительный угол наклона ( / ), то имеет место положительная корреляция (пример на рисунке 6.3).

Если точки корреляционного поля образуют эллипс, главная диагональ которого имеет отрицательный угол наклона ( \ ), то имеет место отрицательная корреляция (пример на рисунке 6.4).

Если же в расположении точек нет какой-либо закономерности, то говорят, что в этом случае наблюдается нулевая корреляция.