1). Общая задача курса МПМ – содействовать улучшению качества методической подготовки студентов к осуществлению математического развития ребенка мл. школьного возраста. Методика( дидактика или педагогика М) – раздел педагогики исслед- й законом-ти обуч. М на опред. уровне ее развития в соотв-и с целями обучения поставленными обществом. ММ призвана дать ответы на 3 главных вопроса: Зачем обучать? какова цель обучения, нужно ли это, если нужно, то зачем. Чему обучать? Какому содержанию обучать, каков должен быть список математических понятий, предназнач-х для изучения, есть критерии отбора содержания, иерархия его построения и чем она обусловлена. Как обучать? какие методы ,приемы, ср-ва, формы обучения следует отбирать и применять для лучшего усвоения ребенком отобранного содержания, как учитывать при обучении психологические особенности возраста и индивидуальные различия детей но в то же время «укладываться» в отведенное время. Впервые ММ возникла в трудах Генриха Пестолоцци 1803 «Наглядное учение о числе». Источники развития ММ: передовой пед. опыт, лабораторный и естественный эксперимент, новые направления в науке математике, научные исследования по педагогике и психологии. Перед ММ стоят конкретные задачи: 1). отбор материала для изуч. в нач школе. 2). разработка школьн. программ. 3). установление наиболее эффект. методов, приемов и ср-в обучения и воспитания. 4). орг-я работы уч-ся по изучению отобраннго материала. Решение этих задач сост-т содержание преподавания ММ в нач.класах. Обьект – процесс обучения математике, в кот. можно выделить 4 компонента: цель, содержание, деятельность учителя и ученика. Предметом может являться любой из названных компонентов, а т.ж. те взаимосвязи кот. есть между ними. След-но, ММ это наука кот. с обной стороны обращена к конкретному содержанию, отбору и упорядочению его в соот-и с целями обучения, а с др. к деятельности учителя и ученика, к процессу усвоения этого содержания. В дисциплине ММ условно можно выделить 3 раздела: 1- общая методика преподавания(изучение методов, ср-в деятельности, построение уроков, знакомство с программами и т.д.). 2 – специальные методы преподавания (изуч. ф-й геометрич. фигур, цифр и т.д.). 3- конкретные методы преподавания математики кот. сост. из частных ? общей и специальной методики. Методическая система обуч. матемаитке включ. в себя ряд взаимосвязанных элементов, важнейш. из кот. явл. цели. +ср-ва обучения, методы обучения, содержание, формы орг. деятельности. (см. схему в тетради). Содержание математического образования: арифметика(нумерация, действия и т.д.), величины (понятие величины, длина, масса и т.д.), геометрия (первонач. представл. о плоскостных фигурах), алгебра (выражения, //-// с переменными, равенства/неравенства, тождества), текстовые (арифметические) задачи, процессы, элементы логики и комбинаторики. Система построения курса см. в тетради.

2). ММ использует осн. идеи, теор. положения и рез-ты исследования др. наук. Н-р, идеи психологии и рез-ты ее исследований использ. методикой для обоснования содержания обучения и последовательности его изучения, для разработки систем упражнений. Идеи физиологии и 2-х сигнальных системах, возрастных этапах созревания подкорковых зон мозга помогают понять механизмы преобретения умений, навыков в процессе обучения. Методика творчески заимствует методы исследований ,прим-х в др. науках. Н-р, из педагогики и психологии методика заимствует метод наблюдения, анкетирования, беседы; из математики статистического анализа. Методика использует конкретные результаты исследований психологии, физиологии ВНД, математики и др. наук. Н-р, рез-ты исследования Ж.Пиаже процесса восприятия детьми мл.школьного возраста сохранение количества породили целые серии конкретных математических заданий в различн. программах для мл.школьников: на спец. построенных упражнениях ребенка учат понимать, что измение формы предмета не влечет за собой изменения его количества (переливание воды). Методика участвует в комплексных исследованиях развития ребенка в процессе его обучения и воспитания. Н-р, в 1980-2002 появился целый ряд научных исследований процесса личностного развития ребенка младшего школьного возраста в ходе обучения его математике. Обобщая вопрос о связи можно сделать о том, что: нельзя вывести из какой-то одной науки систему методических знаний и технологии; данные др. наук необходимы для методических разработок; методика находится в постоянном развитии; методика не просто заимствует и использует данные др. наук, но и интерпретирует их для оптимальной организации учебного процесса.

3). примерный план урока:

1). Появление нового числа путем прищитывания единицы ( с помощью фигурок).

2). Наблюдение за равномощными множествами.

3). Знакомство с числом и цифрой.

4). каллиграфия

5). Возвращение к порядковому и количественному числу с помощью спец. упражнений (н-р, нарисуй 3 круга, а закрась второй).

6). работа по развитию интеллектуальных умений уащихся.

7). Ф-и св-в натурального ряда чисел.

8). Итог о получении числа (2-мя способами: прищитывание и отщитыванием).

Начиная с числа 2 25% урока отводится на изучение состава числа. В процессе работы дети должны усвоить правила счета: начинать считать можно с любого предмета и ни один предмет нельзя пропускать или считать дважды.

4). В советском союзе была принята жесткая цензура школьных программ. Учителям было разрешено работать только по тем учебникам, которые были утверждены и рекомендованы Министерством образования. В 1968 был объявлен конкурс на написание учебника по математике для начальной школы и из всех предложенных был выбран и утвержден учебник, написанный авторским коллективом под руководством М.А.Бантовой и М.И.Моро. Этот учебник стал называться традиционным. Долгие годы он был единственным учебником по математике. Это позволяло создать единое образовательное пространство на все территории бывшего СССР. С одной стороны это было удобно, поскольку не возникало никаких проблем в связи с переездами. Но с др. стороны это приводило к унификации образовательного процесса, при которой учитель был ориентирован главным образом на достижение каждым ребенком определенного уровня учебных норм и требований. После развала СССР стали публиковаться учебники др. авторов, эти учебники стали называться «альтернативными». Некоторые из них были написаны еще в 70-е годы 20 века ( система Занкова, Давыдова и др.), другие изданы в 90-е ( учебники Виленкина и Петерсон, Истоминой и др.). А.М.Пышкало отмечает, что традиционный курс математики для нач. школы характеризуется определенной последовательностью изучаемых базисных понятий: Число → Величина. Основное внимание в нем сосредоточено на выработке навыков письменных вычислений и на их применение в решение текстовых задач. Та же последовательность изучаемых понятий характерна и для альтернативных курсов (учебники системы Занкова, Истоминой и др.). Однако основная направленность методики обучения математики в этих системах другая: ее цель -интеллектуальное развитие ребенка. Как отмечает Истомина, не смотря на то, что в принципе любое обучение развивает ребенка, но при сравнение различных систем обучения очевидно, что в одних системах обучения как бы надстраивается на развитием ( по словам Выготского «плетется в хвосте развития» , оказывая на него стихийное влияние) ,а в других – целенаправленно обеспечивает его, «ведет за собой развитие» и активно использует его для усвоения новых понятий, знаний, умений. В первом случае имеется приоритет информационной функции обучения, его нацеленность на «отработку» знаний, умений, навыков, во втором – приоритет развивающей функции обучения, и это кардинально меняет построений курса обучения. В 70-н годы альтернативными назывались системы, в которых был принят другой порядок изучения математических понятий: В системе Давыдова: величина → отношение → число. В учебниках Виленкина, Петерсон:

величина→

отношение →число

множество→

Сегодня альтернативным называют любой учебник по отношению к традиционному. Многолетний опыт апробации альтернативных учебников показал, что для получения развивающего эффекта недостаточно просто использовать в работе учителя новый учебник. Необходимо владеть методикой математического развития ребенка, чтобы реализовать развивающую функцию математического содержание учебника.

5). Изучение математики в начальных классах строится по концентрам: «десяток», «сотня», «тысяча», «многозначное число». В каждом последующем концентре расширяются и углубляются знания учащихся теме. Такое построение курса позволяет неоднократно возвращаться к его основным вопросам, совершенствую тем самым умения и навыки. преемственность в изучении материала в каждом концентре увеличивает долю самостоятельности учащихся при освоении нумерации в каждом концентре. Основные понятия темы: число, цифра, класс, разряд. Термин число и цифра вводится в концентре «Десяток». В самом начале учитель должен следить за тем чтобы учащиеся не путали понятия число и цифра. Цифра используется для записи чисел. Н-р, для того чтобы записать число 45 мы используем 2 цифры – 4 и 5.

Целые неотрицательные числа называют натуральными в связи с тем что они были придуманы человеком для счетов элементов реальных множеств(животных ,людей, предметов), а т.ж.для обозначения результатов процесса измерения величин (длины, массы, времени и др). Таким образом различают число как результат счета элементов множества и число как результат измерения величин (длина ,масса, время). Альтернативные программы различаются главным образом способом знакомства ребенка с этими характеристика числа. В основе первой трактовки лежит счет предметов, который служит для определения их количества. Число в этом случае выступает как результат счета и характеризует количество предметов данного множества. Число называют количественным. Каждое называемое в процессе счета число ставится в соответствии одному из перечисленных предметов, характеризуя его порядок при счете. Например, всего 3 круга, а закрась второй (это порядковое число). В основе второй трактовки у детей формируется представление о том, что в результате измерения любой величины получается число.

Нуль не считается натуральным числом. При знакомстве с 0 нельзя ссылаться на счет предметов, невозможно выстроить предметную модель нуля. В математике 0 определяют как символ пустого множества. 0 число особое, его можно получить только путем отщипывания. Если из числа вычесть само число то получится 0. Или отщипывать по 1. Число 0 обозначает отсутствии предметов, подлежащих счету. следует правильно формулировать пояснения: Ни осталось ни одной фигуры, которые мы считали. для того чтобы это обозначить, используется специальный знак – цифру 0 (нуль, ноль). При этом не стоит говорить «Ничего нет, значит нуль». Нет яблок в корзине, но корзина, то есть! Нужно так: «Для обозначения того что в корзине яблок больше нет, используют цифру 0. НЕ РЕКОМЕНДУЕТСЯ выстраивать последовательность 0 1 2 3 4 5 в фиксированном виде т.к. ребенок запоминает этот ряд и в дальнейшем становится убежден в том что 0 первое число в натуральном ряду т.е. 0 – натуральное число. при изучении нумерации дети должны осознать свойства натурального ряда чисел: каждое след. число больше предыдущего на 1 и наоборот; наименьшее число 1; ряд бесконечен и дискретен.

Методика изучения числе первого десятка. задачи темы:

- продолжить работу, начатую в подготовительный период;

- познакомить учащихся с математической символикой, знаками «больше, меньше, плюс, минус», показать возможность их использования.

- разъяснить принцип образования натурального ряда чисел.

- вести целенаправленную работу над составом числа. В соответствии с этими задачами строится изучение темы. Последовательное увеличение изучаемых отрезков натурального ряда чисел позволяет учащимся осознать принцип его образования. Следует обратить их внимание на то ,что каждый раз рассматривается весь ранее изученный отрезок натурального ряда и каждое новое число выступает ка его продолжение. Поучение каждого следующего числа в натуральном ряду сначала разъясняется на наглядном материале, а затем записывается с помощью знаков «плюс, минус». Тем саамы осуществляется подготовительная работа к изучению сложения и вычитания. Изучение числа и цифры «1» строится на сопоставлении понятий «один» и «много».

Большая часть нагрузки при освоении счета приходится на механическую память т.е. процесс обучения счету в большей мере репродуктивен. Для того чтобы ребенок не осваивал его на формальном уровне, на первых порах этот процесс следует обязательно сопровождать предметными действиями: откладыванием, показыванием, проговариванием вслух. Следует помнить что можно просить ребенка считать двойками, тройками ,но нельзя говорить: « посчитай от 10 обратно». Процесс счета «векторный» т.е. возможен по определению только в сторону увеличения номеров. Умение называть числительные в обратном порядке является базовым при для обучения ребенка процессу отсчитывания, поэтому формировать такое умение необходимо ,но формулировать его нужно правильно «Назови числа в обратном порядке». так же формулируется задание типа «назови числа от 6 до 9».

6). Данный период совпадает с адаптационным периодом ребенка в школе, следовательно возникают трудности в организации подготовительного периода: 1) низкая концентрация внимания, его рассеянность. 2). быстрая утомляемость. 3). разный уровень подготовленности учащихся. 4). не сформированность элементов учебной деятельности. 5). плохо развитая мелкая моторика рук. В этот период:

- уточняются представления учащихся о количественном и порядковом числе;

- выясняется знание порядка слов-числительных в натуральном ряду чисел и умение последовательно называть их в прямом и обратном порядке ,начиная с любого;

- формируется умение считать предметы. В процессе различных упражнений учащиеся должны усвоить, что:

а). начинать считать можно с любого предмета.

б). в процессе счета следует каждому предмету ставить в соответствие слово-числительное т.е. при счете нельзя не пропустить ни одного предмета, ни поставить в соответствии двум предметам одно слово-числительное.

в). слово-числительное, названное при счете последним, является ответом на вопрос «Сколько?», т.е. характеризует количество предметов данной совокупности.

с помощью установления (наличия или отсутствия) взаимно однозначного соответствия между предметами сравниваемых совокупностей разъясняются понятия «больше», «меньше», 2столько же». Формирование идет полностью на наглядной основе и практическими действиями с предметами. Дети должны уяснить, что больше – это столько же да еще. Н-р, на доске 3 белки. Задание: положи столько кружков сколько белок. Положи столько кружков, чтобы их стало больше (меньше) чем белок. Как получили больше (меньше)? и так 3 аналогичных задания.

7). Задачи изучения темы:

1. Познакомить учащихся с новой счетной единицей – десятком.

2. Ввести понятие «Разряд». Разъяснить что двузначные числа имеют два разряда – единицы и десятки, при этом 10 единиц составляют 1 десяток (особенности построения десятичной системы счисления).

3. Научить читать и записывать двузначные числа.

4. добиться сознательного различения понятий цифры и числа ( в числе 37 две цифры, но они выражают одно двузначное число). Довести до сознания учащихся тот факт, что значение цифры в записи числа зависит от места, на котором она стоит (поместное значение цифр).

5. сформировать умение складывать и вычитать числа на основе знания разрядового состава числа.

6. В тесной связи с изучением нумерации двузначных чисел рассмотреть новые единицы измерения длины (дециметр, метр).

Изучение темы осуществляется в 2 этапа: сначала изучаются числа от 11 до 20, а затем от 20 до 100. Это связано с особенностями образования числительных второго десятка, усвоение которых вызывает у детей трудности. Необходимо разъяснить учащимся закономерность образования названий двузначных чисел от 11 до 20. С этой целью, отсчитав (по одной) десять палочек, учитель связывает их в пучок и вводит новое название «Десяток» (или сокращенной «дцать»). Учащиеся уже знают, что число 10 записывается с помощью двух цифр. Если добавить к десятку 1 палочку т.е. к числу «дцать» число «один», то получится число, которое называется один-на-дцать. После добавления еще одной палочки получают две палочки на «дцать», отсюда название нового числа две –на – дцать. После рассмотрения двух-трех чисел учащиеся сами по аналогии называют соответствующие числительные. Усвоив устную нумерацию в пределах от 11 до 20, учащиеся овладевают записью чисел, выделяя в них единицы и десятки. Большую роль при этом играет наглядность обучения. Термин «Разряд» (единицы 1 и 2 разрядов) вводится при изучении чисел от 21 до 100. В процессе усвоения разрядного состава двузначного числа используется таблица разрядов, абак, выполняются разного рода упражнения.(Как изменится число если его увеличить на 1 десяток; какие сумы являются суммой разрядов слагаемых ; запиши число в виде суммы разрядов слагаемых и др.). Устная и письменная нумерация изучается на 1 уроке. Гл. наглядное средство – таблица разрядов.

8). К изучению этой темы приступают во 2 классе. здесь впервые вводится и разъясняется термин «нумерация». Особенности десятичной системы счисления позволяют осуществить перенос умения читать и записывать двузначные числа на область трехзначных.

Задачи изучения темы:

-познакомить учащихся с новой счетной единицей – сотней и разрядом сотен.

- закрепить усвоение позиционного построения десятичной системы счисления (поместного значения цифр). На примере след. упражнений: что обозначает каждая цифра в записи чисел: 894, 809,408).

- разъяснить соотношение разрядных единиц в трехзначном числе: 10единиц= 1 десяток, 10 десятков=1 сотня.

-научить определять количество десятков и сотен в трехзначном числе (десятичный состав числа).

- сформировать умение ,а затем и навык чтения и записи трехзначного числа.

- сформировать умении складывать и вычитать числа на основе разрядного состава трехзначного числа.

- в связи с изучением трехзначных чисел рассмотреть соотношение единиц длины6 дециметр, метр, километр.

Основные виды заданий, при изучении чисел концентра «тысяча».

1).на способ образования трехзначных чисел: назови число в котором 3сот. 1дес. 9 ед.; сколько всего палочек если есть 2 пучка по 100 палочек, 4 пучка по 10 палочек и 5 палочек.

2). на соотнесения названия и записи числа: прочитай числа записанные в таблице, запиши в таблицу и прочитай числа 7 сот. 3 дес. 3 ед.; назови и запиши числа отложенные на счетах.

3). на принцип образования натурального ряда чисел: какое число при счете следует за числом 199; увеличь на 1: 199, 444, 545.

4). на поместное значение цифры в записи числа (см. выше).

5). на место числа в ряду чисел. (во Дворце спорта в одном ряду были свободны места с 231 по 240. Назови какие места свободны.

6). на разрядный состав: замени число суммой: 345, 943, 567.

7). на сравнение чисел: какое число больше 456 или 374? (сравнивать числа начинаю со старших разрядов).

Завершается изучение концентра «Тысяча» знакомством с числом 1000. 10 сотен=1000. Число 1000 завершает изучение трехзначных чисел. 1000 первое четырехзначное число в ряду натуральных чисел. Тысяча наименьшее четырехзначное число. Тысяча новая счетная единица в десятичной системе счисления.

9). В концентре «Многозначное число» продолжается изучение нумерации. При рассмотрении этой темы особое внимание следует уделить введению и разъяснению понятия «Класс», т.к. от степени понимания учащимися этого материала зависит успешное усвоение ими устной и письменной нумерации многозначных чисел. прежде чем приступать к изучению данной темы необходимо повторить вопросы, которые являются подводящими к данной теме и в которых у учащихся есть пробелы. При ознакомлении учащихся с понятием «класс» широко используется метод объяснения, сочетающийся с применением таких средств наглядности, как счеты, таблица разрядов и классов. следует иметь в виду, что у многих учащихся вызывает затруднения запись чисел, в которых отсутствуют единицы того или иного разряда и использование таблицы разрядов и классов, особенно на этапе закрепления, позволяет уменьшить количество допускаемых ошибок. Кроме того, полезно обращать внимание учащихся на место высшего разряда в числе, т.е. заранее определять количество цифр. например, с помощью таких вопросов:

1). сколько цифр в числе, содержащем 851 тысячу? 3 тысячи и т.д.

учителю стоит постоянно обращать внимание учащихся на структуру многозначного числа. Здесь особенно полезно упражнение на сравнительный анализ чисел, записанных одинаковыми цифрами. Например, В чем сходство и в чем различие чисел: 362521 и 362000531; сравни числа 70004 и 70044 вставь вместо точек такие цифры чтобы запись оказалась верной: 1326˃13.. и т.д.

Большое внимание при изучении нумерации многозначного числа уделяется упражнениям, связанным с определением в числах количества десятков, сотен, тысяч, десятков тысяч, сотен тысяч и т.д. При их выполнении целесообразно использовать таблицу разрядов и классов.

Для усвоения материал темы полезно упражнение на преобразование одних единиц величин в другие, так как этот перевод тесно связан с принципом построения десятичной системы счисления, например, 97858 г = ….кг. Так же перевод одних единиц тесно связан с умножением и делением на 10,100,1000 и т.д. при изучении нумерации многозначных чисел важно обратить внимание учащихся на наименование и запись чисел, следующих за 99,999,9999 …. Именно здесь находит практическое применение знание соотношения разрядных единиц в числе: если к 9 прибавить 1, то получится 10, а это уже единица нового разряда и т.д. Особую трудность у школьников вызывает решение примеров типа 1000 – 1, 10000-1 и т.д. Для того, чтобы в этих случаях дети сознательно подходили к получению результата, можно использовать метод наблюдения, который связан с выявлением определенной закономерности: 9+1=10; 10-1=9

99+1=100; 100-1=99

999+1=1000 1000-1=999

Прибавляя 1 к наибольшему однозначному числу, получаем наименьшее двузначное, прибавляя ее к наибольшему двузначному числу, получаем наименьшее трехзначное и т.д.(Аналогично обобщаются и обратные примеры – второй столбик). Для разъяснения получаемого результата можно предложить следующие упражнения:

9999+1 = (9900 +99) +1 = (99+1) +9900 = 100 +9900 = 10000.

10). В начальной школе изучают 4 арифметических действия: сложение, вычитание, деление и умножение. Сложение и вычитание называют действиями первой ступени. Логика формирования понятий состоит из 3 этапов. Первый – подготовительный. В основе смысла действий сложение и вычитание лежит теоретико-множественный подход, с точки зрения которого сложению соответствуют такие предметные с совокупностями (множествами, группами предметов) как: Увеличение данной совокупности на несколько предметов; увеличение не данной, а другой совокупности на несколько предметов; составление совокупности из 2 других. В связи с этим, прежде чем знакомить с символикой записи действий и вычислениями результатов действий, ребенок должен научиться моделировать на предметных совокупностях все эти ситуации, понимать (т.е. правильно представлять их) со слов учителя, уметь показывать руками как процесс и результат предметного действия, а затем характеризовать их словесно. Действию вычитания соответствуют 4 вида предметных действий: удаление части совокупности; уменьшение данной совокупности на несколько единиц; уменьшение на несколько единиц совокупности, сравниваемой с данной; разностное сравнение двух множеств. После того как ребенок научится понимать на слух и моделировать все вышеперечисленные виды предметных действий, его можно знакомить со знаками действия. Это второй этап логики формирования понятий, на котором появляются новые формы чтения и вводятся новые понятия. На этом этапе последовательность указаний педагога такова:

-Обозначьте то, о чем говорится в задании кружочками( палочками и т.д.)

- обозначьте указанное число кружочков цифрами;

- поставьте между ними необходимый знак. Получаем, н-р, такую запись 4+3 – это математическое выражение. Число 7 называют – значением выражения. Запись вида: 3+4=7 – называют равенством. Или по другому 3+5 – это сумма, а числа 3 и 5 слагаемые. 8 – значение суммы или выражения.

Выражение вида 8-3 называют разностью. 8- уменьшаемое, а число 3 – вычитаемое, а число 5 – значение разности.

После первичного знакомства с компонентами действий сложения и вычитания педагог активно использует упражнения ,направленные на отработку названий компонентов действий. ( из данных выражений выбери то в котором уменьшаемое 10; составь выражение в котором вычитаемое 5; как называются числа в выражении 5-3 и 6+2; найди разность чисел 6 и 2 и т.д. В этом и заключается 3-й этап формирования понятия.

Во 2 классе дети знакомятся с правилами проверки результатов действий сложение и вычитание: сложение можно проверить вычитанием,(из сумы вычли одно слагаемое, получили второе слагаемое, значит сложение выполнено верно), а вычитание сложением (к разности прибавили вычитаемое, получили уменьшаемое, значит вычитание выполнено верно).

11). Свойство перестановки слагаемых (переместительное свойство) используется в 1 классе при знакомстве с вычислительными приемами вида а+5,6,7,8,9. В этих случаях второе слагаемое больше первого. Применение данного свойства позволяет свести все случаи вычисления к ранее изученным. Например, 2+8 =8+2=10. Перестановка слагаемых может рассматриваться как прием вычислений. Этот вычислительный прием облегчает вычислительную деятельность и является общим приемом вычисления при сложении любых чисел. Если случаи вида а+1,2,3,4 изучались совместно со случаями а-1,2,3,4 то случаи для переместительного свойства изучаются по отдельности, сначала на сложение, а после на вычитание( данные случаи связаны с правилом взаимосвязи компонентов и результатов действия). И рассуждение строится по другому: 8-5=(5+3)-5=3. Такое разделение необходимо для того, чтобы не перегружать память ребенка, т.к. случаи таблиц сложения и вычитания могут путать ребенка при решении. Свойство показывают на полной наглядности, 3-хкратный повтор, показывается где свойство применяется, дается общая формула. показать можно следующим образом: дается 3 красных и 2 синих шарика. Это записывается с помощью математических знаков. После красные и синие шарики меняю местами и т.ж.просят записать это с помощью математических знаков. После задаются вопросы что общего? Что заметили? И дается формулировка переместительного свойства сложения. ВАЖНО донести до учащихся, что при использовании переместительного свойства выражение второй раз считать не надо!

1 2 и 13). будешь импровизировать=).

переместительное свойство: а+а=а+а

сочетательное свойство: (а+б)+с=а+(б+с) свойства сложения

свойство нуля: а+0=а

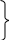
вычитание суммы из числа: а – (б+с) = а-в-с

вычитание числа из суммы: (а+б) – с = а + (б-с) или (а-с) + б свойства вычитания

свойство нуля: а-0=а

14). Схематическое изображение:

В 3 классе дели знакомятся с правилами взаимосвязи компонентов сложения и вычитания , которые являются обобщением представления ребенка о способах проверки сложения и вычитания:

Если из суммы вычесть одно слагаемое, то получится другое слагаемое.

Если сложить разность и вычитаемое, то получится уменьшаемое.

Если из уменьшаемого вычесть разность, то получится вычитаемое.

Данные правила являются основой для подготовки к решению уравнений, которые в начальной школе решаются с опорой на правило нахождения соответствующего неизвестного компонента равенства.

Например: 24 – х = 19. В уравнении неизвестно вычитаемое. Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность:

х = 24 – 19, х=5

15).

16). 1). Организация учебного процесса. В основе объяснительно-иллюстративный метод.

тема и цель → актуализация знаний → объяснение нового материала →закрепление →повторение →контроль.

В основе деятельностный подход.

постановка учебной задачи → открытие нового знания →первичное закрепление →с\р с проверкой в классе →решение задач на повторение →рефлексия (самоконтроль).

17). В системе Л.В. Занкова для 4-летней системы обучения используются учебники Аргинской И.И. Дополнительно к этим учебникам имеются тетради на печатной основе авторов Е.П.Бененсон и Л.С.Итиной.

В системе В.В.Давыдова существует несколько вариантов учебников математики для начальных классов различных авторских коллективов: учебники А.М.Захаравой, Т.И.Фещенко; учебники В.В.Давыдова, С.Ф,Горбова, Г.Г.Микулиной, О.В,Савельевой. Наиболее распространен на сегодняшняя учебник Э.И.Александровой, он включен в Федеральный перечень учебников для начальной школы.

В системе «Гармония» авторами учебников по математике являютс И.Б.Истомина, И.Б.Нефедова.

В системе «Школа 2100» автором является Л.Г.Петерсон. УМК представляет собой 12 тетрадей вида учебник-тетрадь, которые могут быть распределены на все года обучения.

В системе «Начальная школа 21 века» авторами учебников являются Н.В.Рудницкая, Т.В.Юдачева.

Сопоставительный анализ всех 5-ти программ с традиционной показали, что объем изучения нумерации и арифметических действий в них единый. Разница только в распределении тем по годам обучения. Программы Занкова и «Гармония» не рассматривают задачу в 1 классе, но итоговый уровень сложности рассматриваемых в них задач ( в 4 классе) одинаков. Все альтернативные программы содержат значительно больший объем геометрического материала, чем традиционный учебник, при этом значимым отличием является работа с объемными телами и инструментами для построения фигур на плоскости (циркуль, угольник, транспортир).

Программы Аргинской и Александровой содержат значительный по объему материала работы с дробями: первая – с обыкновенными, вторая – с десятичными, в том числе с процентами.

Программы Петерсон и Рудницкой отличаются наибольшим уровнем насыщенности курса математики начальной школы алгебраическим материалом и дробями (в том числе и процентами). Программа Петерсон также знакомит учеников начальных классов с элементами теории множеств, а программа Рудницкой – с элементами формальной логики.

Очевидно, что для работы по упомянутым программам учитель должен обладать достаточно глубокими знаниями математики, а так же быть знакомым с тем, как нетрадиционное для начальной школы содержание( сложные уравнения, дроби, проценты, элементы теории множеств и логики и др.) рассматриваются в МОМ в средней школе, чтобы учитывать требования преемственности обучения.

Каков же главный инструмент реализации развивающей функции обучения математике. В системе Занкова во гласу угла ставится необходимость соблюдать дидактические принципы организации развивающего обучения и опора на систему проблемных ситуаций на уроке. В программе Петерсон, Рудницкой, Александровой основной «вес» развивающего потенциала связан с усложнением арифметической (системы счисления и дроби), алгебраической (уравнения) и формально-логической ( элементы теории множеств и логики) линий содержательного наполнения программ. Это обусловлено значимым влиянием на эти системы взглядов Давыдова на ведущую роль теоретического мышления в развитии ребенка мл. школьного возраста. В программе «Истоминой» основная роль «двигателя развития» ребенка в процессе обучения математике отводится построению методической системы целенаправленного формирования приемов умственных действий (сравнения, обобщения, классификации, аналогии и др.). Такой подход позволяет без особых содержательных изменений традиционного объема в обучении математике нацелить обучающий процесс на развитие таких способов познания ребенка , которые становятся достоянием субъекта, характеризуя его интеллектуальный потенциал и познавательные способности.

18). Действие деление рассматривается в начальной школе как действие обратное умножению. С теоретико-множественной точки зрения смыслу деления соответствует операция разбиения множества на равночисленные подмножества. Таким образом, процесс нахождения результатов действия деления связан с предметными действиями двух видов:

а). разбиение множества на равные части (н-р, 8 кружков разложили в 4 коробки поровну, раскладывают по 1, а потом считают по сколько в каждой коробке кружков). («ДЕЛЕНИЕ НА РАВНЫЕ ЧАСТИ»). (частное в данном случае обозначает – количество элементов в каждой части).

б). разбиение множества на части по сколько-то с каждой части( н-р, 8 кружков разложили в коробки по 4 штуки в коробки, а затем считают сколько получилось коробок; деление по этому принципу в методике называется «ДЕЛЕНИЕ ПО СОДЕРЖАНИЮ»). (частное обозначает - число подмножеств на которое разделили данное множество).

Проще для детей деление по содержанию, поэтому знакомство с деление начинают с него. После знакомятся с делением на равные части.

Решая подобного вида задачи дети находят результаты деления и знакомятся с его компонентами. Выражение вида 12:6 называют частным. Число 12 в этой записи называют делимым, 6 – делитель. Запись вида 12:6=2 – называют равенством. Число 2 – значением частного или выражения.

Поскольку названия компонентов действия деления вводятся по соглашению ( детям сообщаются эти названия и их необходимо запомнить), педагог активно использует задания, требующие распознавания компонентов действий и употребления из названий в речи. ( Н-р, Среди данных выражений найди те, в которых делитель равен 3; составь частное, в котором делимое 15. Реши его; выбери примеры, в которых частное равно 6; как называются числа в записи 12:2; делимое 8, делитель 2, частное?

В 3 классе дети знакомятся с правилом взаимосвязи компонентов деления, которое является основой для обучения нахождению неизвестных компонентов деления при решении уравнений:

если делитель умножить на частное, то поучится делимое.

если делимое разделить на частное, то получится делитель.

н-р, решите уравнение 16:х=2. Чтобы найти делитель нужно делимое разделить на частное: 16:2 = 8. х=8.

Однако данные правила в учебнике математики 3 класса не являются обобщением представлений ребенка о способах проверки действия деления. Правило проверки результатов деления рассматривается в учебнике после знакомства с внетабличным умножением и делением (знакомства с умножением и делением двузначных чисел на однозначные, не входящим в таблицу умножения и деления), перед последним самым трудным случаем делении вида 87:29. Это объясняется тем, что получение результатов деления в этом случае представляет собой сложный процесс подбора частного с постоянной его проверкой умножением, поэтому правило проверки действия деления дети рассматривают даже раньше, чем правило проверки действия умножения. Правило проверки действия деления:

1). Частное умножают на делитель.

2). Сравнивают полученный результат с делимым. Если эти числа равны, деление выполнено верно.

н-р, 78:3= 26. 1) 26*3 = 78. 2)78=78.

19). Изучение таблицы умножения является центральной задачей обучения математике во 2 и 3 классах. К табличному умножению относят случаи умножения однознач. нат. чисел на однознач. нат. числа, результаты которых находят на основе конкретного смысла действия умножения (находят суммы одинаковых слагаемых). Результаты табличного умножения учащееся должны знать наизусть .Случаи умножения с числами 0, 1 и 10 относятся к особым случаям. Первые приемы составления таблиц умножения связаны со смыслом действия умножения. Результаты этих таблиц получают последовательным сложением одинаковых слагаемых. н-р, умножение числа 2.

в ычисли и запомни:

2 +2 2*2

2 +2+2 2*3

2+2+2+2 2*4

Расположенный рядом рисунок помогает ребенку получить результат путем пересчета фигурок. При небольших значениях множителей прием сосчитывания для получения табличного значения произведения вполне приемлен, и учитель им часто пользуется при получении результатов таблиц значений умножения числе 2,3,4. Приведенный пример показывает, что этот прием удобен лишь при небольших значениях второго множителя. При значении второго множителя больше 5, удобнее использовать для получения результатов табличных значений другой прием: прием прибавления к предыдущему результату. н-р, вычисли и запомни:

2*6 = 2*5+2

2*7= 2*6+2

2*8=2*7+2

Данный прием в учебнике 2 класса дан более пространно. Аналогично составляется таблица умножения числа 3.

Следующим приемом, на основе которого составляются таблицы значений умножения чисел, является прием перестановки множителей. Этот прием фактически является первичным математическим законом относительно действия умножения в начальной школе: от перестановки множителей произведение не меняется. Способ знакомства детей с этим правилом обуславливается ранее введенным смыслом действия умножения. Используя предметные модели множеств, дети сосчитывают результаты группировки их элементов разными способами, убеждаясь, что результаты не меняются от изменения способов группировки.(2*3=6 и 3*2=6

Счет элементов рисунка парами по горизонтали совпадает со счетом элементов тройками по вертикали. )

На основе этого правила, используемого как прием счета, составляется таблица умножения на 2. н-р, используя таблицу умножения числа 2, вычисли и запомни таблицу умножения на 2:

2 *3=6 3*2=6

2 *4=8 4*2=8

2 *5=10 5*2=10

2 *6=12 6*2=12

На основе этого же приема составляется таблица на 3. Составление двух первых таблиц распределяется на 2 урока, что соответственно увеличивает время, отведенное на заучивание. Каждая из двух последних таблиц составляется на одном уроке, поскольку предполагается, что дети, зная исходную таблицу, не должны отдельно заучивать результаты таблиц, полученных с помощью перестановки множителей. На самом деле многие учащиеся заучивают каждую таблицу отдельно потому что случаи вида 3*8 и 8*3 рассматриваются через довольно большой промежуток времени и у учащихся не возникает ассоциативной связи между этими случаями. При составлении таблицы умножения числа 5, только первое произведение составляется путем сложения одинаковых слагаемых. Остальные случаи получают приемом прибавления 5 к предыдущему результату:

5*6=5*5+5=30

5*7=5*6+5=35 и т.д. Одновременно с этой таблицей составляется и взаимосвязанная таблица умножения на 5: 6*5; 7*5; 8*5 и т.д.

Большой объем материала, требующего заучивания наизусть, сложность в образовании ассоциативных связей при запоминании взаимосвязанных случаев, необходимость достижения всеми детьми прочного запоминания всех табличных случаев наизусть в установленные программой сроки – это делает тему изучения табличного умножения в начальных классах одной из наиболее методически сложных.

Д еление рассматривается как действие обратное умножению. В связи с этим сначала дети знакомятся со случаями деления без остатка в пределах 100 – так называемым табличным делением. С действием деления дети знакомятся после того как выучили наизусть таблицы умножения чисел 2 и 3. На основе знания этих таблиц уже на 4 уроке после знакомства с делением, составляется первая таблица деления на 2. Для получения ее значении используют предметный рисунок.

2:2 = 4:2= 6:2= 8:2=

Значение частных в этой таблице получают подсчетом элементов рисунка на картинке.

Следующая таблица деления – деление на 3 является последней таблицей, изучаемой во 2 классе. Составляется она на основе взаимосвязи компонентов умножения с использованием правила нахождения неизвестного множителя. Но т.к. данное правило в полном виде дается только в 3 классе, на этапе составления таблицы деления на 3 целесообразно опираться на предметную модель действия. (задание вида: вычисли, запомни результат и проверь по рисунку). Использование рисунка позволяет составлять 3 взаимосвязанных таблицы:

3*3=9 9:3=3

4*3=12 12:3=4 12:4=3 и т.д.

Все остальные таблицы изучаются в 3 классе. Поскольку таблица умножения числа 4 и на 4 изучается в 3 классе, на втором году обучения прекращается практика раздельного изучения таблиц умножения и деления. Начиная с таблицы умножения числа 4, взаимосвязанные с ней таблицы деления изучаются на 1 уроке.

4*4=16 16:4

4*5=20 5*4 20:4 20:5

Используя результаты первого столбика, дети получают второй столбик перестановкой множителей, а результаты третьего и четвертого столбиков – на основе правила взаимосвязи компонентов умножения:

Если произведении разделить на один из множителей, то получится другой множитель.

Все остальные таблицы деления получаются аналогичным способом.

20). К Внетабличным случаям умножения и деления в пределах 100 относятся случаи умножения двузначного числа на однозначное (20*3, 18*3), а т.ж. случаи деления двузначного числа на однозначное, не водящие в число табличных ( 80:4, 96:6) и случаи деления двузначного на двузначное в пределах 100 (80:40, 96:16). Эти случаи рассматриваются как случаи устных вычислений, и предполагается, что ребенок выполняет их без обращения к письменным алгоритмам вычислений, а лишь использует известные ему правила и законы арифметических действий и знание табличного умножения и деления.