
- •1.3. Энергия электромагнитных волн
- •Импульс электромагнитного поля
- •7.8. Эффективные значения тока и напряжения
- •Цепи переменного тока
- •2.14. Резонанс токов
- •Цепи переменного тока
- •Резонанс напряжений
- •Свободные незатухающие колебания в lc-контуре
- •Переменный ток
- •Свободные незатухающие колебания в lc-контуре
- •Энергия магнитного поля.
- •Взаимная индуктивность контуров
- •Векторная форма
- •Потенциальная форма
- •Условия на границе раздела двух магнетиков
- •Природа ферромагнетизма
- •Диамагнетизм и парамагнетизм
- •2. Заряженная частица движется перпендикулярно линиям магнитной индукции
- •3. Скорость заряженной частицы направлена под углом к вектору.
- •Контур с током в магнитном поле
- •Вращающий момент (или момент силы)
Энергия магнитного поля.
Проводник, по которому протекает электрический ток, создает в окружающем пространстве магнитное поле, причем магнитное поле появляется и исчезает вместе с появлением и исчезновением тока.
Магнитное
поле, подобно электрическому, является
носителем энергии. Естественно
предположить, что энергия магнитного
поля равна работе, которая затрачивается
током на создание этого поля.
Рассмотрим
контур индуктивностью L, по которому
течет ток I. С данным контуром сцеплен
магнитный поток [см. (126.1)] Ф = LI, причем
при изменении тока на dS магнитный поток
изменяется на dФ = Ldl. Однако для изменения
магнитного потока на величину dФ
необходимо совершить работу dA = IdФ —
LIdI. Тогда работа по созданию магнитного
потока будет
![]() Следовательно,
энергия магнитного поля, связанного с
контуром,
Следовательно,
энергия магнитного поля, связанного с
контуром,
![]() (130.1)
Исследование
свойств переменных магнитных полей, в
частности распространения электромагнитных
волн, явилось доказательством того, что
энергия магнитного поля локализована
в пространстве. Это соответствует
представлениям теории поля.
Энергию
магнитного поля можно представить как
функцию величин, характеризующих это
поле в окружающем пространстве. Для
этого рассмотрим частный случаи —
однородное магнитное поле внутри
длинного соленоида. Подставив в формулу
(130.1) выражение (126.2), получим
(130.1)
Исследование
свойств переменных магнитных полей, в
частности распространения электромагнитных
волн, явилось доказательством того, что
энергия магнитного поля локализована
в пространстве. Это соответствует
представлениям теории поля.
Энергию
магнитного поля можно представить как
функцию величин, характеризующих это
поле в окружающем пространстве. Для
этого рассмотрим частный случаи —
однородное магнитное поле внутри
длинного соленоида. Подставив в формулу
(130.1) выражение (126.2), получим
![]() Поскольку
Поскольку ![]() и
и ![]() ,
то
,
то ![]() (130.2)
где
(130.2)
где ![]() -
объем соленоида.
Магнитное
поле соленоида однородно и сосредоточено
внутри пего, поэтому энергия [см. (130.2)]
заключена в объеме соленоида и распределена
в нем с постоянной объемной
плотностью
-
объем соленоида.
Магнитное
поле соленоида однородно и сосредоточено
внутри пего, поэтому энергия [см. (130.2)]
заключена в объеме соленоида и распределена
в нем с постоянной объемной
плотностью
![]() Формула
(130.3) выведена для однородного поля, но
она справедлива и для неоднородных
полей. Выражение (130.3) справедливо только
для сред, для которых зависимость B от
H линейная, т.е. оно относится только к
пара- и диамагнетикам
Формула
(130.3) выведена для однородного поля, но
она справедлива и для неоднородных
полей. Выражение (130.3) справедливо только
для сред, для которых зависимость B от
H линейная, т.е. оно относится только к
пара- и диамагнетикам
Билет 31
Возьмем два контура, расположенные недалеко друг от друга, как это показано на рисунке 5.4.
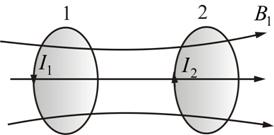 Рис.
5.4
Рис.
5.4
В
первом контуре течет ток ![]() .
Он создает магнитный поток, который
пронизывает и витки второго контура.
.
Он создает магнитный поток, который
пронизывает и витки второго контура.
![]() ,
(5.3.1)
,
(5.3.1)
При изменении тока во втором контуре наводится ЭДС индукции:
![]() ,
(5.3.2)
,
(5.3.2)
Аналогично,
ток ![]() второго
контура создает магнитный поток,
пронизывающий первый контур:
второго
контура создает магнитный поток,
пронизывающий первый контур:
![]() ,
(5.3.3)
,
(5.3.3)
И при изменении тока наводится ЭДС:
![]() ,
(5.3.4)
,
(5.3.4)
Контуры
называются связанными,
а явление – взаимной
индукцией.
Коэффициенты ![]() и
и ![]() называются взаимной
индуктивностью,
или коэффициентами
взаимной индукции.
Причём
называются взаимной
индуктивностью,
или коэффициентами
взаимной индукции.
Причём ![]()
Трансформатор является типичным примером двух связанных контуров. Рассмотрим индуктивность трансформатора и найдем коэффициент трансформации.
Взаимная индуктивность контуров
Если имеется два независимых контура тока, то между ними существует взаимная индуктивность. Взаимная индуктивность есть число линий магнитного потока, вызванных током в один ампер в одном контуре, которые охватывают провод с током второго контура.
При изменении тока в одном контуре создаваемое напряжение в другом контуре составляет
Vn = M(dI/dt), (2.61)
где Vn — индуцированное напряжение в одном контуре; M — взаимная индуктивность между двумя контурами; dI/dt — скорость изменения тока в другом контуре.
Напряжение помех возникает только в том случае, когда происходит изменение тока. Помехи этого типа называются помехами переключения, или синхронными коммутационными помехами. В ряде источников встречается термин «помехи типа дельта I».
Наиболее важно для снижения уровня коммутационных помех уменьшать взаимную индуктивность между контурами. Это может быть достигнуто разнесением контуров. Взаимная индуктивность между контурами не может быть больше, чем собственная индуктивность меньшего контура. Поэтому для снижения взаимной индуктивности необходимо снижать собственную индуктивность контуров.
Взаимная индуктивность определяет уровень перекрестных помех между сигнальными проводниками.
Коэффициент трансформации
Действие трансформатора основано на явлении электромагнитной индукции. При прохождении переменного тока по первичной обмотке в сердечнике появляется переменный магнитный поток, который возбуждает ЭДС индукции в каждой обмотке. Сердечник из трансформаторной стали концентрирует магнитное поле, так что магнитный поток существует практически только внутри сердечника и одинаков во всех его сечениях. Мгновенное значение ЭДС индукции в любом витке первичной или вторичной обмотки одинаково. Согласно закону Фарадея оно определяется формулой: е = -Ф’ где Ф' - производная потока магнитной индукции по времени, еcли Ф = Фт cos wt, то Ф' = -wФm sin wt. Следовательно е = wФт sin wt, или е = Eт sin wt, где Em = wФm - амплитуда ЭДС в одном витке. В первичной обмотке, имеющей N1 витков, полная ЭДС индукции е1 равна N1e. Во вторичной обмотке полная ЭДС индукции е2 равна N2e (N2 - число витков этой обмотки). Отсюда следует, что N1/N2 = e1/е2 Обычно активное сопротивление обмоток трансформатора мало, и им можно пренебречь. В этом случае модуль напряжения на зажимах катушки приблизительно равен модулю ЭДС индукции: |u1| ≈ |e1| (1) При разомкнутой вторичной обмотке трансформатора ток в ней не течет и имеет место соотношение: |u2| ≈ |e2| (2) Мгновенные значения ЭДС е1 и е2 изменяются синфазно (одновременно достигают максимума и одновременно проходят через нуль). Поэтому их отношение в формуле можно заменить отношением действующих значений E1 и E2 этих ЭДС или, учитывая равенства (1) и (2), отношением действующих значений напряжений U1 и U2: U1/U2 ≈ E1/E2 = N1/N2 = К Величина К - коэффициент трансформации. При К>1 трансформатор является понижающим, а при К<1 — повышающим трансформатором.
Билет 30
Явление самоиндукции
До сих пор мы рассматривали изменяющиеся магнитные поля, не обращая внимание на то, что является их источником. На практике чаще всего магнитные поля создаются с помощью различного рода соленоидов, т.е. многовитковых контуров с током.
Здесь возможны два случая: при изменении тока в контуре изменяется магнитный поток, пронизывающий: а) этот же контур; б) соседний контур.
ЭДС индукции, возникающая в самом же контуре, называется ЭДС самоиндукции, а само явление – самоиндукция.
Если же ЭДС индукции возникает в соседнем контуре, то говорят о явлении взаимной индукции.
Ясно, что природа явления одна и та же, а разные названия использованы для того, чтобы подчеркнуть место возникновения ЭДС индукции.
Явление самоиндукции открыл американский ученый Дж. Генри.
Явление самоиндукции можно определить следующим образом.
Ток I, текущий в любом контуре, создает магнитный поток Ф, пронизывающий этот же контур. При изменении I будет изменяться Ф. Следовательно, в контуре будет наводиться ЭДС индукции.
Т.к.
магнитная индукция В пропорциональна
току I ![]() следовательно
следовательно
![]() где L –
коэффициент пропорциональности,
названный индуктивностью
контура.
где L –
коэффициент пропорциональности,
названный индуктивностью
контура.
Если
внутри контура нет ферромагнетиков,
то ![]() (т.к.
(т.к. ![]() ).
).
Индуктивность контура L зависит от геометрии контура, числа витков, площади витка контура.
За
единицу индуктивности в СИ принимается
индуктивность такого контура, у которого
при токе ![]() возникает
полный поток
возникает
полный поток ![]() .
Эта единица называется Генри (Гн).
.
Эта единица называется Генри (Гн).
Размерность индуктивности:
![]()
Вычислим
индуктивность соленоида L.
Если длина соленоида l гораздо
больше его диаметра d ( ![]() ), то
к нему можно применить формулы для
бесконечно длинного соленоида. Тогда
), то
к нему можно применить формулы для
бесконечно длинного соленоида. Тогда
![]()
здесь N –
число витков. Поток через каждый из
витков ![]()
Потокосцепление
![]()
![]() Но
мы знаем, что
Но
мы знаем, что ![]() ,
откуда индуктивность соленоида
,
откуда индуктивность соленоида
![]()
где n –
число витков на единицу длины, т.е. ![]() –
объем соленоида, значит
–
объем соленоида, значит
![]() (5.1.1)
(5.1.1)
Из этой формулы можно найти размерность для магнитной постоянной:
![]()
При изменении тока в контуре возникает ЭДС самоиндукции, равная:
![]()
![]() (5.1.2)
(5.1.2)
Знак минус в этой формуле обусловлен правилом Ленца.
Явление самоиндукции играет важную роль в электротехнике и радиотехнике. Как мы увидим дальше, благодаря самоиндукции происходит перезарядка конденсатора, соединенного последовательно с катушкой индуктивности, в результате в такой LC-цепочке (колебательном контуре) возникают электромагнитные колебания.
Между
величиной тока в проводнике и величиной
магнитного поля (магнитного потока Ф)
существует прямая зависимость:
-![]() индуктивность проводника L - коэффициент
пропорциональности между Ф и
I.
Индуктивность L зависит от
свойств самого проводника
(его формы, размеров, количества
витков и
т.п., а также магнитной
проницаемости среды μ).
Так магнитное поле катушки (соленоида)
много сильнее магнитного поля прямого
проводника при прочих равных условиях.
L
не зависит от силы
тока I, магнитного
поля Ф и
т.п.
Формулы, где встречается
L:
индуктивность проводника L - коэффициент
пропорциональности между Ф и
I.
Индуктивность L зависит от
свойств самого проводника
(его формы, размеров, количества
витков и
т.п., а также магнитной
проницаемости среды μ).
Так магнитное поле катушки (соленоида)
много сильнее магнитного поля прямого
проводника при прочих равных условиях.
L
не зависит от силы
тока I, магнитного
поля Ф и
т.п.
Формулы, где встречается
L:
![]() -
ЭДС самоиндукции при изменении тока в
проводнике.
-
ЭДС самоиндукции при изменении тока в
проводнике.
![]() -
энергия магнитного поля катушки с током.
-
энергия магнитного поля катушки с током.
-![]() формула Томсона для периода электромагнитных
колебаний в колебательном контуре LC.
формула Томсона для периода электромагнитных
колебаний в колебательном контуре LC.
Токи при размыкании и замыкании цепи
При всяком изменении силы тока в проводящем контуре возникает э. д. с. самоиндукции, в результате чего в контуре появляются дополнительные токи, называемые экстратоками самоиндукции. Экстратоки самоиндукции, согласно правилу Ленца, всегда направлены так, чтобы препятствовать изменениям тока в цепи, т. е. направлены противоположно току, создаваемому источником. При выключении источника тока экстратоки имеют такое же направление, что и ослабевающий ток. Следовательно, наличие индуктивности в цепи приводит к замедлению исчезновения или установления тока в цепи.
![]()
Рассмотрим
процесс выключения тока в цепи, содержащей
источник тока с э.д.с. ![]() ,
резистор сопротивлением R и катушку
индуктивностью L. Под действием внешней
э. д. с. в цепи течет постоянный ток
,
резистор сопротивлением R и катушку
индуктивностью L. Под действием внешней
э. д. с. в цепи течет постоянный ток
![]()
(внутренним
сопротивлением источника тока
пренебрегаем). Разложение
Фурье Любое
сложное периодическое колебание >![]() можно
представить в виде суммы простых
гармонических колебаний с циклическими
частотами, кратными основной циклической
частоте
можно
представить в виде суммы простых
гармонических колебаний с циклическими
частотами, кратными основной циклической
частоте ![]() :
:
В
момент времени t=0 отключим источник
тока. Ток в катушке индуктивностью L
начнет уменьшаться, что приведет к
возникновению э.д.с. самоиндукции ![]() препятствующей,
согласно правилу Ленца, уменьшению
тока. В каждый момент времени ток в цепи
определяется законом Ома I=
препятствующей,
согласно правилу Ленца, уменьшению
тока. В каждый момент времени ток в цепи
определяется законом Ома I=![]() s/R,
или
s/R,
или
![]() (127.1)
(127.1)
Разделив
в выражении (127.1) переменные,
получим ![]() Интегрируя
это уравнение по I (от I0 до I) и t (от 0 до
t), находим ln (I /I0) = –Rt/L, или
Интегрируя
это уравнение по I (от I0 до I) и t (от 0 до
t), находим ln (I /I0) = –Rt/L, или
![]() (127.2)
(127.2)
где t=L/R — постоянная, называемая временем релаксации. Из (127.2) следует, что t есть время, в течение которого сила тока уменьшается в е раз.
Таким образом, в процессе отключения источника тока сила тока убывает по экспоненциальному закону (127.2) и определяется кривой 1 на рис. 183. Чем больше индуктивность цепи и меньше ее сопротивление, тем больше t и, следовательно, тем медленнее уменьшается ток в цепи при ее размыкании.
При
замыкании цепи помимо внешней э. д.
с.
возникает
э. д. с. самоиндукции ![]() препятствующая,
согласно правилу Ленца, возрастанию
тока. По закону Ома,
препятствующая,
согласно правилу Ленца, возрастанию
тока. По закону Ома, ![]() или
или
![]()
Введя
новую переменную ![]() преобразуем
это уравнение к виду
преобразуем
это уравнение к виду
![]()
где t — время релаксации.

В момент замыкания (t=0) сила тока I = 0 и u = – . Следовательно, интегрируя по и (от – до IR– ) и t (от 0 до t), находим ln[(IR– )]/– = —t/t, или
![]() (127.3)
(127.3)
где ![]() —
установившийся ток (при t®¥).
—
установившийся ток (при t®¥).
Таким
образом, в процессе включения источника
тока нарастание силы тока в цепи задается
функцией (127.3) и определяется кривой 2
на рис. 183. Сила тока возрастает от
начального значения I=0 и асимптотически
стремится к установившемуся значению![]() .
Скорость нарастания тока определяется
тем же временем релаксации t=L/R, что
и убывание тока. Установление тока
происходит тем быстрее, чем меньше
индуктивность цепи и больше ее
сопротивление.
.
Скорость нарастания тока определяется
тем же временем релаксации t=L/R, что
и убывание тока. Установление тока
происходит тем быстрее, чем меньше
индуктивность цепи и больше ее
сопротивление.
Оценим
значение э.д.с. самоиндукции ![]() ,
возникающей при мгновенном увеличении
сопротивления цепи постоянного тока
от R0 до R. Предположим, что мы размыкаем
контур, когда в нем течет установившийся
ток
.
При размыкании цепи ток изменяется по
формуле (127.2). Подставив в нее выражение
для I0 и t, получим
,
возникающей при мгновенном увеличении
сопротивления цепи постоянного тока
от R0 до R. Предположим, что мы размыкаем
контур, когда в нем течет установившийся
ток
.
При размыкании цепи ток изменяется по
формуле (127.2). Подставив в нее выражение
для I0 и t, получим
![]()
Э.д.с. самоиндукции
![]()
т. е. при значительном увеличении сопротивления цепи (R/R0>>1), обладающей большой индуктивностью, э.д.с. самоиндукции может во много раз превышать э.д.с. источника тока, включенного в цепь. Таким образом, необходимо учитывать, что контур, содержащий индуктивность, нельзя резко размыкать, так как это (возникновение значительных э.д.с. самоиндукции) может привести к пробою изоляции и выводу из строя измерительных приборов. Если в контур сопротивление вводить постепенно, то э.д.с. самоиндукции не достигнет больших значений.
Особенности спектральной плотности амплитуд сигналов с неограниченной энергией. Автокорреляционная и взаимнокорреляционная функции сигналов, их связь с энергетическими и спектральными характеристиками. Практическая ширина спектра сигнала. Распределение энергии в спектре непериодического сигнала. Основные критерии оценки практической ширины спектра сигнала. Примеры корреляционных функций импульсных сигналов.
Билет 29
Электромагнитная индукция — явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через него.
Электромагнитная индукция была открыта Майклом Фарадеем 29 августа[источник не указан 307 дней] 1831 года. Он обнаружил, что электродвижущая сила, возникающая в замкнутом проводящем контуре, пропорциональна скорости изменения магнитного потока через поверхность, ограниченную этим контуром. Величина электродвижущей силы (ЭДС) не зависит от того, что является причиной изменения потока — изменение самого магнитного поля или движение контура (или его части) в магнитном поле. Электрический ток, вызванный этой ЭДС, называется индукционным током.
Закон Фарадея
Согласно закону электромагнитной индукции Фарадея (в СИ):
![]()
где
![]() — электродвижущая
сила,
действующая вдоль произвольно выбранного
контура,
— электродвижущая
сила,
действующая вдоль произвольно выбранного
контура,
![]()
![]() — магнитный
поток через
поверхность, натянутую на этот контур.
— магнитный
поток через
поверхность, натянутую на этот контур.
Знак «минус» в формуле отражает правило Ленца, названное так по имени русского физика Э. Х. Ленца:
Индукционный ток, возникающий в замкнутом проводящем контуре, имеет такое направление, что создаваемое им магнитное поле противодействует тому изменению магнитного потока, которым был вызван данный ток.
Для катушки, находящейся в переменном магнитном поле, закон Фарадея можно записать следующим образом:
![]()
где
— электродвижущая сила,
![]() —
число
витков,
—
число
витков,
— магнитный поток через один виток,
![]() — потокосцепление катушки.
— потокосцепление катушки.
