Свободные незатухающие колебания в lc-контуре

          Рассчитаем силу тока в LC контуре (рис.1), который включает индуктивность  , емкость   и подключен  к ЭДС  , изменяющейся  по гармоническому закону (1) с частотой колебаний   

  .                                  (1)

 

Из закона Ома для полной цепи вытекает второй закон Кирхгофа:

 cумма всех ЭДС в контуре с учетом знака равна  сумме падений напряжений в нем.

Для LC-контура отсюда следует 

,                                    (2)

Подставляя ЭДС самоиндукции   и напряжение на конденсаторе  , имеем дифуравнение

.               (3)                                              

Свободные электромагнитные колебания совершаются при отсутствии в контуре источника ЭДС,  т.е. когда  . Тогда 

  .                        (4)

Здесь   . (В действительности  наличие источника ЭДС всегда необходимо для  выведения системы из состояние равновесия,  т.е. для первоначальной зарядки конденсатора зарядом  . Свободные  колебания возникают в контуре сразу же после отключения ЭДС источника).

Решением  однородного линейного дифференциального уравнения второй степени (4) является  функция

.                                 (5)

Используя эту функцию для нахождения  ,   и  ,   имеем

      ,

  ,                    (6)

.

Здесь    -  амплитуда колебаний заряда на обкладках конденсатора, 

  - амплитуда колебаний напряжения на обкладках конденсатора,

 –  амплитуда колебаний тока в цепи,

      –  амплитуда колебаний ЭДС самоиндукции.

Сопоставляя выражения для напряжения   и тока  , заключаем, что ток в контуре опережает по фазе напряжение на обкладках конденсатора, а также заряд и ЭДС индукции, на π/2. При этом в момент, когда ток достигает максимального значения, напряжение на обкладках конденсатора  обращается в нуль, и наоборот. Графики зависимостей    и    представлены на рисунке 2.   

Сравнивая амплитуды колебаний напряжения и тока, замечаем, что

    

Эту же формулу можно было бы получить, исходя из того, что наибольшее значение энергии электрического поля    должно быть равно наибольшему значению энергии магнитного поля  .

 

Таким образом, в LC контуре наблюдаются незатухающие гармонические колебания с собственной частотой колебаний

.

Выражение для периода собственных колебаний   называется формулой Томсона.

 

RLC-контур. Свободные затухающие колебания.

 

Рассчитаем силу тока в RLC-контуре, подключенном к источнику ЭДС, изменяющейся  по  закону (1), и включающем дополнительно к индуктивности L и емкости C еще и сопротивление R (рис. 3). 

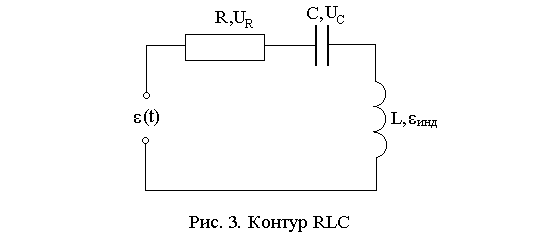
Воспользуемся вторым законом Кирхгофа: сумма всех ЭДС в контуре равна  сумме падений напряжений в нем

,                                        (7)

 где         ,    

  ,                                                 (8)                                                        

.                                                                       

Подставляя (8) в (7),  имеем после деления на   дифуравнение

.                    (9)                                              

Свободные электромагнитные колебания совершаются при отсутствии в контуре источника ЭДС, т.е. при условии  . Тогда 

.                           (10)

Здесь     – коэффициент затухания колебаний. Общее решение однородного линейного  дифференциального уравнения второй степени (10) различно для двух разных случаев.

В  случае    (т.е.   ) имеем решение, описывающее затухающие колебания заряда

,                  (11)

где      – заряд на обкладках конденсатора в начальный момент времени,

 – уменьшающаяся со временем амплитуда колебаний заряда на обкладках конденсатора,

 – частота свободных затухающих  колебаний контура (заметим, что   меньше частоты собственных  незатухающих колебаний  ).

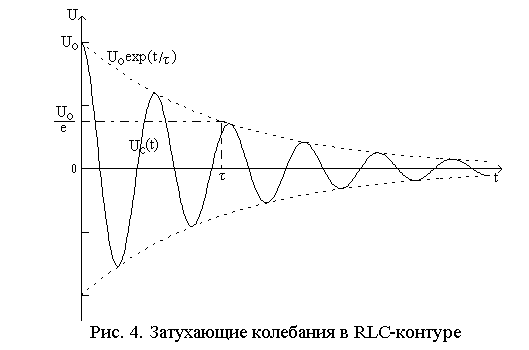
Соответственно для напряжения на обкладках конденсатора имеем представленные графически на рис. 4 затухающие колебания

               .           (12) 

Здесь   - напряжение на обкладках конденсатора в начальный момент    времени,    - уменьшающаяся со временем амплитуда колебаний напряжения на обкладках конденсатора.

 Таким образом, в RLC-контуре наблюдаются свободные затухающие  колебания с частотой

                         (13)

 и коэффициентом затухания         .                (14)

Период затухающих колебаний определяется формулой

  .                          (15)

В случае     (т.е.   или  ) происходит апериодический разряд конденсатора. Колебания при этом не возникают. Омическое сопротивление контура  называется критическим  .

 

Билет 32