Свободные незатухающие колебания в lc-контуре

Рассчитаем силу тока в LC контуре (рис.1), который включает индуктивность  , емкость   и подключен  к ЭДС  , изменяющейся  по гармоническому закону (1) с частотой колебаний   

   .                   

                (1)

Из закона Ома для полной цепи вытекает второй закон Кирхгофа:

 cумма всех ЭДС в контуре с учетом знака равна  сумме падений напряжений в нем.

Для LC-контура отсюда следует 

    ,                                    (2)

Подставляя ЭДС самоиндукции   и напряжение на конденсаторе  , имеем дифуравнение

      .               (3)                                              

Свободные электромагнитные колебания совершаются при отсутствии в контуре источника ЭДС,  т.е. когда  . Тогда 

  .                        (4)

Здесь   . (В действительности  наличие источника ЭДС всегда необходимо для  выведения системы из состояние равновесия,  т.е. для первоначальной зарядки конденсатора зарядом  . Свободные  колебания возникают в контуре сразу же после отключения ЭДС источника).

Решением  однородного линейного дифференциального уравнения второй степени (4) является  функция

.                                 (5)

Используя эту функцию для нахождения  ,   и  ,   имеем

              ,

                ,                    (6)

           .

Здесь    -  амплитуда колебаний заряда на обкладках конденсатора, 

        - амплитуда колебаний напряжения на обкладках конденсатора,

      –  амплитуда колебаний тока в цепи,

      –  амплитуда колебаний ЭДС самоиндукции.

Сопоставляя выражения для напряжения   и тока  , заключаем, что ток в контуре опережает по фазе напряжение на обкладках конденсатора, а также заряд и ЭДС индукции, на π/2. При этом в момент, когда ток достигает максимального значения, напряжение на обкладках конденсатора  обращается в нуль, и наоборот. Графики зависимостей    и    представлены на рисунке 2.  

 

Сравнивая амплитуды колебаний напряжения и тока, замечаем, что

    

Эту же формулу можно было бы получить, исходя из того, что наибольшее значение энергии электрического поля    должно быть равно наибольшему значению энергии магнитного поля  .

 

Таким образом, в LC контуре наблюдаются незатухающие гармонические колебания с собственной частотой колебаний

  .

Выражение для периода собственных колебаний   называется формулой Томсона.

Переменный ток

Большинство потребителей электрической энергии работает на переменном токе. В настоящее время почти вся электрическая энергия вырабатывается в виде энергии переменного тока. Это объясняется преимуществом производства и распределения этой энергии. Переменный ток получают на электростанциях, преобразуя с помощью генераторов механическую энергию в электрическую. Основное преимущество переменного тока по сравнению с постоянным заключается в возможности с помощью трансформаторов повышать или понижать напряжение, с минимальными потерями передавать электрическую энергию на большие расстояния. Кроме того, генераторы и двигатели переменного тока более просты по устройству, надежней в работе и проще в эксплуатации по сравнению с машинами постоянного тока.

Переменным током называется электрический ток, сила которого каким-либо образом меняется со временем. Обычный способ получения переменного тока заключается в том, что при вращении рамки в однородном магнитном поле в ней возникает электродвижущая сила, которая по закону Фарадея равна

.

Если рамка вращается в магнитном поле с частотой  , то поток вектора магнитной индукции через поверхность, ограниченную контуром рамки, меняется со временем по закону:

,

где   – максимальное значение потока вектора индукции через плоскость контура. Возникающая при этом электродвижущая сила равна

.

Величина   называется амплитудой электродвижущей силы и представляет ее наибольшее значение.

Электродвижущая сила максимальна, когда угол  . В этом положении поток равен нулю, а скорость изменения магнитного потока максимальна. Когда  , поток максимален, а электродвижущая сила равна нулю. За один период электродвижущая сила дважды меняет знак. Периодически действующая электродвижущая сила вызывает в замкнутом проводнике переменный ток, также изменяющийся по периодическому закону.

Гармонически изменяющаяся электродвижущая сила – это идеализация. Такой закон изменения электродвижущей силы получается в том случае, когда магнитное поле однородно, а рамка вращается равномерно. Если хотя бы одно из этих условий нарушается, в контуре возникает электродвижущая сила, изменяющаяся по более сложному закону. Однако при равномерном вращении изменение электродвижущей силы происходит всегда по периодическому закону. Теория синусоидальных токов наиболее проста и хорошо разработана. Преимущество этого подхода подтверждается и тем, что все технические генераторы переменного тока имеют электродвижущую силу, изменяющуюся по синусоидальному закону. На этом основании при изучении переменных токов предпочтение отдается теории синусоидальных токов.

Активное и реактивное сопротивления

Сопротивление, оказываемое проходами и потребителями в цепях постоянного тока, называется омическим сопротивлением.

Если какой-либо проводник включить в цепь переменного тока, то окажется, что его сопротивление будет несколько больше, чем в цепи постоянного тока. Это объясняется явлением, получившим название скин-эффекта (поверхностный эффект).

Сущность его заключается в следующем. При прохождении переменного тока по проводнику внутри него существует переменное магнитное поле, пересекающее проводник. Магнитные силовые линии этого поля индуктируют в проводнике ЭДС, однако она будет не одинаковой в различных точках сечения проводника: к центру сечения на больше, а к периферии — меньше.

Это объясняется тем, что точки, лежащие ближе к центру, пересекаются большим числом силовых линий. Под действием этой ЭДС переменный ток будет распределяться не по всему сечению проводника равномерно, а ближе к его поверхности.

Это равносильно уменьшению полезного сечения проводника, а следовательно, увеличению его сопротивления переменному току. Например, медный провод длиной 1 км и диаметром 4 мм оказывает сопротивление: постоянному току - 1,86 ом, переменному частотой 800 гц - 1,87 ом, переменному току частотой 10000 гц - 2,90 ом.

Сопротивление, оказываемое проводником проходящему на нему переменному току, называется активным сопротивлением.

Если какой-либо потребитель не содержит в себе индуктивности и емкости (лампочка накаливания, нагревательный прибор), то он будет являться для переменного тока также активным сопротивлением.

Активное сопротивление зависит от частоты переменного тока, возрастая с ее увеличением.

Однако многие потребители обладают индуктивными и емкостными свойствами при прохождении через них переменного тока. К таким потребителям относятся трансформаторы, дроссели, электромагниты, конденсаторы, различного рода провода и многие другие.

При прохождении через них переменного тока необходимо учитывать не только активное, но и реактивное сопротивление, обусловленное наличием, в потребителе индуктивных и емкостных свойств его.

Известно, что если постоянный ток, проходящий по какой-либо обмотке, прерывать и замыкать, то одновременно с изменением тока будет изменяться и магнитный поток внутри обмотки, в результате чего в ней возникнет ЭДС самоиндукции.

То же самое будет наблюдаться и в обмотке, включенной в цепь переменного тока, с той лишь разницей, что здесьток непрерывно изменяется как по величине, так и по направлению. Следовательно, непрерывно будет изменяться величина магнитного потока, пронизывающего обмотку, и в ней будет индуктироваться ЭДС самоиндукции.

Но направление ЭДС самоиндукции всегда таково, что противодействует изменению тока. Так, при возрастании тока в обмотке ЭДС самоиндукции будет стремиться задержать нарастание тока, а при убывании тока, наоборот, будет стремиться поддержать исчезающий ток.

Отсюда следует, что ЭДС самоиндукции, возникающая в обмотке (проводнике), включенной в цепь переменного тока, будет всегда действовать против тока, задерживая его изменения. Иначе говоря, ЭДС самоиндукции можно рассматривать как дополнительное сопротивление, оказывающее вместе с активным сопротивлением обмотки противодействие проходящему через обмотку переменному току.

Сопротивление, оказываемое переменному току ЭДС самоиндукции, носит название индуктивного сопротивления.

Индуктивное сопротивление будет тем больше, чем больше индуктивность потребителя (цепи) и выше частота переменного тока. Это сопротивление выражается формулой xl = ωL, где xl - индуктивное сопротивление в омах; L - индуктивность в генри (гн); ω - угловая частота где f - частота тока).

Кроме индуктивного сопротивления существует емкостное сопротивление, обусловливаемое как наличием емкости в проводниках и обмотках, так и включением в отдельных случаях в цепь переменного тока конденсаторов. При увеличении емкости С потребителя (цепи) и угловой частоты тока емкостное сопротивление уменьшается.

Емкостное сопротивление равно xс = 1/ωС, где хс — емкостное сопротивление в омах, ω - угловая частота, С - емкость потребителя в фарадах.

Треугольник сопротивлений

Рассмотрим цепь, активное сопротивление элементов которой r, индуктивность L и емкость С. 

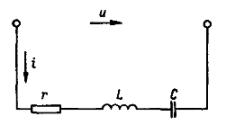Рис. 1. Цепь переменного тока с резистором, катушкой индуктивности и конденсатором.

Полное сопротивление такой цепи z = √r²+ (хl - xc)²) = √r² + x²)

Графически это выражение можно изобразить в виде, так называемого, треугольника сопротивлений.

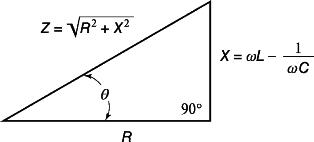Рис.2. Треугольник сопротивлений

Гипотенуза треугольника сопротивлений изображает полное сопротивление цепи, катеты — активное и реактивное сопротивления.

Если одно из сопротивлений цепи - (активное или реактивное), например, в 10 и более раз меньше другого, то меньшим можно пренебречь, в чем легко убедиться непосредственным расчетом.

Билет 33

Колебательный контур — осциллятор, представляющий собой электрическую цепь, содержащую соединённые катушку индуктивности и конденсатор. В такой цепи могут возбуждаться колебания тока (и напряжения).

Колебательный контур — простейшая система, в которой могут происходить свободные электромагнитные колебания

Резонансная частота контура определяется так называемой формулой Томсона: