Контур с током в магнитном поле

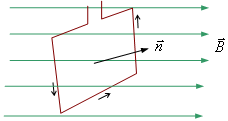Рис. 4.13

Пусть в однородное магнитное поле помещена рамка с током (рис. 4.13). Тогда силы Ампера, действующие на боковые стороны рамки, будут создавать вращающий момент, величина которого пропорциональна магнитной индукции, силе тока в рамке, ее площади S и зависит от угла a между вектором   и нормалью к площади  :

.

Направление нормали выбирают так, чтобы в направлении нормали перемещался правый винт при вращении по направлению тока в рамке.

Максимальное значение вращательный момент имеет тогда, когда рамка устанавливается перпендикулярно магнитным силовым линиям:

.

Это выражение также можно использовать для определения индукции магнитного поля:

.

Величину, равную произведению  , называют магнитным моментом контура Р_т. Магнитный момент есть вектор, направление которого совпадает с направлением нормали к контуру. Тогда вращательный момент можно записать

.

При угле a = 0 вращательный момент равен нулю. Значение вращательного момента зависит от площади контура, но не зависит от его формы. Поэтому на любой замкнутый контур, по которому течет постоянный ток, действует вращательный момент М, который поворачивает его так, чтобы вектор магнитного момента установился параллельно вектору индукции магнитного поля.

Вращающий момент (или момент силы)

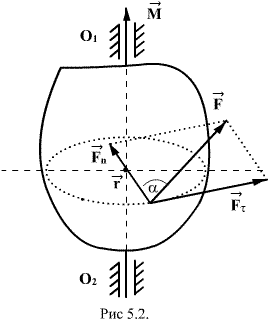
Пусть на тело, в плоскости перпендикулярной оси вращения   действует сила   (рис.5.2). Разложим эту силу на две составляющие:   и 

Сила   пересекает ось вращения и, следовательно, не влияет на вращение тела. Под действием составляющей   тело будет совершать вращательное движение вокруг оси  . Расстояние   от оси вращения до линии вдоль которой действует сила   называется плечом силы  . Моментом силы относительно точки О называется произведение модуля силы   на плечо 

С учетом, что 

момент силы

.

С точки зрения векторной алгебры это выражение представляет векторное произведение радиуса-вектора  , проведенного в точку приложения силы   на эту силу. Таким образом, момент силы относительно точки О является векторной величиной и равен

(5.1)

Вектор момента силы направлен перпендикулярно к плоскости, проведенной через векторы   и  , и образует с ними правую тройку векторов (при наблюдении из вершины вектора М видно, что вращение по кратчайшему расстоянию от   к   происходит против часовой стрелки).