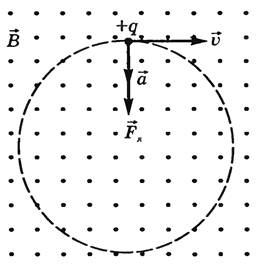
2. Заряженная частица движется перпендикулярно линиям магнитной индукции

тогда сила Лоренца   , следовательно, и сообщаемое ускорение будут постоянны по модулю и перпендикулярны к скорости частицы.

В результате частица будет двигаться по окружности , радиус которой можно найти на основании второго закона Ньютона:

   

Отношение       — называют удельным зарядом частицы.

  

Период вращения частицы

то есть период вращения не зависит от скорости частицы и радиуса траектории.

3. Скорость заряженной частицы направлена под углом к вектору.

  

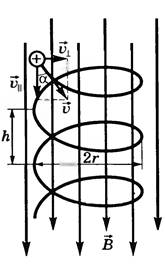
Движение частицы можно представить в виде суперпозиции равномерного прямолинейного движения вдоль поля со скоростью  и движения по окружности с постоянной по модулю скоростью  в плоскости, перпендикулярной полю.

Радиус окружности определяется аналогично предыдущему случаю, только надо   заменить  на    , то есть

В результате сложения этих движений возникает движение по винтовой линии, ось которой параллельна магнитному полю. Шаг винтовой линии

Направление, в котором закручивается спираль, зависит от знака заряда частицы.

Если скорость заряженной частицы составляет угол α с направлением вектора     неоднородного магнитного поля, индукция которого возрастает в направлении движения частицы, тο R и h уменьшаются с ростом B. На этом основана фокусировка заряженных частиц в магнитном поле.

Если на движущуюся заряженную частицу помимо магнитного поля с индукцией  действует одновременно и электростатическое поле с напряженностью , то равнодействующая сила, приложенная к частице, равна векторной сумме электрической силы и силы Лоренца:   . Характер движения и вид траектории зависят в данном случае от соотношения этих сил и от направления электростатического и магнитного полей.

Эффект Холла

Эффект, открытый американским физиком Эдвином Гербертом Холлом в 1879 году, заключается в явлении возникновения поперечной разности потенциалов в полупроводнике, по которому протекает электрический ток и существует магнитное поле Н, перпендикулярное направлению тока.

Физическая природа эффекта Холла заключается в том, что на движущийся носитель тока в магнитном поле с индукцией В действует сила Лоренца

, Н,                    (6.11)

где v –скорость носителя; q – его заряд.

Направление силы Лоренца определяется правилом левой руки. Если проводник n-типа проводимости, то электроны будут смещаться влево к внешней стороне пластины, заряжая её отрицательно (рис. 6.8).

В полупроводника p-типа проводимости при том же направлении тока сила Л оренца будет смещать дырки в том же направлении. При этом левая внешняя сторона пластинки зарядится положительно.

Если угол между вектором скорости носителей v  и вектором магнитной  индукции B равен 90^о, то величина силы Лоренца рассчитывается по формуле

F_л=qvB,                                                       (6.12)

где v – средняя дрейфовая скорость носителей заряда, м/c.

Электрическое поле  между поперечными гранями пластинки равно

, В/м,                                                  (6.13)

где U_х » (0,6…1)·10^-4 В - разность потенциалов между поперечными гранями пластинки, называемая эдс Холла; а – ширина пластинки.

 Поле Е_х действует на электроны с силой F=-qE_х, направленной против силы Лоренца F_л. При выполнении условия F_л=F поперечное электрическое поле уравновешивает силу Лоренца и дальнейшее накопление электрических зарядов на боковых гранях пластины прекращается. Тогда из равенстваqvB=qE_х следует E_х=vB. Дрейфовая скорость носителей тока определяется из выражения

,                                                          (6.14)

где j – плотность тока, А/м², n – концентрация электронов, м^-3,

Тогда выражение для  поля Е_х приобретает вид

.                                                    (6.15)

Умножив обе части равенства (6.15) на ширину пластинки а, получаем формулу для эдс Холла

, В.                                                    (6.16)

Формула (6.16) обычно записывается в виде

,                                                    (6.17)

где   – коэффициент Холла, м³/Кл.

С учетом разброса средней скорости дрейфа электронов в полупроводнике значение коэффициента Холла определяется из выражения

,                                             (6.18)

 где А=1,18 для полупроводников с преимущественным рассеянием носителей заряда на тепловых колебаниях кристаллической решетки; А=1,93 при рассеянии на ионизированных примесях.

Для дырочных полупроводников коэффициент Холла рассчитывается по формуле

  ,                                             (6.19)

где q и p –заряд и концентрация дырок, соответственно.

При смешенной электронно-дырочной проводимости величина коэффициента Холла рассчитывается по формуле

,                                             (6.20)

где μ_n и μ_p – подвижности электронов и дырок, соответственно.

Из формулы (6.20) следует, что в собственных полупроводниках при выполнении условия n_i=p_i значение коэффициента Холла равно

Билет 21

Закон Ампера устанавливает, что на проводник с током, помещенный в однородное магнитное поле, индукция которого В, действует сила, пропорциональная силе тока и индукции магнитного поля:

F = BIlsina (a - угол между направлением тока и индукцией магнитного поля ). Эта формула закона Ампера оказывается справедливой для прямолинейного проводника и однородного поля.

Если проводник имеет произвольную формулу и поле неоднородно, тоЗакон Ампера принимает вид:

dF = I*B*dlsina

Закон Ампера в векторной форме:

dF = I [dl B]

Сила Ампера направлена перпендикулярно плоскости, в которой лежат векторы dl и B.

Для определения направления силы, действующей на проводник с током, помещенный в магнитное поле, применяется правило левой руки.

Закон Ампера используется при нахождении силы взаимодействия двух токов. Рассмотрим два бесконечных прямолинейных параллельных тока I₁ и I₂; (направления токов даны на рис. 1), расстояние между которыми R. Каждый из проводников создает вокруг себя магнитное поле, которое действует по закону Ампера на соседний проводник с током. Найдем, с какой силой действует магнитное поле тока I₁ на элемент dl второго проводника с током I₂. Магнитное поле тока I₁ есть линии магнитной индукции, представляющие собой концентрические окружности. Направление вектора B₁ задается правилом правого винта, его модуль по формуле (5) есть    Направление силы dF₁, с которой поле B₁ действует на участок dl второго тока, находится по правилу левой руки и указано на рисунке. Модуль силы, используя (2), с учетом того, что угол α между элементами тока I₂ и вектором B₁ прямой, будет равен    подставляя значение для В₁, найдем   (3)  Аналогично рассуждая, можно показать, что сила dF₂ с которой магнитное поле тока I₂ действует на элемент dl первого проводника с током I₁, направлена в противоположную сторону и по модулю равна   (4)  Сопоставление выражений (3) и (4) дает, что    т. е. два параллельных тока одинакового направления притягиваются друг к другу с силой, равной   (5)  Если токи имеют противоположные направления, то, используя правило левой руки, определим, что между ними действует сила отталкивания, определяемая выражением (5).  Рис.1

Билет 20